Dev.C++树状数组模板:简单来说,线段树能做的,树状数组不一定能做;树状数组能做的,线段树一定能做,但是做的极少有比他好。
#include<bits/stdc++.h>
#define MAXN 500500
using namespace std;
int a[MAXN],c[MAXN],n,m;//数组有n个数,有m条指令
int lowbit(int x)return x&-x;
void update(int x,int y)//将第x项变成y(或者加减等运算)
{
while(x<=n)//不能越界
{
c[x]+=y;//or c[x]-=y等等
x+=lowbit(x);//玄学操作
}
}
void getsum(int x)//求和(从第一项加到第x项)
{
int sum=0,tmp=x;
while(tmp!=0)
{
sum+=c[tmp];//加上沿途所有值
tmp-=lowbit;//玄学操作
}
}
嘿嘿,这次***偷个小懒,就不发主函数部分了,这个有脑子的人都会打这个取决于题目。
老板:骂老板!扣工资!
这次的解析分为四部分:玄学操作,单点修改,单点和区间查询及区间修改。
一:玄学操作
树状数组最重要的玄学操作叫做捞比特lowbit。lowbit翻译过来就是最低比特位。他的代码很简单:
x & -x
简单吧。接下来,我将详细介绍它的原理及作用。
首先,这个原理纯粹就是前人的智慧。这里利用的负数的存储特性,负数是以补码存储的,对于整数运算x&(−x)有
-
当x为0时,即 0&0,结果为0;
-
当x为奇数时,最后一个比特位为1,取反加1没有进位,故x和−x除最后一位外前面的位正好相反,按位与结果为0。结果为1。
-
当x为偶数,且为2的m次方时,x的二进制表示中只有一位是1(从右往左的第m+1位),其右边有m位0,故x取反加1后,从右到左第有m个0,第m+1位及其左边全是1。这样,x&(−x) 得到的就是x。
-
当x为偶数,却不为2的m次方的形式时,可以写作x=y∗(2k)。其中,y的最低位为1。实际上就是把x用一个奇数左移k位来表示。这时,x的二进制表示最右边有k个0,从右往左第k+1位为1。当对x取反时,最右边的k位0变成1,第k+1位变为0;再加1,最右边的k位就又变成了0,第k+1位因为进位的关系变成了1。左边的位因为没有进位,正好和x原来对应的位上的值相反。二者按位与,得到:第k+1位上为1,左边右边都为0。结果为2k。
总结一下:x&(−x),当x为0时结果为0;x为奇数时,结果为1;x为偶数时,结果为x中2的最大次方的因子。
请问,你记住了吗?没记住没关系,我也没记住只用记住lowbit是用来查询上下级关系的就ok
因为树状数组是一个这样的结构
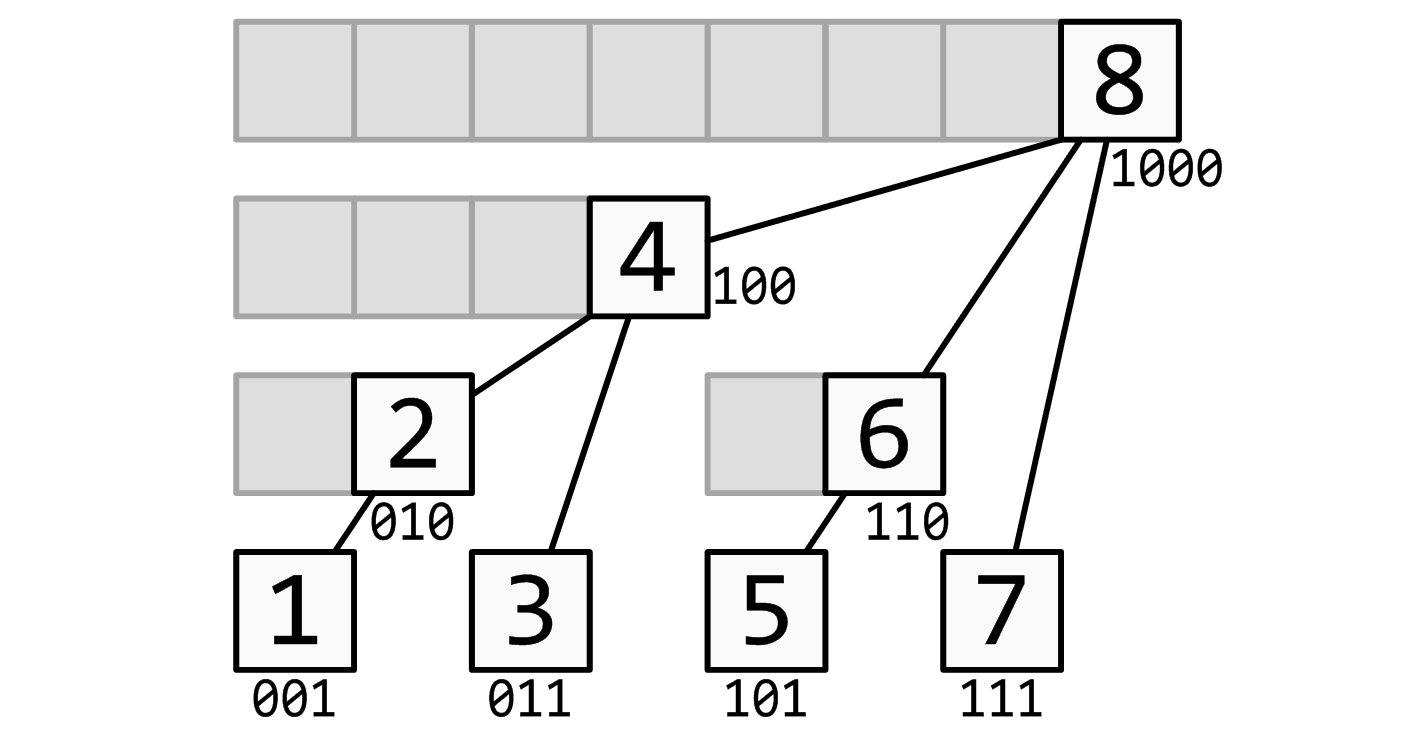
这个结构的思想和线段树(不知道线段树的戳这)有些类似:用一个大节点表示一些小节点的信息,进行查询的时候只需要查询一些大节点而不是更多的小节点。
最下面的八个方块就代表存入a中的八个数,现在都是十进制。
他们上面的参差不齐的剩下的方块就代表a的上级——c数组。
很显然看出:
c2管理的是a1&a2;
c4管理的是a1&a2&a3&a4;
c6管理的是a5&a6;c8则管理全部8个数。
那么问题来了,你是怎么知道c管的a的个数分别是多少呢?你那个1个,2个,3个……是怎么来的呢?你看看,再看看捞比特,哦~~
没看懂
不,你一定看懂了!这个捞比特算出来的正好是他所管理的数的个数。
看似高深,其实简单。说着简单,用着……emmmm!

二:单点修改
单点修改并不难,所以我们很快就过了。
单点修改只需要更改你所需要更改的单点,再利用捞比特依次将他的上级修改了就OK。
一边循环就能过。
void update(int x,int y)//将第x项变成y(或者加减等运算)
{
while(x<=n)//不能越界
{
c[x]+=y;//or c[x]-=y等等
x+=lowbit(x);//玄学操作
}
}
猝不及防的代码
三:单点和区间查询
查询的话真的是很……会了单点真的就会了区间
要学会查询,首先得会从第一项加到第x项。只用从第x向下加捞比特,加到x=0时,从第一项到第x项就加完了。
代码:
void getsum(int x)//求和(从第一项加到第x项)
{
int sum=0,tmp=x;
while(tmp!=0)
{
sum+=c[tmp];//加上沿途所有值
tmp-=lowbit;//玄学操作
}
}
至于单点,例如我要查x的值,就用getsum(x)(从第一项加到第x项)-(减去) getsum(x-1)(从第一项加到第x-1项)就可以了,区间查询也一样。怎么样,是不是特简单?
四:区间修改
说实话,树状数组真的不适合打区间修改,但是,如果打成了,那比线段树强多了。我也是研究了好久,主要是难理解,如果你想背模板那就背吧。
树状数组的区间修改要用树状数组维护另一个数组,利用这个数组来维护原数组,比较麻烦,代码我就不贴了。
五:注意事项
记牢了!
单点修改不能和区间查询一起用
区间修改不能和单点查询一起用
不要问我为什么
大佬zhnzh告诉我的不解释~