一、引言
B树是二叉平衡树的一个变种,在学习之前,我们先了解一下二分法,二叉树的一些相关的基本概念,有助于我们更好的理解B树~
二、二叉树
定义:二叉树即二叉平衡树
意义:通过二分法来进行元素查找,时间复杂度为O(logn)
查找元素的流程:
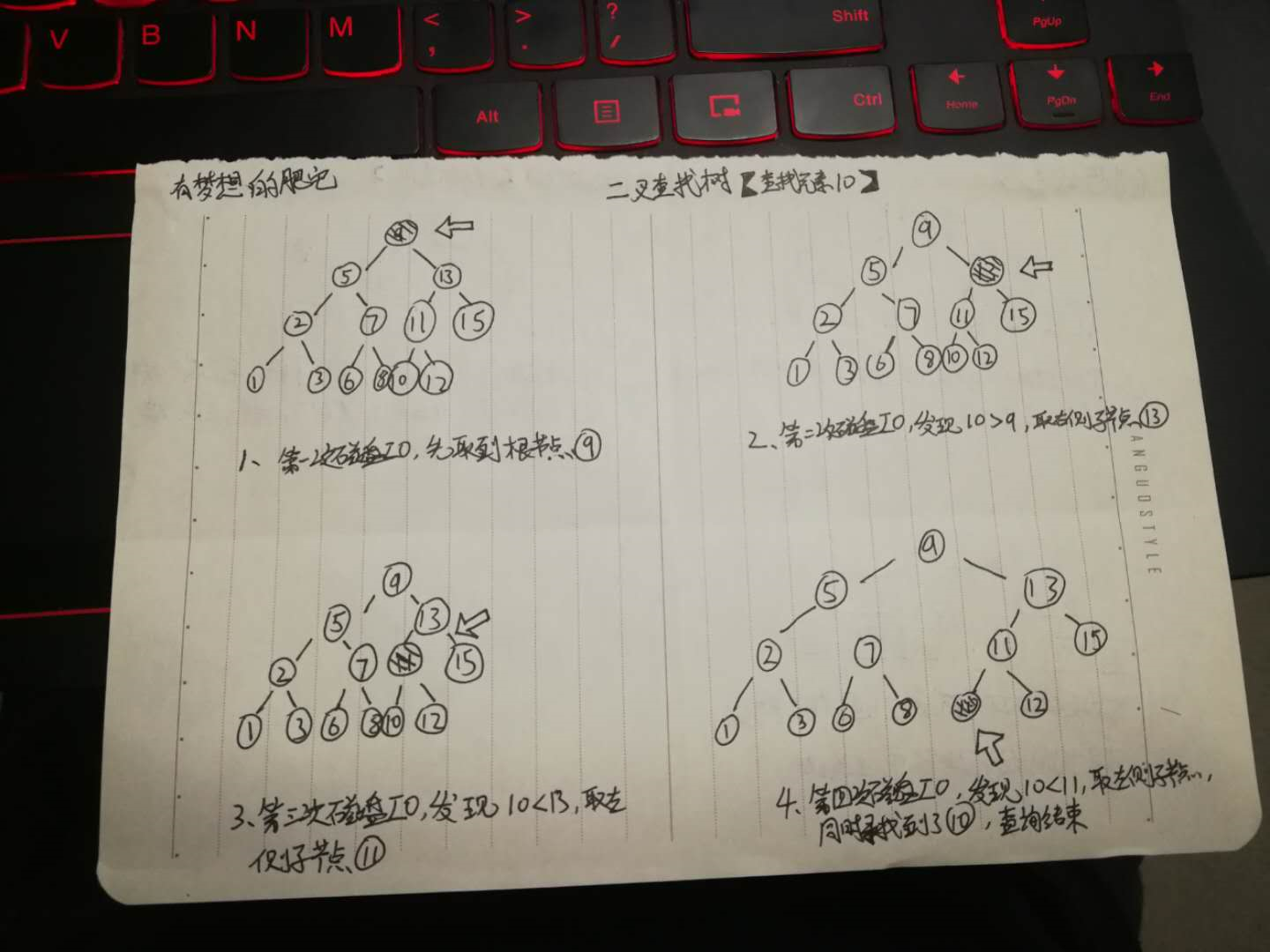
解析:我们可以通过上图(画功有限,请见谅...)看到,二叉树具有以下几个特征:
- 非叶子节点都有2个分支【非叶子节点2个孩子】
- 左侧分支的值比右侧分支的元素要小【左小右大】
- 查询元素时通过与当前节点元素进行比较大小,若小于当前节点的元素走左侧分支,大于当前节点的元素时,则走右侧分支【查询时,小于走左边,大于走右边】
优势:
- 若非最悲观的情况(即查到最后一层)或者查询的层数不高的时候,可以比较快的返回相应的元素(但通常这个查询深度不可控,因为不确定查的元素在第几层)
- 每一个节点都存有对应的元素,若获取的元素正好在当前节点时,则不再继续往下走了,磁盘IO就会少一些。
劣势:
当查询深度较高时,会增加磁盘IO的次数,影响效率(图中以每取一次节点进行一次磁盘IO为例)
三、B树
定义:B树即多路平衡查找树
常见应用:文件系统和部分非关系型数据库的索引,如MongoDB
优势:树用作数据库索引主要是因为查询效率高,而且可以保持有序
查找元素的流程:

原则:一个m阶的B树(Balance Tree)具有如下几个特征:
- 1、根结点至少有两个子女。
- 2、每个中间节点都包含k-1个元素和k个孩子,其中 m/2 <= k <= m
- 3、每一个叶子节点都包含k-1个元素,其中 m/2 <= k <= m
- 4、所有的叶子结点都位于同一层。
- 5、每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划。
解析:我们可以对着上面的原则进行解析,图中是一个3阶的B树,那么m为3,m/2 <= k <= m则k可以取2,3,k-1就是1,2了。
- 1、根结点至少有两个子女【根节点是9,有2个子女】
- 2、每个中间节点都包含k-1【1~2】个元素和k【2~3】个孩子,其中 m/2 <= k <= m,满足
- 3、每一个叶子节点都包含k-1【1~2】个元素,其中 m/2 <= k <= m
- 4、所有的叶子结点都位于同一层。
- 5、每个节点中的元素从小到大排列,节点当中k-1【1~2】个元素正好是k【2~3】个孩子包含的元素的值域分划。
优势:
- 存放同样多的元素时,树的高度变小了,相当于减少了磁盘IO次数,提升性能
- 当查询进入了一个有很多元素的节点时,也只是存在于内存中进行比较,相对于磁盘IO的速度来说,消耗的时间可以忽略不计【这也是为什么在节点上进行“扩容”】
劣势:
- 相对于B+树来说,每个节点都会存数据,同样大小的磁盘页存的节点元素会少些
- 查询性能不稳定,比如有时可能会查到底层的叶子节点,有时可能查到最上层的根节点就返回了,每次查询的消耗不稳定,查询耗时波动大。
- 范围查询不方便,比如图中我要查询符合6~10的所有元素,而6~10的元素从根节点开始就分布在2侧的树中,所以需要经过的中序遍历非常繁杂
参考资料: