1.AtCoder Beginner Contest 207 D.Congruence Points

大意:给出两个集合,能否通过旋转和平移A集合中的点使它们与B集合中的点完全重合?
题解:找出每个集合的重心,然后将重心移动到原点,那么就只需要考虑能否通过旋转使他们重合。找到A集合和B集合中到原点距离相等的两个点,求出需要旋转的角度,再暴力将A集合中的每个点旋转,判断是否能与B集合完全重合。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=120; const double esp=1e-9; int n,na,nb; int a[maxn],b[maxn],c[maxn],d[maxn]; int x,y,xx,yy,sum; double pf(double x){ return x*x; } int main(){ cin>>n; for(int i=1;i<=n;i++){ cin>>a[i]>>b[i]; a[i]*=n; b[i]*=n; } for(int i=1;i<=n;i++){ cin>>c[i]>>d[i]; c[i]*=n; d[i]*=n; } for(int i=1;i<=n;i++) sum+=a[i]; x=sum/n; sum=0; for(int i=1;i<=n;i++) sum+=b[i]; y=sum/n; sum=0; for(int i=1;i<=n;i++) sum+=c[i]; xx=sum/n; sum=0; for(int i=1;i<=n;i++) sum+=d[i]; yy=sum/n; sum=0; for(int i=1;i<=n;i++){ a[i]-=x; b[i]-=y; c[i]-=xx; d[i]-=yy; if(a[i]!=0){ na=a[i];nb=b[i]; } } for(int i=1;i<=n;i++){ if(fabs(pf(c[i])+pf(d[i])-pf(na)-pf(nb))<=esp){ double ang=atan2(d[i],c[i])-atan2(nb,na); bool p=1; for(int j=1;j<=n;j++){ double nowa=a[j]*cos(ang)-b[j]*sin(ang); double nowb=a[j]*sin(ang)+b[j]*cos(ang); bool v=0; for(int k=1;k<=n;k++){ if(fabs(nowa-c[k])<=esp&&fabs(nowb-d[k])<=esp){ v=1; break; } } p&=v; } if(p){ cout<<"Yes"<<endl; return 0; } } } cout<<"No"<<endl; return 0; }
2.AtCoder Beginner Contest 207 E.Mod i

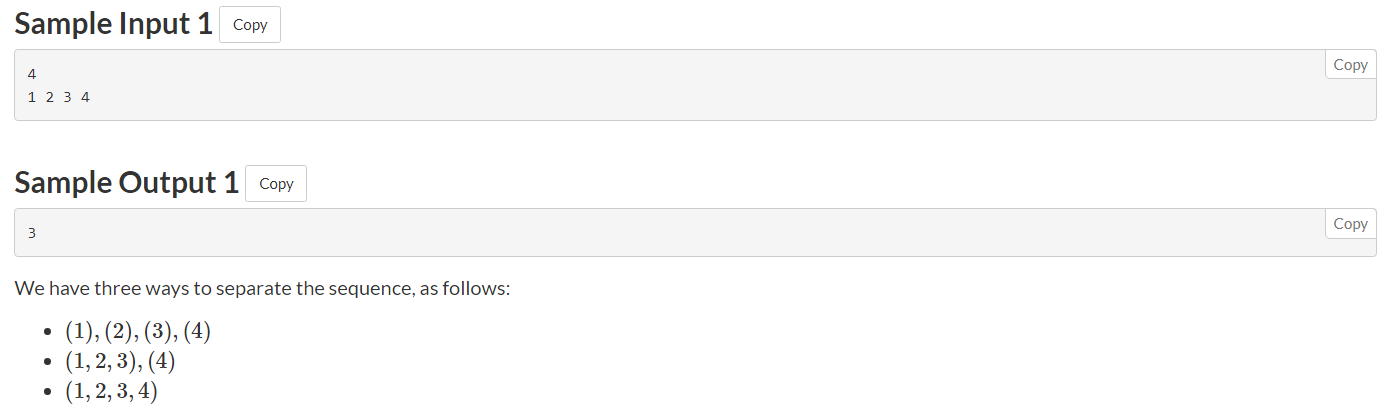
大意:把给定的数组分为 k 段,满足第 i 段的和被 i 整除,求方案数。
题解:设dp[ i ][ j ] 为前 i 个数分成 j 个区间的方案数,则 dp[ i ][ j ] += dp[ k ][ j-1 ] , 满足 1≤ k < i 且 ( sum[ i ] - sum[ k ] )% j ==0 。显然复杂度是O(n3),考虑优化,可以发现若( sum[ i ] - sum[ k ] )% j ==0,则 sum[ i ] % j == sum[ k ] % j,令num[ sum[ i ]%j ][ j-1 ] 为 dp[ k ][ j-1 ] 的和,则 dp[ i ][ j ] = num[ sum[ i ]%j ][ j-1 ],复杂度为O(n²)。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=3020; const int mod=1e9+7; ll n,a[maxn],dp[maxn][maxn],sum[maxn],num[maxn][maxn]; int main(){ cin>>n; for(int i=1;i<=n;i++){ cin>>a[i]; sum[i]=sum[i-1]+a[i]; } num[0][0]=1; for(int j=1;j<=n;j++) for(int i=j-1;i<=n;i++){ dp[i][j]=num[sum[i]%j][j-1]; num[sum[i]%j][j-1]=(num[sum[i]%j][j-1]+dp[i][j-1])%mod; } ll ans=0; for(int i=1;i<=n;i++) ans=(ans+dp[n][i])%mod; cout<<ans<<endl; return 0; }
3.AtCoder Beginner Contest 214 D.Sum of Maximum Weights

大意:给出一棵树以及它每条边的边权,定义f( i, j )为点 i 到 j 之间最短路径所经过的边权的最大值,求上式的值。
题解:把所有边按权值从小到大排序,按最小生成树的做法,每次合并两个点的时候,答案加上左边集合的大小*右边集合的大小*当前边的边权。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=1e5+50; const int maxm=2e5+50; int n,fat[maxn],sum[maxn]; ll ans; struct node{ int x,y,z; }a[maxn]; int cmp(const node &a,const node &b){ return a.z<b.z; } int father(int x){ if(x!=fat[x]) fat[x]=father(fat[x]); return fat[x]; } template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>n; for(int i=1;i<=n;i++){ fat[i]=i; sum[i]=1; } for(int i=1;i<n;i++){ read(a[i].x),read(a[i].y),read(a[i].z); } sort(a+1,a+n,cmp); for(int i=1;i<=n-1;i++){ int fa=father(a[i].x),fb=father(a[i].y); if(fa!=fb){ ans+=1ll*sum[fa]*sum[fb]*a[i].z; fat[fa]=fb; sum[fb]+=sum[fa]; } } cout<<ans; return 0; }
