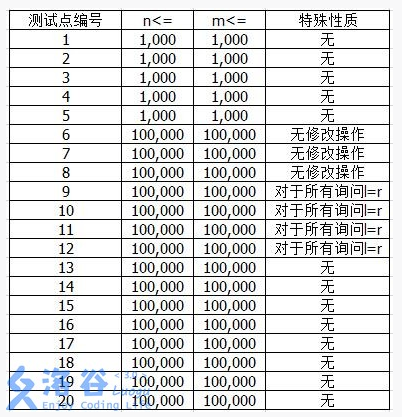
题目描述
从家到学校之间有n段路连成一条直线,每一段路有一个湿滑度si,表示走在这段路上就会有si的概率摔倒。由于雨下得比较大,所以政府也出动了不少人力减少道路的湿滑度。每次政府的操作可以表示成1 l r t,表示把区间[l,r]上所有道路的湿滑度乘以t。
但是小W还是很担心,因此他经常会询问你,在一个区间的道路上行走不摔倒的概率是多少。
输入
第一行两个正整数,为n,m,表示道路的数量以及操作的数量。
接下来1行有n个实数,为初始时道路的si。
接下来m行每行要么是1 l r t,表示把[l,r]中道路的湿滑度同时乘以t;要么是0 l r,表示询问从第l段路走到第r段路不摔倒的概率。
输出
对于每个询问操作,输出一行,表示不摔倒的概率。四舍五入到6位小数,你的输出必须和标准答案一模一样才可以得分。
样例输入
4 5 0.1 0.2 0.3 0.4 0 1 3 1 1 2 0.5 0 1 4 1 3 4 0.4 0 2 4
样例输出
0.504000 0.359100 0.665280
题解
考虑如何计算结果。假定结果为
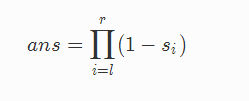
乘法不好计算,考虑取对数函数
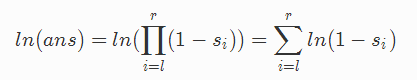
注意到自然对数的泰勒展开式,我们有
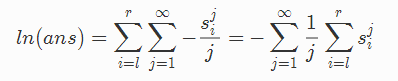
根据题目的条件,我们会发现后面那个求和部分随j的增大迅速减小,而题目只要求保留到6位精度,因此j最大取到20已经足够了(当然,在考场上最好还是取稍微大一点把稳一点)。
于是我们可以开一棵线段树,每个节点上维护20个值,分别表示不同的 j 下 的值。于是这道题就完美地解决了,复杂度O(20nlogn)
的值。于是这道题就完美地解决了,复杂度O(20nlogn)