开始总以为网络流是多么高深的东西,一直不敢去接受,然而学完以后发现好像也不是太难哦,只是好多基础东西的一些整合。
文章中可能会有多出纰漏,敬请读者不吝赐教。
我们以一个经典的问题引入算法。
你所在的村庄新开通了地下流水管道,自来水厂源源不断的提供水,村民们用水直接或间接用水,而村庄用完的废水统一回收于另一点(设排来的水全部回收)。当然每个管道有一定的容量,废水站求出最多可以汇聚多少水?
当然这是一个有向图。

首先明确几个概念:
容量:每条边都有一个容量(水管的最大水流容量)
源点:出发点(水厂)。
汇点:结束点(废水站)。
流:一个合法解称作一个流,也就是一条可以从源点到汇点的一条合法路径。
流量:每条边各自被经过的次数称作其流量,最终收集的总数为整个流的流量。
图中会有这么几个限制:
容量限制:每条边的流量不超过其容量(水管会爆的)。
流量平衡:对于除源点和汇点以外的点来说,其流入量一定等于流出量。
现在,我们先简化一下这个图,来解决这个问题。
x/y表示总流量为y,已经流了x.
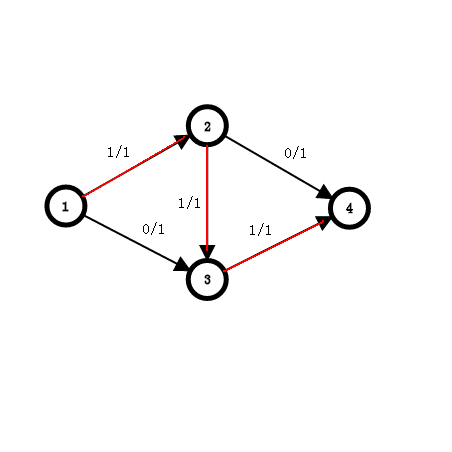
首先我们会想到,随机找路径,然而如果走到如上图所示。
当走完,1->2->3->4我们就找不到其他路径了,那么答案为1吗?不答案为2.
现在我们改进算法,给流过的路径建反向边,像这样:
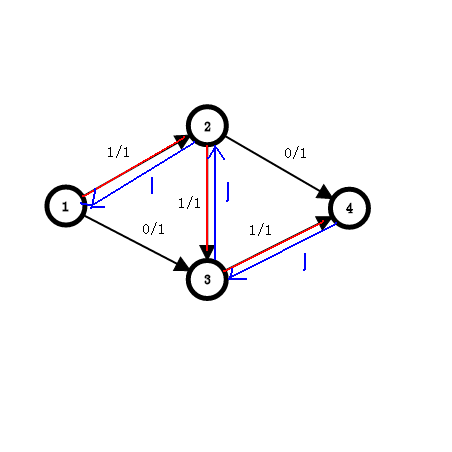
给程序有反悔的机会。
定义一跳变得残量为:容量 - 已流过的流量。
反向边的流量值=正向流过的总流量,也就是说正向流过多少,反向可以流回多少。
从而我们又找到1->3->2->4的一条路径。
再次建路径上的反向边,我们发现没有路径可以到达4点,所以答案为2.
小结:
总结一下上面求最大流的步骤:
1.在图上找到一条从源点到汇点的路径(称为‘增广路’)。
2.去增广路上的残量最小值v。(也就是流过的路径中流量最小的那一个)
3.将答案加上v。
4,.将增广路上所有边的残量减去v,反向边的残量加上v。
重复上边4个步骤直到找不到增光路为止,这称作 FF 方法。
算法的正确性一会进行证明,我们先看一下这个算法的效率。
首先这个算法应定不会死循环的,应为每次增广都会导致流量增加(并且增加的是整数),而且流量有一个客观存在最大值,所以它必定结束。(不理解不重要啦QAQ)
由于我们并没有指定它走哪一条边,所以优先考虑随便走一条边。
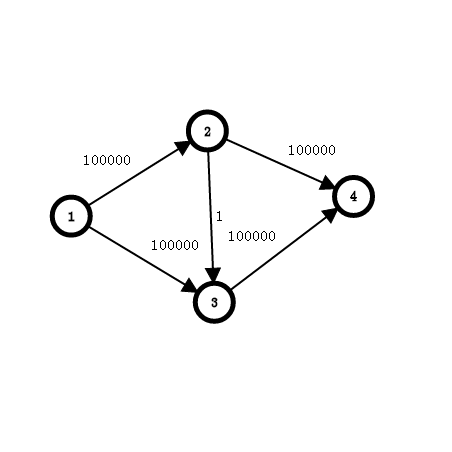
我们考虑一种极限的情况:
现增广1->2->3->4,会出现一条3->2容量为1的边。
再增广1->3->2->4,再增广1->2->3->4....
这浪费大量的时间,如果脸黑的话最多200000次。
然而我们如果先1->2->4,然后1->3->4,走两次就好了,上面的做法是我们不期望的。
我们可以考虑每次增广最短路。
EK算法:
EK算法是以上算法的实现:每次寻找最短路进行增广。
时间复杂度$O(m2n)$
首先我们定义几个数组以及变量:
结构体:储存三个变量,nxt,to,dis [邻接表建边]
flow[ i ] :表示流过 i 点的 v 值,也就是说目前经过到 i 点的路径上的最小的残量。
dis[ i ]:表示 i 点距离源点的距离,S,T表示源点以及汇点。
明确一个观点:
位运算符 ^ :1^1=0 0^1=1 2^1=3 3^1=2.
可以大致明白它的运算效果。
代码推演:
建边的时候,为了方便 ^ 运算符使用,我们可以提前建好反向边,之后一条边,^ 一下就是另一条边了。
首先我们利用bfs处理图的连通性以及所有点与源点的距离,当然,当这条边上的残量已经为0的时候,我们他已经不能经过,我们可以直接不考虑。
在bfs中pre数组是记录每个点最短路的前驱,last数组记录上条边的编号,从而记录出最短路径,然后从汇点进行更新即可。
bool bfs(int s,int t) { memset(flow,0x7f,sizeof(flow)); memset(dis,0x7f,sizeof(dis)); memset(vis,0,sizeof(vis)); Q.push(s);vis[s]=1;dis[s]=0,pre[t]=-1; while(!Q.empty()) { int temp=Q.front(); Q.pop(); vis[temp]=0; for(int i=head[temp];i!=-1;i=edge[i].nxt) { int v=edge[i].to; if(edge[i].flow>0&&dis[v]>dis[temp]+edge[i].dis) { dis[v]=dis[temp]+edge[i].dis; pre[v]=temp; last[v]=i; flow[v]=min(flow[temp],edge[i].flow); if(!vis[v]) { vis[v]=1; Q.push(v); } } } } return pre[t]!=-1; }
从汇点向前更新。
while(bfs(s,t)) { int now=t; maxflow+=flow[t]; mincost+=flow[t]*dis[t]; while(now!=s) { edge[last[now]].flow-=flow[t]; edge[last[now]^1].flow+=flow[t]; now=pre[now]; } }
EK算法还能优化么?
在此之前我们先了解一个定理:.
最大流最小割定理
什么是割?
这么来说吧,有个人住在废水收集站站附近,他不想然人们江水流到那,晚上偷偷在某个管道处切了一刀,图成为不联通的两块,从没有水流源点流到汇点。
选出一些管道,切断以后,图不连通,这些管道的集合就叫割。
这些边的容量之和叫做这个割的容量。
任取一个割,其容量大于最大流的流量,why?
从源点到汇点每次都会经过割上的最少一条边。
割掉这条边以后把源点能到达的边放在左边,不能到达的放在右边。
显然源点到会点的流量不会超过从左边走向右边的次数,而这又不会从左边到右边的容量之和。、
直观一点:
当n管道在一起的时候,你一刀全部切断,不在一起的时候你也不至于切n+1刀吧。
最小割的容量等于最大流的流量
这个定理如何证明呢?
■考虑FF算法时,残量网络上没有了增广路。
那么我们假设这时候,从源点经过残量网络能到达的点组成的集合为$X$,不能到达的点为$Y$。显然汇点在$Y$里,并且残量网络上没有从$X$到$Y$的边。
可以发现以下事实成立:
1.$Y$到$X$的边的流量为0.如果不为0,那么一定存在一条从X到Y的反向边,于是矛盾。
2.$X$到$Y$的边流量等于其容量。只有这样它才不会在残量网络中出现。
■根据第一个条件得知:没有流量从$X$到$Y$后又回到$X$。所以当前流量应该等于从$X$到$Y$的边的流量之和,而根据第二个条件他又等于$X$到$Y$的边容量之和。
■而所有从X到Y的边又构成了一个割,其容量等于这些边的容量之和。
★这意味着我们找到一个割和一个流,使得前者的流量等于后者的容量。而根据前边的结论,最大流的流量不超过这个割的容量,所以这个流一定是最大流。
■同样的,最小割的容量也不会小于这个流的流量,所以这个割也一定是最小割。
■而这也正是FF方法的最后局面,由此我们对出结论:
FF是正确的,并且最小割等于最大流
(据说还可以通过线性规划对偶定理证明 ...orz)
EK优--Dinic
EK时间复杂度太高,虽然大多数情况跑不到上界。
有一个显然的优化:
如果增广一次后发现最短路没有变化,那么可以继续增广,直到源点到汇点的增广路增大,才需要一边bfs。
bfs之后我们去除那些可能在最短路上的边,即dis[终点]=dis[起点]+1的那些边。
显然这些边构成的图中没有环。
我们只需要延这些边尽可能的增广即可。
实现:
bfs处直接上代码,比较简单。
int bfs() { memset(dis,-1,sizeof(dis)); dis[S]=0; Q.push(S); while(!Q.empty()) { int u=Q.front(); Q.pop() ; for(int i=head[u];i!=-1;i=edge[i].nxt) { int v=edge[i].to; if(dis[v]==-1&&edge[i].w>0) { dis[v]=dis[u]+1; //更新 Q.push(v); } } } return dis[T]!=-1; //判断是否联通。 }
dfs:
当图联通时进行dfs,目前节点为u,每次经过与u距离最近的点,并且这条边的残量值要大于0,然后往后进行dfs。
我们在dfs是要加一个变量,作为流量控制(后边的流量不能超过前边流量的最小值)。
dfs中变量flow记录这条管道之后的最大流量。
bool dfs(int u,int exp) { if(u==T)return exp; //到达重点,全部接受。 int flow=0,tmp=0; for(int i=head[u];i!=-1;i=edge[i].nxt) { int v=edge[i].to; //下一个点。 if(dis[v]==dis[u]+1&&edge[i].w>0) { tmp=dfs(v,min(exp,edge[i].w)); //往下进行 if(!tmp)continue; exp-=tmp; //流量限制-流量,后边有判断。 flow+=tmp; edge[i].w-=tmp; //路径上的边残量减少 edge[i^1].w+=tmp; //流经的边的反向边残量增加。 if(!exp)break; //判断是否在限制边缘 } } return flow; }
重复上边如果图联通(有最短路径),就一直进行增广。
while(bfs())ans+=dfs(S,inf);
时间复杂度:
Dinic复杂度可以证明是$O(n2m)$
在某些特殊情况下(每个点要么只有一条入边且容量为1,要么仅有一条出边且容量为1)其时间复杂度甚至能做到$O(m sqrt n )$

#include <iostream> #include <cstring> #include <cstdio> #include <queue> using namespace std; #define inf 0x7fffffff int head[10010],tot; struct ahah{ int nxt,to,w; }edge[100010]; void add(int x,int y,int z) { edge[tot].nxt=head[x]; edge[tot].to=y; edge[tot].w=z; head[x]=tot++; } int n,m,x,y,z; int ans,flow; int dis[10010]; queue <int> Q; int S,T; int bfs() { memset(dis,-1,sizeof(dis)); dis[S]=0; Q.push(S); while(!Q.empty()) { int u=Q.front(); Q.pop() ; for(int i=head[u];i!=-1;i=edge[i].nxt) { int v=edge[i].to; if(dis[v]==-1&&edge[i].w>0) { dis[v]=dis[u]+1; //更新 Q.push(v); } } } return dis[T]!=-1; //判断是否联通。 } bool dfs(int u,int exp) { if(u==T)return exp; //到达重点,全部接受。 int flow=0,tmp=0; for(int i=head[u];i!=-1;i=edge[i].nxt) { int v=edge[i].to; //下一个点。 if(dis[v]==dis[u]+1&&edge[i].w>0) { tmp=dfs(v,min(exp,edge[i].w)); //往下进行 if(!tmp)continue; exp-=tmp; //流量限制-流量,后边有判断。 flow+=tmp; edge[i].w-=tmp; //路径上的边残量减少 edge[i^1].w+=tmp; //流经的边的反向边残量增加。 if(!exp)break; //判断是否在限制边缘 } } return flow; } int main() { memset(head,-1,sizeof(head)); scanf("%d%d%d%d",&n,&m,&S,&T); for(int i=1;i<=m;i++) { scanf("%d%d%d",&x,&y,&z); add(x,y,z);add(y,x,0); //相邻建边。 } while(bfs())ans+=dfs(S,inf); printf("%d",ans); }
当前弧优化:
这优化我也不是太熟悉啦。
当前弧优化的意思就是说每次开始跑邻接表遍历不是从第一条边开始跑而是从上一次点i遍历跑到的点.
我们用cur[i]表示这个点,之后每次建完分层图之后都要进行初始化,且见分层图时不存在当前弧优化.

int deep[N+1]; int q[N+1]= {0},h,t; int cur[N+1]; bool bfs(int S,int T) { for (int i=0; i<=n; i++) deep[i]=0; //初始化深度为0 h=t=1; q[1]=S; deep[S]=1; while (h<=t) { for (int i=lin[q[h]]; i; i=e[i].next) if (!deep[e[i].y]&&e[i].v) //若未计算过深度且这条边不能是空的 { q[++t]=e[i].y; //入队一个节点 deep[q[t]]=deep[q[h]]+1; //计算深度 } ++h; } if (deep[T]) return true; else return false; } int dfs(int start,int T,int minf) { if (start==T) return minf; //若到了汇点直接返回前面流过来的流量 int sum=0,flow=0; for (int &i=cur[start]; i; i=e[i].next) //当前弧优化,运用指针在修改i的同时,将cur[start]顺便修改 if (e[i].v&&deep[start]+1==deep[e[i].y]) { flow=dfs(e[i].y,T,min(minf,e[i].v)); //继续找增广路 if (!flow) deep[e[i].y]=0; //去掉已经增广完的点 sum+=flow; //统计最大流 minf-=flow; //剩余容量 e[i].v-=flow; e[i^1].v+=flow; //更新剩余容量 if (!minf) return sum; //若前面已经流完了,直接返回 } return sum; //返回最大流量 } int maxflow(int S,int T) { int sum=0,minf; while (1) //while(1) 控制循环 { if (!bfs(S,T)) return sum; //bfs求出分层图,顺便判断是否有增广路 for (int i=1; i<=n; i++) cur[i]=lin[i]; //当前弧的初始化 minf=dfs(S,T,INF); //dfs求出流量 if (minf) sum+=minf; //若流量不为0,加入 else return sum; //流量为0,说明没有增广路,返回最大流 } }
