POJ-1661 Help Jimmy (DP)

Description

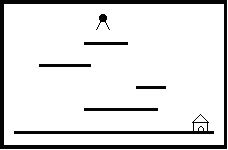
"Help Jimmy" 是在下图所示的场景上完成的游戏。

场景中包括多个长度和高度各不相同的平台。地面是最低的平台，高度为零，长度无限。

Jimmy老鼠在时刻0从高于所有平台的某处开始下落，它的下落速度始终为1米/秒。当Jimmy落到某个平台上时，游戏者选择让它向左还是向右跑，它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时，开始继续下落。Jimmy每次下落的高度不能超过MAX米，不然就会摔死，游戏也会结束。

设计一个程序，计算Jimmy到底地面时可能的最早时间。

Input

第一行是测试数据的组数t（0 <= t <= 20）。每组测试数据的第一行是四个整数N，X，Y，MAX，用空格分隔。N是平台的数目（不包括地面），X和Y是Jimmy开始下落的位置的横竖坐标，MAX是一次下落的最大高度。接下来的N行每行描述一个平台，包括三个整数，X1[i]，X2[i]和H[i]。H[i]表示平台的高度，X1[i]和X2[i]表示平台左右端点的横坐标。1 <= N <= 1000，-20000 <= X, X1[i], X2[i] <= 20000，0 < H[i] < Y <= 20000（i = 1..N）。所有坐标的单位都是米。

Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘，被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。

Output

对输入的每组测试数据，输出一个整数，Jimmy到底地面时可能的最早时间。

Sample Input

1
3 8 17 20
0 10 8
0 10 13
4 14 3

Sample Output

23

---

 

思路：

• 竖直方向的距离是不变的，因此只用讨论水平方向的距离；
• 将平台的高度从小到大排序，起点设为n+1个平台，设dp(i, 0), dp(i, 1)为到达第i个平台左、右边的最短路径；
• 从下往上递推即可得到最优解min{dp(n+1, 0), dp(n+1, 1)} + y；

---

Code:

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;
const int MAXN = 1000 + 10;
int dp[MAXN][2];

struct node {
    int h, l, r;
}a[MAXN];

bool cmp(node a, node b) {
    return a.h < b.h;
}

int main() {
    std::ios::sync_with_stdio(false);
    int T, n, maxh, x, y;
    cin>>T;
    while(T--) {
        memset(dp, 0x3f, sizeof(dp));
        cin>>n>>x>>y>>maxh;
        for (int i = 1; i <= n; ++i)
            cin>>a[i].l>>a[i].r>>a[i].h;
        a[0].h = 0;
        a[n+1].l = a[n+1].r = x;
        sort(a, a+1+n, cmp);
        for (int i = 1; i <= n+1; ++i) {
            bool flag1 = 0, flag2 = 0;
            for (int j = i - 1; j >= 0 && a[i].h - a[j].h <= maxh; --j) {
                if (flag1 && flag2) break;
                if (j == 0) {
                    if (!flag1) dp[i][0] = 0;
                    if (!flag2) dp[i][1] = 0;
                    break;
                }
                if (a[j].l <= a[i].l && a[i].l <= a[j].r && !flag1) {
                    dp[i][0] = min(dp[j][0]+abs(a[j].l-a[i].l), dp[j][1]+abs(a[j].r-a[i].l));
                    flag1 = 1;
                }
                if (a[j].r >= a[i].r && a[i].r >= a[j].l && !flag2) {    
                    dp[i][1] =  min(dp[j][1]+abs(a[j].r-a[i].r), dp[j][0]+abs(a[j].l-a[i].r));
                    flag2 = 1;
                }
            }
        }
        int ans = min(dp[n+1][0], dp[n+1][1]) + y;
        cout<<ans<<endl;
    }

    return 0;
}