给你一个整数数组 arr 和一个整数值 target 。
请你在 arr 中找 两个互不重叠的子数组 且它们的和都等于 target 。可能会有多种方案,请你返回满足要求的两个子数组长度和的 最小值 。
请返回满足要求的最小长度和,如果无法找到这样的两个子数组,请返回 -1 。
一个map用来保存从0-index i 的前缀和以及索引 ------mp[前缀和] = 索引
一个dp用来保存不大于目前索引i的最小长度的子数组长度, 如果不存在, 则为maxn
用一个sum做累加, 同时对map进行更新
可知当mp中含有sum - target时可以找到一个子数组
设置cur = 找到的新子数组长度
bfindex = 此数组之前的(与之不重叠的) 序号
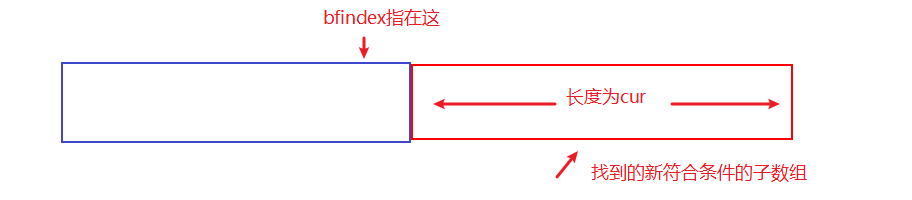
则可以由是否存在dp[bfindex]判断此前是否已经有符合条件的数组
如果有:
[ans = min (ans, cur + dp[bfindex])
]
不管有没有 :
[dp[i] = min(dp[i-1], cur)
]
注意当i==0的特殊情况, 不然会造成数组访问越界, 这里我用了个if判断
ac代码 :
int minSumOfLengths(vector<int>& arr, int target) {
const int maxn = 0x3f3f3f3f;
int n = arr.size();
int sum = 0;
int ans = maxn;
vector<int> dp(n, maxn);
map<int, int> mp;
mp[0] = -1;
for (int i = 0; i < n; ++i)
{
sum += arr[i];
if(i)
dp[i] = dp[i - 1];
if (mp.count(sum - target)) {
int cur = i - mp[sum - target];
int bfindex = mp[sum - target];
if (bfindex >= 0 && dp[bfindex] < maxn) {
ans = min(ans, cur + dp[bfindex]);
}
if(i)
dp[i] = min(dp[i-1], cur);
else
dp[i] = min(cur, maxn);
}
mp[sum] = i;
}
return ans == maxn ? -1 : ans;
}