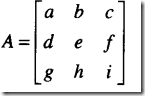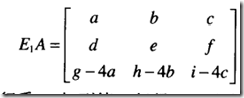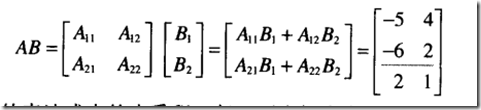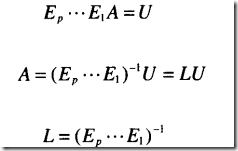矩阵运算
矩阵加法，标量乘法，矩阵乘法。
A(BC)=(AB)C 矩阵乘法顺序无关
AB=AC 不能推出 B = C 因为A可能不是列向量线性无关。
矩阵的逆
这里讨论的是n*n的方阵，若矩阵可逆逆矩阵是唯一的，存在逆矩阵的矩阵又称为非奇异矩阵。
怎样判断一个矩阵是否存在逆矩阵呢，即是否该矩阵是 非奇异矩阵呢？
对于2*2的矩阵
即detA != 0 则该矩阵是 非奇异矩阵， 注意对于 2*2 如果 detA=0 即ad=bc 则 c/a = d/b 假设 a!=0 b!=0 这意味这 A的列向量是线性相关的！ –> 是否线性相关等价与是否非奇异 ？
如果是线性相关的A必然不是满秩不能映射生成R^n,而存在可逆矩阵，意味着可以生成[1 0 … 0] [0 1 … 0] … [0 0 … 1] 这就意味着可以生成R^n是矛盾的。
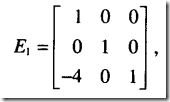
初等矩阵
单位矩阵进行一次行变换得到就是初等矩阵。
左乘对应行变换，右乘对应列变换。
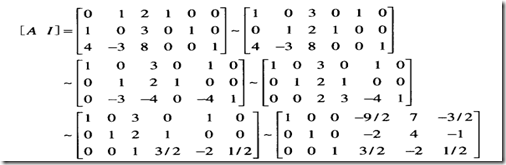
n*n的矩阵A是可逆的，当且仅当A行等价与I_n,把A变为I_n的一些列初等变换同时把I_n变成A^-
这对于逆矩阵的一种求解方法
这个思路和前面第一章那个矩阵映射中关于单位向量的观点是一致的。 这其实就是解方程转换成阶梯矩阵的过程，只不过进一步向上使得主元上面都是0。
可逆矩阵的特征
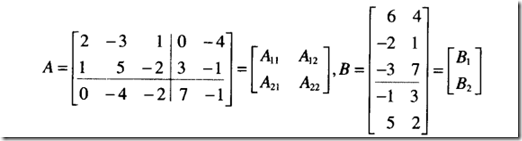
分块矩阵
分块矩阵的乘法
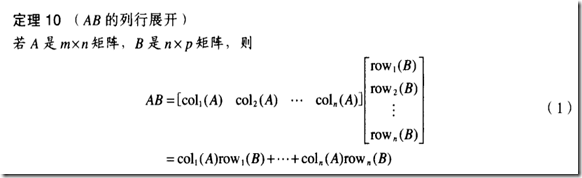
矩阵的乘法AB=C 可以将C的列向量看做是B中的一列向量对于A中的列向量的操纵线性相加。
也可以将C的行看做A中的一行向量对于B中行向量的操作线性相加。
可以看出 AB=C <=> B^TA^T=C^T 也说明了上面的性质。 A^T的列操纵B^T的列也即A的行操纵B的行。(横看成岭侧成峰）
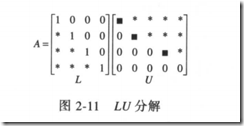
矩阵分解(LU分解）
LU分解 适用于解一系列具有相同系数矩阵的线性方程。
Ax=b L(Ux)=b Ly=b
即解
Ly=b
Ux=y
分解算法
为什么用LU分解解方程而不用 A^- b 求解？
