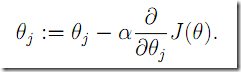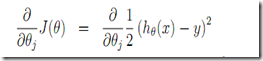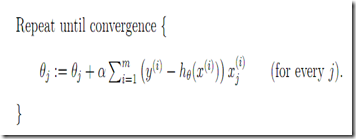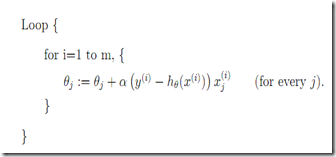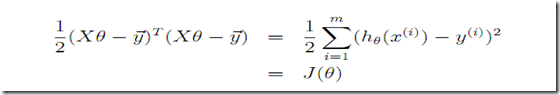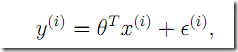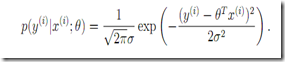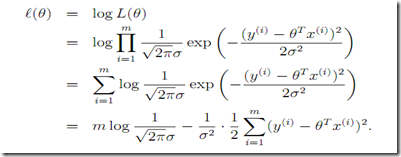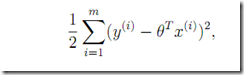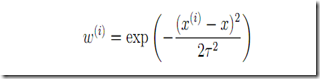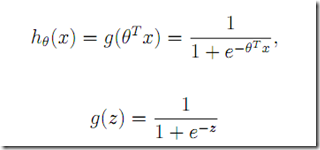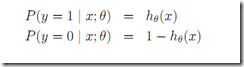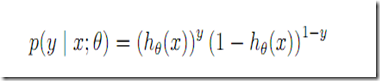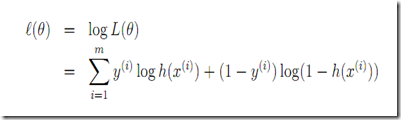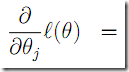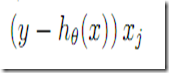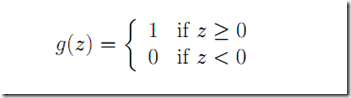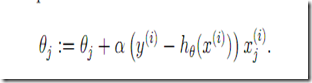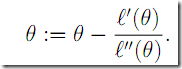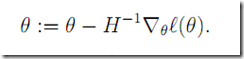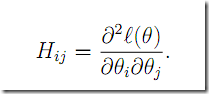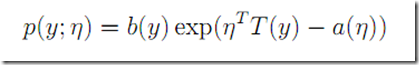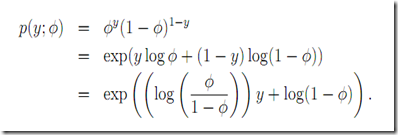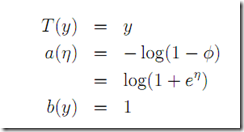1. 线性拟合问题的迭代解法
- batch gradient descent
梯度下降法，每次沿着梯度方向对于参数移动小的距离。
有两种具体实现，一种是每次移动的时候考虑所有的实验点，这种在训练集合较大的时候开销比较大。(如下，每次扫描所有m个试验点)
另外一种是stochastic gradient deseent
扫描每个点的时候就决定了参数的按照该点的梯度进行参数调整。即
每次参数调整只考虑当前一个试验点。这个收敛速度会更快，但是不保证能收敛到最佳，但是如果逐步调小
的值可以收敛到最佳。
我个人觉得gradient descent的方法都是依赖起始位置吧，最终都是一个局部最优结果。
2. 矩阵的导数(matrix derivative)，矩阵的迹（trace)
3. 最小二乘法
这里课件利用矩阵的导数定义(这里 是一个向量其实)，矩阵的trace的特性
结果于从向量投影角度理解最小二乘解法是一致的。
4. 概率角度看
5. 局部加权线性回归
就是说当我们考虑预测Y=f(X)的时候，要优先考虑X附近的试验点的特性，他们给予较高的权重，而距离X较远的试验点影响系数要小一些。
前面讲到的优化算法的目标步骤如下
而对于locally weighted linear regression
这样离X近的点影响因子会大
局部加权应该效果会更好一些，但是普通的线性回归我们离线计算好参数就OK了，在线不需要载入训练的点数据了。
但是局部加权则需要在计算每一个Y=f(x)的时候都要载入训练数据,对于不同的X,不同。
局部加权线性回归是一种non-parametric的方法。
6. 分类与逻辑回归
假设分类目标就是{0,1}两种可能。预测分类
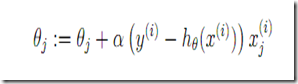梯度法规则 注意和线性回归是形式是一样的 但是不是一个线性函数了（g(z))。
7. perceptron学习方法
与上面的logsitic g(z)输出0-1之间的值不同，这里让g(z)只输出0或者1
8. 牛顿法
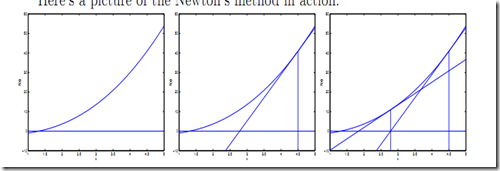
上图展示了利用牛顿法求解f(x) = 0
那么对应到我们的最小二乘问题
=0
Newton-Raphson 针对是向量的情况
H - Hessian
9. 推广的线性模型
指数系
都可以写为下面的形式
考虑上面的逻辑回归对应的伯努利模型
注意
对照参考下《语音与语言处理》P231
预测 如果我们用线性模型去拟合
显然不合适因为右侧取值可以是任意值而左侧是[0,1]
那么我们可以考虑利用去预测odds
但是左侧还是属于, 于是我们最左侧取 log OK 这个时候就和上面一致了。。。