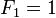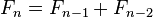算法——动态规划算法

动态规划法基本思想：将原问题分解为相似的子问题，在求解的过程中通过子问题的解求出原问题的解。
著名的应用实例有：求解最短路径问题，背包问题，项目管理，网络流优化等。

个人对动态规划的理解，主要就是避免重复计算。就是那些曾经发生过的事情，曾经计算过的值先保存下来，然后再次遇到相同的子问题的时候，直接用保存好的值给出，不再进行计算。

有一个很简单的例子，关于斐波那契数列。

什么是斐波那契数列？根据维基百科的解释是这样的，

费波那西数列（Fibonacci Sequence），又译费波拿契数、斐波那契数列、费氏数列、黄金分割数列。

在数学上，费波那西数列是以递归的方法来定义：

• • 
  • 
  • 

用文字来说，就是费波那西数列由 0 和 1 开始，之后的费波那西系数就由之前的两数相加。

写出C语言的话，简单就是这样的：

int fib(int n)
{
    if(n==0||n==1)
        return 1;
    return fib(n-1)+fib(n-2);
}

当你求fib(5)的时候，简单到最后就是好多个fib(1)和fib (0)而已。

当n=5时，fib(5)的计算过程如下:

1. 1. fib(5)
   2. fib(4) + fib(3)
   3. (fib(3) + fib(2)) + (fib(2) + fib(1))
   4. ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
   5. (((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))

所以很多计算过程都是重复的，这样对于计算机来说太浪费了，所以希望避免重复的过程再次发生，好比我们写函数一样，就是为了更加有效率。

利用动态规划的思想，先将计算过的值保存下来，之后如果发现有相同步骤的时候，直接将事先保存好的值拿出来就好。

 

所以鄙人是这样写的：

//动态规划法
int m[10];
bool bn[10];
int fib2(int n)
{
    if(!bn[n])//检查是否已经计算过
    {
        m[n]=fib2(n-1)+fib2(n-2);//保存已经计算过的值
        bn[n]=true;
    }
    return m[n];
}


int _tmain(int argc, _TCHAR* argv[])
{
    //初始化数据
    for(int i=0;i<5;i++)
        bn[i]=false;
    m[1]=m[0]=1;
    bn[0]=bn[1]=true;

    printf("%d",fib2(5));
    return 0;
}

相比算法导论给的实例，维基百科给的更加容易理解。（越来越发现自己离不开网络了）