LeetCode5：最长回文子串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2：

输入: "cbbd"
输出: "bb"

这题有4种解法，暴力解法，中心扩散法，动态规划，manacher算法。暴力算法不做解释，manacher太高深，先不学了。

中心扩散法

从边界情况，即子串长度为1或者2的情况向两边扩散，如果两边相同就可以加长回串的长度，最后返回最长的子串。

class Solution {
public:
    pair<int, int> expandAroundCenter(const string& s, int left, int right) {
        while (left >= 0 && right < s.size() && s[left] == s[right]) {
            --left;
            ++right;
        }
        return {left + 1, right - 1};
    }

    string longestPalindrome(string s) {
        int start = 0, end = 0;
        for (int i = 0; i < s.size(); ++i) {
            auto [left1, right1] = expandAroundCenter(s, i, i);
            auto [left2, right2] = expandAroundCenter(s, i, i + 1);
            if (right1 - left1 > end - start) {
                start = left1;
                end = right1;
            }
            if (right2 - left2 > end - start) {
                start = left2;
                end = right2;
            }
        }
        return s.substr(start, end - start + 1);
    }
};

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/longest-palindromic-substring/solution/zui-chang-hui-wen-zi-chuan-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

长度为1的中心子串有n个，长度为2的中心子串有n-1个，每个中心子串扩展都是O(n)次，时间复杂度为O(n^2)，空间复杂度为O(1)。

动态规划

动态规划在于找到状态转移方程。如果一个子串是回文串，而且该串的两侧的两个字符是相同的，那么加上两次的字符的新串也是回文串。

转移方程可以写成如下形式：

 而对于边界条件，要么中心子串是一个字符，要么是两个相同的字符。

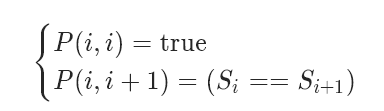
class Solution {
public:
    string longestPalindrome(string s)
    {
        if(s.size()==0) return s;
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n));
        int maxlen = 0, maxi = 0, maxj = 0;
        
        dp[0][0]=1;

        for (int j = 1; j < n; j++)
        {   
            dp[j][j]=1;
            dp[j-1][j]=(s[j-1]==s[j])?2:0;
            if(dp[j-1][j]>maxlen){
                maxlen = dp[j-1][j];
                maxi = j-1;
                maxj = j;
            }
            for (int i = 0; i < j-1; i++)
            {
                if ((s[i] == s[j]) && ((dp[i + 1][j - 1] != 0) || (j - i < 3)))
                {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                    if (dp[i][j] > maxlen)
                    {
                        maxlen = dp[i][j];
                        maxi = i;
                        maxj = j;
                    }
                }
                else
                    dp[i][j] = 0;
            }
        }
        return s.substr(maxi, maxj-maxi+1 );
    }
};

这里采用给一个上三角的n*n的二位数组记录这个位置横纵坐标(i,j)对应的子串（即从i到j）是否为回文串，如果不是则为0，如果是则代表该回文子串的长度。

因为(i,j)是否为回文取决于(i+1,j-1)，所以需要先计算出每一个位置左下方的值，才能得出当前位置的值。边界条件即为[i][i]位置全为1，[i-1][i]位置的值取决于这两个位置的字符是否相同。

循环按照按列循环的顺序进行，一共进行n-1次列循环，对于每列进行n-2次行循环，时间复杂度为O(n^2)，空间复杂度为O(n^2)。