数据结构
数据结构有什么作用?
当我们使用者java官网给我吗提供的容器的时候,ArraiList其实就是无限扩容的数组
LinkedList其实是一个链表.
现实世界中存储数据,我们要通过一些工具或者建模来进行存储,每种数据结构都有自己的优缺点
而算法,在这么多的数据中如何以最快的速度实现插入.删除.查找数据问题
我们java语言是一种面向对象的编程语言,java和c相比就是自动挡 Python是无人机 高度封装
数据结构就是变速箱,不懂数据结构原理的,对于开发java程序也没有问题.
如果你懂变速箱的原理,那么不但可以开车还可以修车
常见数据结构: 堆栈,队列,数组,链表,红黑树,
栈
-
堆栈:stack,又称堆栈,他是运算受限的线性表结构,他的限制是仅允许在标的的一端进行插入和删除操作,不允许在其他任何位置进行添加查找删除等操作.
简单的说,采用该结构的集合,对元素的存取有以下特点:
-
先进后出(存进去的元素,要在他后面的元素依次取出后,才能取出该元素).例如:子弹要压进弹夹和子弹夹弹出的动作.
-
栈的入口.出口在同一个位置 即栈顶
-
空栈 : 栈顶和栈底重合,栈内没有任何元素
-
栈底:栈的最低层元素 栈内最先入栈的元素的位置
-
栈顶: 栈的出入口,栈的最顶层元素的头部位置
-
压栈: 就是存储元素,把元素存储到栈的顶端位置,栈中已有的元素依次向栈底方向移动一个位置.
-
弹栈:就是取出元素,把栈的顶端位置元素取出,栈中已有的元素依次向栈顶方向移动一个位置.

-
-
队列
-
队列: queue, 简称堆,它同堆栈几乎一样的,也是一种运算受限的线性表结构,它的限制是仅允许在标的的一端进行插入,在标的的另一端进行删除.
简单的说,采用该结构的集合,对元素的存取有以下特点:
-
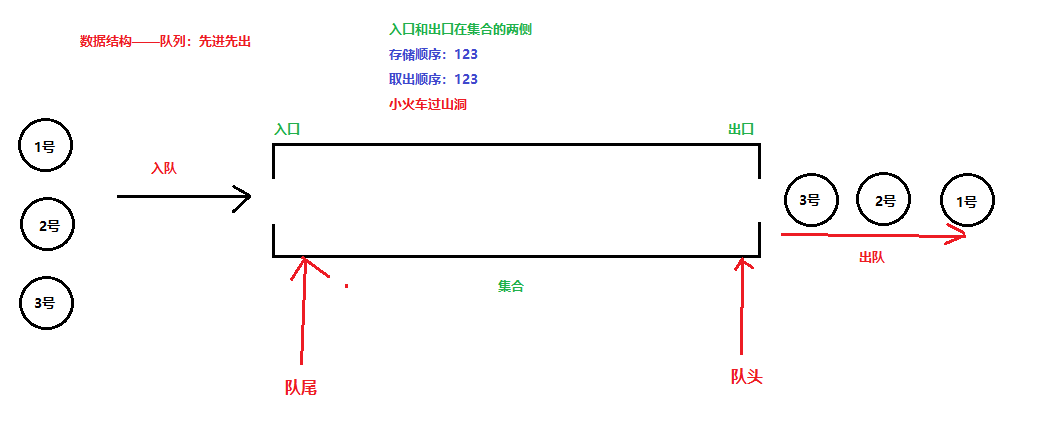
先进先出(存进去的元素,要在他前面的元素依次取出后,才能取出该元素)例如:火车过山洞,火车头先进山洞,火车头先从山洞出来,车位后进来最后出来.
-
队列的入口/出口各占一侧
-
入队:在入口一侧添加元素, 队尾
-
出队:在入口另一侧删除元素 队头
-
-
数组
-
数组 :Array,是有序的元素序列,数组在内存当中开辟一段连续的空间,并在此空间内存储元素. 例如:
生活中的酒店酒店当中的房间是连续的,不间断,有50个房间,房间号从001-050每个房间都有固定的编号,通过编号就可以快速找到酒店房间的住户.
简单的说,采用此结构的集合,对元素存取有以下特点:
-
查找元素块:通过索引,可以快速的访问到指定位置的元素.
-
增删元素慢:
-
指定索引位置增删元素,需要创建一个新数组,将指定的新元素储存到指定的索引位置,再把源数组元素根据他原来的索引,复制到新数组对应的索引位置.
-
指定索引位置删除元素:需要创建一个新数组,把源数组当中的元素根据索引,复制到新数组对应索引的位置,源数组中指定的索引位置元素复制到新数组当中.
原理图如下:
-

链表结构
-
链表:linked list,由一系列节点node(链表当中的每个元素称为节点)组成,节点可以在运行时动态生成.每个节点上包含两个部分:一个是用于存储数据元素的数据域,另一个是用来存储下一个节点地址的指针域.我们常说链表结构有单向链表和双向链表
-
单向链表:链表当中只有一条链子,不能保证元素的顺序(存储元素的顺序和抽取出的元素顺序,有可能不一致)
-
双向链表:链表当中有两条链子,有一条链子是专门记录元素的顺序,是有序的集合.()
链表结构特点:链表存入数据是打乱了之后存储,但是双向链表会多出一条用来记录进入链表元素的顺序,所以使用了双链表的集合,会拥有索引.比单链条多出的指向域多出一个,这个指向域存储着自己的地址,并没有什么用,只是方便给与上一个节点得到本身的地址.
查询慢:链表结果的地址不是连接,每次查询元素,都必须从头开始查询
曾删快: 在链表结果中,增加或删除一个元素,对链表的整体结果没有影响
-
多个节点之间,通过地址进行连接的,比如:多个人玩丢手绢,每个人右手拉住下一个人的左手,上一个人的左手拉住该人的右手,依次类推,多个人就被连接起来,
-
查找元素比较慢:想要查找某个元素,需要通过链接的节点依次向后查找指定的元素
-
删除元素比较快:
1.增加一个元素:只需要修改连接下个元素的地址即可.
2.删除一个元素:只需要修改连接下一个元素的地址即可.
红黑树:
-
二叉树binary tree,每个节点数不超过2的有序树(tree)
简单的理解,就是类似于我们生活中的数的结构,只不过每个节点上都最多只能有两个子节点
顶上的节点成为根节点,两边的被称为左子树和右子树
在二叉树的结构中,有一种比较特殊的红黑树,红黑树本身就是一个二叉树
红黑树的约束:
1.节点可以是红色的也可以是黑色的
2.根节点是黑色的
3.树叶节点(空节点)是黑色的
4.每个红色节点的子节点都是黑色的
5.任何一个节点到其每一个叶子节点的所有路径上的黑色节点数是相同的,
红黑树的特点:
查询速度非常快,趋*于*衡树,查找叶子元素最小和最大次数不能超过两倍.
