Properties in Algebra

附录-Properties in Algebra

部分证明转载自标注，仅作个人整理查阅用。

范数 (norm) (^{[1]})

要更好的理解范数，就要从函数、几何与矩阵的角度去理解，我尽量讲的通俗一些。我们都知道，函数与几何图形往往是有对应的关系，这个很好想象，特别是在三维以下的空间内，函数是几何图像的数学概括，而几何图像是函数的高度形象化，比如一个函数对应几何空间上若干点组成的图形。但当函数与几何超出三维空间时，就难以获得较好的想象，于是就有了映射的概念，映射表达的就是一个集合通过某种关系转为另外一个集合。通常数学书是先说映射，然后再讨论函数，这是因为函数是映射的一个特例。
为了更好的在数学上表达这种映射关系，（这里特指线性关系）于是就引进了矩阵。这里的矩阵就是表征上述空间映射的线性关系。而通过向量来表示上述映射中所说的这个集合，而我们通常所说的基，就是这个集合的最一般关系。于是，我们可以这样理解，一个集合（向量），通过一种映射关系（矩阵），得到另外一个集合（另外一个向量）。
那么向量的范数，就是表示这个原有集合的大小；而矩阵的范数，就是表示这个变化过程的大小的一个度量。那么说到具体几几范数，其不过是定义不同，一个矩阵范数往往由一个向量范数引出，我们称之为算子范数，其物理意义都如我上述所述。

具体怎么用，看不同的领域，看你来自计算机领域 用的比较多的就是迭代过程中收敛性质的判断，如果理解上述的意义，在计算机领域，一般迭代前后步骤的差值的范数表示其大小，常用的是二范数，差值越小表示越逼近实际值，可以认为达到要求的精度，收敛。

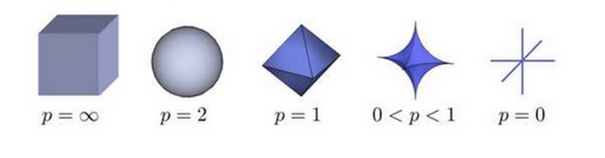
L-p范数定义

[L_p=Vert xVert_p=sqrt[p]{sum_{i=1}^{n}x_i^p}，x=(x_1,dots,x_n) ]

上图表示了p从无穷到0变化时，三维空间中到原点的距离（范数）为1的点构成的图形的变化情况。以常见的L-2范数（p=2）为例，此时的范数也即欧氏距离，空间中到原点的欧氏距离为1的点构成了一个球面。

(L_0)范数

[L_0=Vert xVert_0=sqrt[0]{sum_{i=1}^{n}x_i^0}::=#{i|x_i eq0} ]

在实际应用中，由于(L_0)范数本身不容易有一个好的数学表示形式，给出上面问题的形式化表示是一个很难的问题，故被人认为是一个NP难问题。所以在实际情况中，(L_0)的最优问题会被放宽到(L_1)或(L_2)下的最优化。 在通常情况下，大家都用"0范数"表示向量(x)中非零元素的个数。

(L_1)范数

表示向量(x)中非零元素的绝对值之和。

[L_1=Vert xVert_1=sqrt[1]{sum_{i=1}^{n}x_i^1}::=sum_{i=1}^{n}|x_i| ]

(L_1)范数有很多的名字，例如我们熟悉的曼哈顿距离、最小绝对误差等。使用(L_1)范数可以度量两个向量间的差异，如绝对误差和（Sum of Absolute Difference）.

(L_2)范数

我们用的最多的度量距离：欧氏距离就是一种(L_2)范数，它的定义如下：

[L_2=Vert xVert_2=sqrt[2]{sum_{i=1}^{n}x_i^2} ]

(L_infty)范数

主要用来表示向量元素中的最大项值，通常用此来表示：

[L_infty=Vert xVert_infty=::=max{|x_i|} ]

实对称矩阵

对称矩阵（Symmetric Matrices）：是指以主对角线为对称轴，各元素对应相等的矩阵。在线性代数中，对称矩阵是一个方形矩阵，其转置矩阵和自身相等。

[A=A^T ]

实对称矩阵：如果有n阶矩阵A，其矩阵的元素都为实数，且矩阵A的转置等于其本身（(a_{ij}=a_{ji})），则称A为实对称矩阵。

实对称矩阵里的元素全是实数，而对称矩阵只说明(A=A^T)，没说明矩阵中的元素是实数， 阵中的元素不仅可以是实数，也可以是虚数，甚至元素本身就是一个矩阵或其它更一般的数学对象，实对称矩阵就说明了矩阵中的元素要是实数。

• 性质1：实对称矩阵的特征值都是实数

[ ]

• 性质2：实对称属于不同特征值的特征向量正交

[ ]

• 性质3：若(lambda_0)是实对称矩阵A的 k 重特征值，则与对(lambda_0)应的有 k 个线性无关的特征向量

[ ]

• 性质4：n 阶实对称矩阵 正交相似 于以特征值为对角的对角矩阵。

[ ]

矩阵的逆

若方阵(A)满足(|A| eq0)，则称(A)为非退化方阵或非奇异方阵，反正，则称其为退化方阵，下令(A=(a_{ij}))为一非退化方阵，令：

[B'=frac{(A_{ij})}{|A|} ]

则有(AB=BA=I)，称(B)为(A)的逆，记作(B=A^{-1})，易证(B)也是一个非退化方阵，且(A)的逆是唯一的。

• (AA^{-1}=A^{-1}A=I)
• ((A')^{-1}=(A^{-1})')
• 若(A,C)均为(p)阶非退化方阵，则：((AC)^{-1}=C^{-1}A^{-1})
• (|A|^{-1}=|A^{-1}|)
• 若(A)为正交矩阵，则(A^{-1}=A')
• 若(A=diag(a_{ii}))非退化，则：(A^{-1}=diag(a_{ii}^{-1}))
• 若(A,B)为非退化方阵，则

[left( egin{array}{cc} A&O\ O&B end{array} ight)^{-1}= left( egin{array}{cc} A^{-1}&O\ O&B^{-1} end{array} ight) ]

非奇异矩阵的分块矩阵求逆

设(A)是(p)阶满秩矩阵，它的逆矩阵为(A^{-1}),他们可表示为下列分块矩阵：

[A=left( egin{array}{c|c} A_{11}&A_{12}\hline A_{21}&A_{22} end{array} ight)， A^{-1}=left( egin{array}{c|c} A^{11}&A^{12}\hline A^{21}&A^{22} end{array} ight) ]

其中(A_{11},A^{11})均为(r imes r)矩阵，(A_{22},A^{22})均为(s imes s)矩阵，且(r+s=p)。

(^{[1]})范数对于数学的意义？1范数、2范数、无穷范数