codeforce 896D

一道比较良心的数论题：

枚举VIP的个数 x，求出第一种人个数的范围 [L,R]。 
用类似求卡特兰数的方法可以得出答案为 

C(n，x)=∑（i=L to R）C(n−x，i)−C(n−x，i+1)。

证明如下：我们可以先取X个VIP客人出来，因为其可以插入任意的位置。

那么我们只要求合法的50,100元客户序列。

我们先看一下卡特兰数的推导：

------------------------------------------------------分割线--------------------------------------------------------------------------

 事实上，可以认为问题是，任意两种操作，要求每种操作的总次数一样，且进行第k次操作2前必须先进行至少k次操作1。我们假设一个人在原点，操作1是此人沿右上角45°走一个单位（一个单位设为根号2，这样他第一次进行操作1就刚好走到（1,1）点），操作2是此人沿右下角45°走一个单位。第k次操作2前必须先进行至少k次操作1，就是说明所走出来的折线不能跨越x轴走到y=-1这条线上！在进行n次操作1和n此操作2后，此人必将到到达（2n，0）！若无跨越x轴的限制，折线的种数将为C（2n，n），即在2n次操作中选出n次作为操作1的方法数。

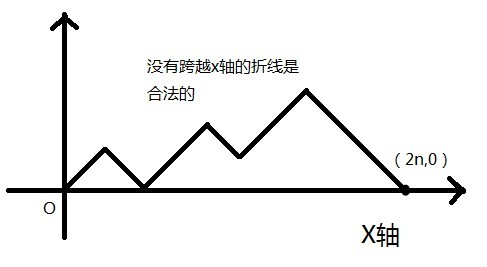
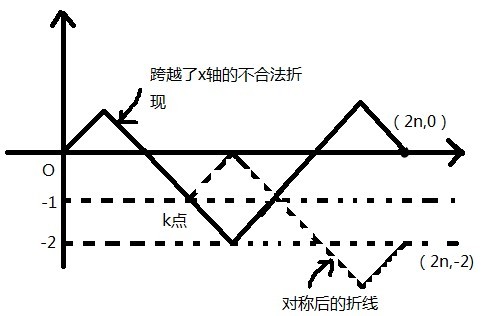
现在只要减去跨越了x轴的情况数。对于任意跨越x轴的情况，必有将与y=-1相交。找出第一个与y=-1相交的点k，将k点以右的折线根据y=-1对称（即操作1与操作2互换了）。可以发现终点最终都会从（2n，0）对称到（2n，-2）。由于对称总是能进行的，且是可逆的。我们可以得出所有跨越了x轴的折线总数是与从（0,0）到（2n,-2）的折线总数。而后者的操作2比操作1要多0-（-2）=2次。即操作1为n-1,操作2为n+1。总数为C（2n，n-1）。

 

------------------------------------------------------分割线----------------------------------------------------------------------

我们同样推导，50元视为向上走，100元视为向下走，那么我们设50元X，100元Y，那么我们的目标点为（X+Y,X-Y），有C（2X,X-Y）种走法。

我们作对称点（X+Y，-2-X+Y）,有C（2Y-2，X-Y-2）种方法，我们将其化简，可以得到C（X+Y，X）-C（X+Y，X+1）。

那么公式便简化成:

    ans=∑C(N,i)*(C(N-i,L)-C(N-i,R+1)),我们考虑如和处理模数。

我们在统计阶乘时，把与模数的GCD提出来，最后计算时乘（除）回去。

就酱紫。

#include<bits/stdc++.h>
#define sight(c) ('0'<=c&&c<='9')
#define LL long long
#define int LL 
#define N 100017
#define dg  
inline void read(int &x){
    static char c;
    for (c=getchar();!sight(c);c=getchar());
    for (x=0;sight(c);c=getchar())x=x*10+c-48;
}
using namespace std;
void write(int x){if (x<10) {putchar('0'+x); return;} write(x/10); putchar('0'+x%10);}
inline void writel(int x){ if (x<0) putchar('-'),x*=-1; write(x); putchar('
'); }
LL qsm(LL x,LL y,LL mo) {
    static LL anw;
    for (anw=1;y;y>>=1,x=x*x%mo)  if (y&1) anw=anw*x%mo; 
    return anw;
}
int a[N>>10],tot,p,l,r,n,x,c[N][N>>10];
LL t,mo,f[N],ni[N],AA1,AA2,AA3,ANW,ans;
void Int() {
    t=mo=p; 
    for (int i=2;i*i<=p;i++)  {
        if (p%i==0) a[++tot]=i;
        while (p%i==0) p/=i;
    }  if (p^1) a[++tot]=p;
    for (int i=1;i<=tot;i++) t=t/a[i]*(a[i]-1);
    f[0]=ni[0]=1;
    for (int i=1;i<=n+7;i++) {
        x=i; for (int j=1;j<=tot;j++) {
         c[i][j]=c[i-1][j];
         while (x%a[j]==0) c[i][j]++,x/=a[j];}
        f[i]=f[i-1]*x%mo; 
        ni[i]=qsm(f[i],t-1,mo);
    } 
}
LL C(int x,int y) {
    if (x<y) return 0;
    if (!y) return 1;
    static LL anw; anw=f[x]*ni[y]%mo*ni[x-y]%mo;
    for (int i=1;i<=tot;i++) anw=anw*qsm(a[i],c[x][i]-c[y][i]-c[x-y][i],mo)%mo;
    return anw; 
}
LL ask(int siz){
    AA1=C(n,siz); 
    AA2=C(siz,siz+l+1>>1);
    AA3=C(siz,(min(siz,r)+siz>>1)+1);
    ANW=(AA2-AA3)%mo; if (ANW<0) ANW+=mo;
//    dg("%d %d %d
",AA2,AA3,AA1);
    return ANW*AA1%mo;
}
signed main () {
//    freopen("d.in","r",stdin);
    read(n); read(p); read(l); read(r);
    Int();
    for (int i=n;~i;i--) 
      (ans+=ask(n-i))%=mo;
    writel(ans%mo>=0?ans%mo:ans%mo+mo);
    return 0;
}