28 | 堆和堆排序:为什么说堆排序没有快速排序快? https://time.geekbang.org/column/article/69913
https://baike.baidu.com/item/堆/20606834
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。
完全二叉树
数据存储
数组下标 与 二叉树节点
数据下标i, 父节点i//2 左子节点2i 右节点2i+1
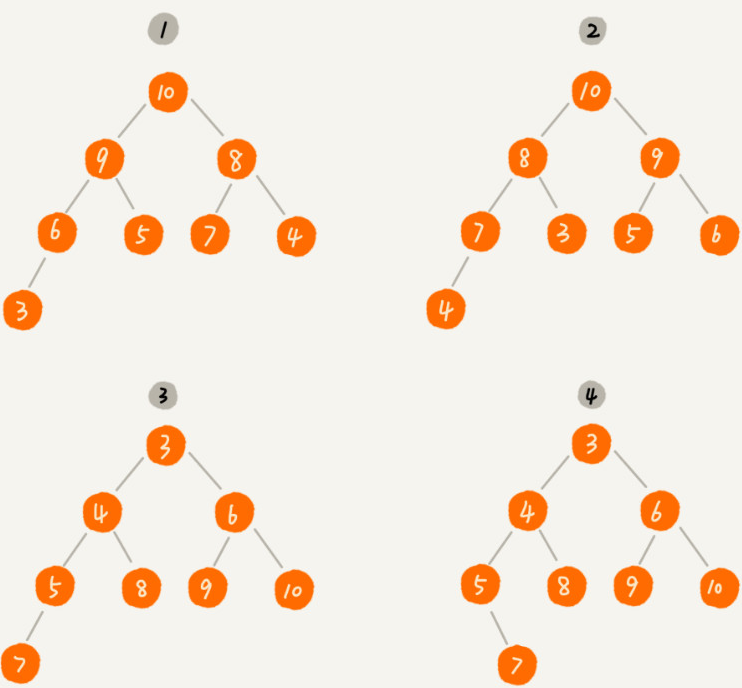
前面我们提到,堆是一种特殊的树。我们现在就来看看,什么样的树才是堆。我罗列了两点要求,只要满足这两点,它就是一个堆。堆是一个完全二叉树;堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。我分别解释一下这两点。第一点,堆必须是一个完全二叉树。还记得我们之前讲的完全二叉树的定义吗?完全二叉树要求,除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列。第二点,堆中的每个节点的值必须大于等于(或者小于等于)其子树中每个节点的值。实际上,我们还可以换一种说法,堆中每个节点的值都大于等于(或者小于等于)其左右子节点的值。这两种表述是等价的。对于每个节点的值都大于等于子树中每个节点值的堆,我们叫做“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆,我们叫做“小顶堆”。
大根堆 小根堆
其中第 1 个和第 2 个是大顶堆,第 3 个是小顶堆,第 4 个不是堆。除此之外,从图中还可以看出来,对于同一组数据,我们可以构建多种不同形态的堆。
完全二叉树
数据存储
数组下标 与 二叉树节点
数据下标i, 父节点i//2 左子节点2i 右节点2i+1
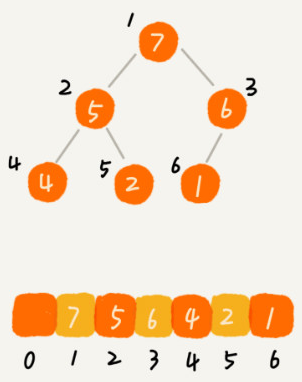
要实现一个堆,我们先要知道,堆都支持哪些操作以及如何存储一个堆。我之前讲过,完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针,单纯地通过数组的下标,就可以找到一个节点的左右子节点和父节点。
我画了一个用数组存储堆的例子,你可以先看下。从图中我们可以看到,数组中下标为 i 的节点的左子节点,就是下标为 i∗2 的节点,右子节点就是下标为 i∗2+1 的节点,父节点就是下标为 2i 的节点。知道了如何存储一个堆,那我们再来看看,堆上的操作有哪些呢?我罗列了几个非常核心的操作,分别是往堆中插入一个元素和删除堆顶元素。(如果没有特殊说明,我下面都是拿大顶堆来讲解)。