https://zh.wikipedia.org/wiki/欧拉定理_(数论)
费马小定理的推广
http://www.sec.ntnu.edu.tw/Monthly/95(286-295)/293-pdf/04.pdf
在数论中,欧拉定理(也称费马-欧拉定理或欧拉 φ {displaystyle {varphi }}  函数定理)是一个关于同余的性质。欧拉定理表明,若 n , a {displaystyle n,a}
函数定理)是一个关于同余的性质。欧拉定理表明,若 n , a {displaystyle n,a}  为正整数,且 n , a {displaystyle n,a}
为正整数,且 n , a {displaystyle n,a}  互素(即 gcd ( a , n ) = 1 {displaystyle gcd(a,n)=1}
互素(即 gcd ( a , n ) = 1 {displaystyle gcd(a,n)=1}  ),则
),则
a φ ( n ) ≡ 1 ( mod n ) {displaystyle a^{varphi (n)}equiv 1{pmod {n}}} 
即 a φ ( n ) {displaystyle a^{varphi (n)}}  与1在模n下同余;φ(n)为欧拉函数。欧拉定理得名于瑞士数学家莱昂哈德·欧拉。
与1在模n下同余;φ(n)为欧拉函数。欧拉定理得名于瑞士数学家莱昂哈德·欧拉。
欧拉定理实际上是费马小定理的推广。
证明
一般的证明中会用到“所有与 n {displaystyle n}  互質的同余类构成一个群”的性质,也就是说,设 { a 1 ¯ , a 2 ¯ , ⋯ , a φ ( n ) ¯ } {displaystyle left{{overline {a_{1}}},{overline {a_{2}}},cdots ,{overline {a_{varphi (n)}}}
ight}}
互質的同余类构成一个群”的性质,也就是说,设 { a 1 ¯ , a 2 ¯ , ⋯ , a φ ( n ) ¯ } {displaystyle left{{overline {a_{1}}},{overline {a_{2}}},cdots ,{overline {a_{varphi (n)}}}
ight}}  是比 n {displaystyle n}
是比 n {displaystyle n}  小的正整数中所有与 n {displaystyle n}
小的正整数中所有与 n {displaystyle n}  互素的数对应的同余类组成的集合(这个集合也称为模n 的简化剩余系)。这些同余类构成一个群,称为整数模n乘法群。因为此群阶为 φ ( n ) {displaystyle varphi (n)}
互素的数对应的同余类组成的集合(这个集合也称为模n 的简化剩余系)。这些同余类构成一个群,称为整数模n乘法群。因为此群阶为 φ ( n ) {displaystyle varphi (n)}  ,所以 a φ ( n ) ≡ 1 ( mod n ) {displaystyle a^{varphi (n)}equiv 1{pmod {n}}}
,所以 a φ ( n ) ≡ 1 ( mod n ) {displaystyle a^{varphi (n)}equiv 1{pmod {n}}}  。
。
当 n {displaystyle n}  是素数的时候, φ ( n ) = n − 1 {displaystyle varphi (n)=n-1}
是素数的时候, φ ( n ) = n − 1 {displaystyle varphi (n)=n-1}  ,所以欧拉定理变为:
,所以欧拉定理变为:
- a n − 1 ≡ 1 ( mod n ) {displaystyle a^{n-1}equiv 1{pmod {n}}}
 或
或 - a n ≡ a ( mod n ) {displaystyle a^{n}equiv a{pmod {n}}}

这就是费马小定理。
https://en.wikipedia.org/wiki/Euler's_theorem
In number theory, Euler's theorem (also known as the Fermat–Euler theorem or Euler's totient theorem) states that if n and a are coprime positive integers, then
- a φ ( n ) ≡ 1 ( mod n ) {displaystyle a^{varphi (n)}equiv 1{pmod {n}}}

where φ ( n ) {displaystyle varphi (n)}  is Euler's totient function. (The notation is explained in the article Modular arithmetic.) In 1736, Leonhard Euler published his proof of Fermat's little theorem,[1] which Fermat had presented without proof. Subsequently, Euler presented other proofs of the theorem, culminating with "Euler's theorem" in his paper of 1763, in which he attempted to find the smallest exponent for which Fermat's little theorem was always true.[2]
is Euler's totient function. (The notation is explained in the article Modular arithmetic.) In 1736, Leonhard Euler published his proof of Fermat's little theorem,[1] which Fermat had presented without proof. Subsequently, Euler presented other proofs of the theorem, culminating with "Euler's theorem" in his paper of 1763, in which he attempted to find the smallest exponent for which Fermat's little theorem was always true.[2]
The converse of Euler's theorem is also true: if the above congruence is true, then a {displaystyle a}  and n {displaystyle n}
and n {displaystyle n}  must be coprime.
must be coprime.
The theorem is a generalization of Fermat's little theorem, and is further generalized by Carmichael's theorem.
The theorem may be used to easily reduce large powers modulo n {displaystyle n}  . For example, consider finding the ones place decimal digit of 7 222 {displaystyle 7^{222}}
. For example, consider finding the ones place decimal digit of 7 222 {displaystyle 7^{222}}  , i.e. 7 222 ( mod 10 ) {displaystyle 7^{222}{pmod {10}}}
, i.e. 7 222 ( mod 10 ) {displaystyle 7^{222}{pmod {10}}}  . The integers 7 and 10 are coprime, and φ ( 10 ) = 4 {displaystyle varphi (10)=4}
. The integers 7 and 10 are coprime, and φ ( 10 ) = 4 {displaystyle varphi (10)=4}  . So Euler's theorem yields 7 4 ≡ 1 ( mod 10 ) {displaystyle 7^{4}equiv 1{pmod {10}}}
. So Euler's theorem yields 7 4 ≡ 1 ( mod 10 ) {displaystyle 7^{4}equiv 1{pmod {10}}}  , and we get 7 222 ≡ 7 4 × 55 + 2 ≡ ( 7 4 ) 55 × 7 2 ≡ 1 55 × 7 2 ≡ 49 ≡ 9 ( mod 10 ) {displaystyle 7^{222}equiv 7^{4 imes 55+2}equiv (7^{4})^{55} imes 7^{2}equiv 1^{55} imes 7^{2}equiv 49equiv 9{pmod {10}}}
, and we get 7 222 ≡ 7 4 × 55 + 2 ≡ ( 7 4 ) 55 × 7 2 ≡ 1 55 × 7 2 ≡ 49 ≡ 9 ( mod 10 ) {displaystyle 7^{222}equiv 7^{4 imes 55+2}equiv (7^{4})^{55} imes 7^{2}equiv 1^{55} imes 7^{2}equiv 49equiv 9{pmod {10}}}  .
.
In general, when reducing a power of a {displaystyle a}  modulo n {displaystyle n}
modulo n {displaystyle n}  (where a {displaystyle a}
(where a {displaystyle a}  and n {displaystyle n}
and n {displaystyle n}  are coprime), one needs to work modulo φ ( n ) {displaystyle varphi (n)}
are coprime), one needs to work modulo φ ( n ) {displaystyle varphi (n)}  in the exponent of a {displaystyle a}
in the exponent of a {displaystyle a}  :
:
- if x ≡ y ( mod φ ( n ) ) {displaystyle xequiv y{pmod {varphi (n)}}}
 , then a x ≡ a y ( mod n ) {displaystyle a^{x}equiv a^{y}{pmod {n}}}
, then a x ≡ a y ( mod n ) {displaystyle a^{x}equiv a^{y}{pmod {n}}}  .
.
Euler's theorem is sometimes cited as forming the basis of the RSA encryption system, however it is insufficient (and unnecessary) to use Euler's theorem to certify the validity of RSA encryption. In RSA, the net result of first encrypting a plaintext message, then later decrypting it, amounts to exponentiating a large input number by k φ ( n ) + 1 {displaystyle kvarphi (n)+1}  , for some positive integer k {displaystyle k}
, for some positive integer k {displaystyle k}  . In the case that the original number is relatively prime to n {displaystyle n}
. In the case that the original number is relatively prime to n {displaystyle n}  , Euler's theorem then guarantees that the decrypted output number is equal to the original input number, giving back the plaintext. However, because n {displaystyle n}
, Euler's theorem then guarantees that the decrypted output number is equal to the original input number, giving back the plaintext. However, because n {displaystyle n}  is a product of two distinct primes, p {displaystyle p}
is a product of two distinct primes, p {displaystyle p}  and q {displaystyle q}
and q {displaystyle q}  , when the number encrypted is a multiple of p {displaystyle p}
, when the number encrypted is a multiple of p {displaystyle p}  or q {displaystyle q}
or q {displaystyle q}  , Euler's theorem does not apply and it is necessary to use the uniqueness provision of the Chinese Remainder Theorem. The Chinese Remainder Theorem also suffices in the case where the number is relatively prime to n {displaystyle n}
, Euler's theorem does not apply and it is necessary to use the uniqueness provision of the Chinese Remainder Theorem. The Chinese Remainder Theorem also suffices in the case where the number is relatively prime to n {displaystyle n}  , and so Euler's theorem is neither sufficient nor necessary.
, and so Euler's theorem is neither sufficient nor necessary.
Proofs
1. Euler's theorem can be proven using concepts from the theory of groups:[3] The residue classes modulo n that are coprime to n form a group under multiplication (see the article Multiplicative group of integers modulo n for details). The order of that group is φ(n) where φ denotes Euler's totient function. Lagrange's theorem states that the order of any subgroup of a finite group divides the order of the entire group, in this case φ(n). If a is any number coprime to n then a is in one of these residue classes. Thus, group element a has finite order k, and its powers a, a2, ... , ak modulo n form a subgroup of the group of residue classes, with ak ≡ 1 (mod n). Lagrange's theorem says k must divide φ(n), i.e. there is an integer M such that kM = φ(n). This then implies,
- a φ ( n ) = a k M = ( a k ) M ≡ 1 M = 1 ≡ 1 ( mod n ) . {displaystyle a^{varphi (n)}=a^{kM}=(a^{k})^{M}equiv 1^{M}=1equiv 1{pmod {n}}.}

2. There is also a direct proof:[4][5] Let R = {x1, x2, ... , xφ(n)} be a reduced residue system (mod n) and let a be any integer coprime to n. The proof hinges on the fundamental fact that multiplication by a permutes the xi: in other words if axj ≡ axk (mod n) then j = k. (This law of cancellation is proved in the article Multiplicative group of integers modulo n.[6]) That is, the sets R and aR = {ax1, ax2, ... , axφ(n)}, considered as sets of congruence classes (mod n), are identical (as sets—they may be listed in different orders), so the product of all the numbers in R is congruent (mod n) to the product of all the numbers in aR:
- ∏ i = 1 φ ( n ) x i ≡ ∏ i = 1 φ ( n ) a x i = a φ ( n ) ∏ i = 1 φ ( n ) x i ( mod n ) , {displaystyle prod _{i=1}^{varphi (n)}x_{i}equiv prod _{i=1}^{varphi (n)}ax_{i}=a^{varphi (n)}prod _{i=1}^{varphi (n)}x_{i}{pmod {n}},}

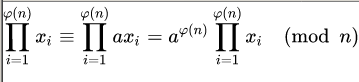 and using the cancellation law to cancel each xi gives Euler's theorem:
and using the cancellation law to cancel each xi gives Euler's theorem:
- a φ ( n ) ≡ 1 ( mod n ) . {displaystyle a^{varphi (n)}equiv 1{pmod {n}}.}

Euler quotient
The Euler quotient of an integer a with respect to n is defined as:
- q n ( a ) = a φ ( n ) − 1 n {displaystyle q_{n}(a)={frac {a^{varphi (n)}-1}{n}}}

The special case of an Euler quotient when n is prime is called a Fermat quotient.
Any odd number n that divides q n ( 2 ) {displaystyle q_{n}(2)}  is called a Wieferich number. This is equivalent to saying that 2φ(n) ≡ 1 (mod n2). As a generalization, any number n that is coprime to a positive integer a, and such that n divides q n ( a ) {displaystyle q_{n}(a)}
is called a Wieferich number. This is equivalent to saying that 2φ(n) ≡ 1 (mod n2). As a generalization, any number n that is coprime to a positive integer a, and such that n divides q n ( a ) {displaystyle q_{n}(a)}  , is called a (generalized) Wieferich number to base a. This is equivalent to saying that aφ(n) ≡ 1 (mod n2).
, is called a (generalized) Wieferich number to base a. This is equivalent to saying that aφ(n) ≡ 1 (mod n2).














或















, then
.









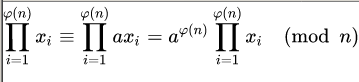 and using the cancellation law to cancel each xi gives Euler's theorem:
and using the cancellation law to cancel each xi gives Euler's theorem:





