https://rdipietro.github.io/friendly-intro-to-cross-entropy-loss/
【将输入转化为输出:概率分布】
When we develop a model for probabilistic classification, we aim to map the model's inputs to probabilistic predictions, and we often train our model by incrementally adjusting the model's parameters so that our predictions get closer and closer to ground-truth probabilities.
In this post, we'll focus on models that assume that classes are mutually exclusive. For example, if we're interested in determining whether an image is best described as a landscape or as a house or as something else, then our model might accept an image as input and produce three numbers as output, each representing the probability of a single class.
During training, we might put in an image of a landscape, and we hope that our model produces predictions that are close to the ground-truth class probabilities y=(1.0,0.0,0.0)Ty=(1.0,0.0,0.0)T. If our model predicts a different distribution, say y^=(0.4,0.1,0.5)Ty^=(0.4,0.1,0.5)T, then we'd like to nudge the parameters so that y^y^ gets closer to yy.
【cross entropy 交叉熵 提供了一种量化的解决办法】
But what exactly do we mean by "gets closer to"? In particular, how should we measure the difference between y^y^ and yy?
This post describes one possible measure, cross entropy, and describes why it's reasonable for the task of classification.
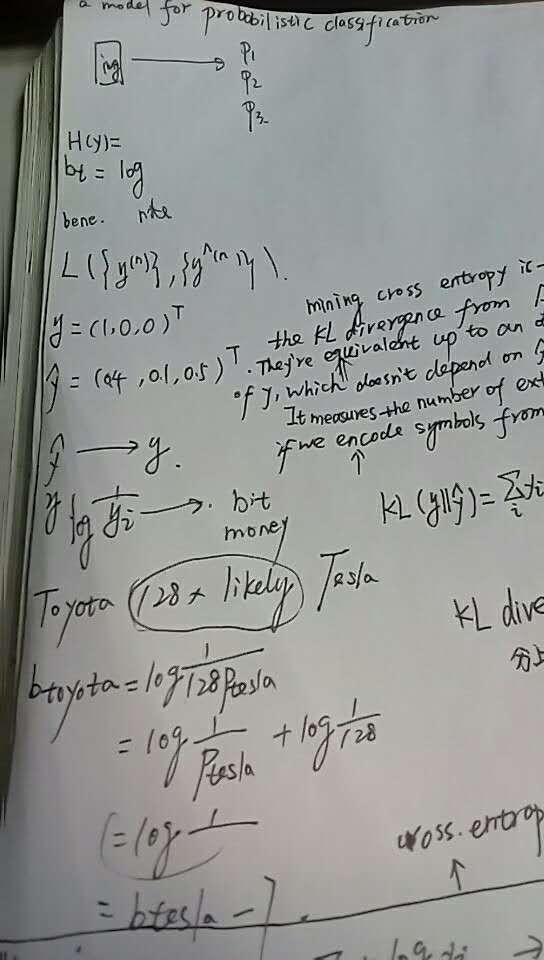
https://rdipietro.github.io/friendly-intro-to-cross-entropy-loss/

zh.wikipedia.org/wiki/相对熵
KL散度是两个概率分布P和Q差别的非对称性的度量。 KL散度是用来 度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下,P表示数据的真实分布,Q表示数据的理论分布,模型分布,或P的近似分布。
en.wikipedia.org/wiki/Kullback–Leibler_divergence
In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q. By analogy with information theory, it is also called the relative entropy of P with respect to Q. In the context of coding theory, DKL(P‖Q) can be constructed as measuring the expected number of extra bits required to codesamples from P using a code optimized for Q rather than the code optimized for P.
https://rdipietro.github.io/friendly-intro-to-cross-entropy-loss/
When we develop a probabilistic model over mutually exclusive classes, we need a way to measure the difference between predicted probabilities y^y^ and ground-truth probabilities yy, and during training we try to tune parameters so that this difference is minimized.