How to avoid Over-fitting using Regularization?

http://www.mit.edu/~9.520/scribe-notes/cl7.pdf

https://en.wikipedia.org/wiki/Bayesian_interpretation_of_kernel_regularization

the degree to which instability and complexity of the estimator should be penalized (higher penalty for increasing value of {displaystyle lambda })

https://www.analyticsvidhya.com/blog/2015/02/avoid-over-fitting-regularization/ 

Regularization can be motivated as a technique to improve the generalizability of a learned model.

 https://en.wikipedia.org/wiki/Regularization_(mathematics)

Regularization can be motivated as a technique to improve the generalizability of a learned model.

The goal of this learning problem is to find a function that fits or predicts the outcome (label) that minimizes the expected error over all possible inputs and labels. The expected error of a function  is:

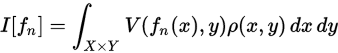
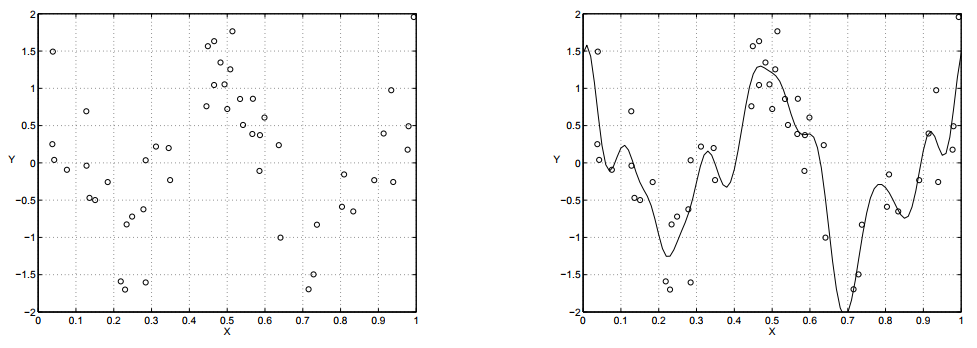
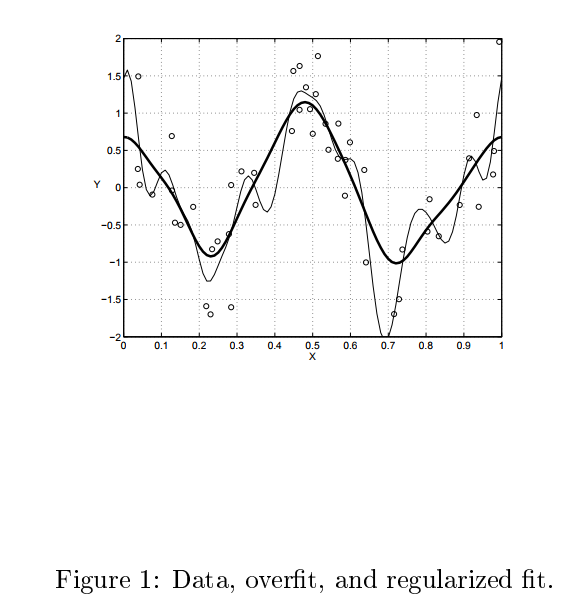
Typically in learning problems, only a subset of input data and labels are available, measured with some noise. Therefore, the expected error is unmeasurable, and the best surrogate available is the empirical error over the  available samples:

Without bounds on the complexity of the function space (formally, the reproducing kernel Hilbert space) available, a model will be learned that incurs zero loss on the surrogate empirical error. If measurements (e.g. of ) were made with noise, this model may suffer from overfitting and display poor expected error. Regularization introduces a penalty for exploring certain regions of the function space used to build the model, which can improve generalization.