https://www.cs.toronto.edu/~hinton/absps/JMLRdropout.pdf
Deep neural nets with a large number of parameters are very powerful machine learning
systems. However, overfitting is a serious problem in such networks. Large networks are also
slow to use, making it difficult to deal with overfitting by combining the predictions of many
different large neural nets at test time. Dropout is a technique for addressing this problem.
The key idea is to randomly drop units (along with their connections) from the neural
network during training. This prevents units from co-adapting too much. During training,
dropout samples from an exponential number of different “thinned” networks. At test time,
it is easy to approximate the effect of averaging the predictions of all these thinned networks
by simply using a single unthinned network that has smaller weights. This significantly
reduces overfitting and gives major improvements over other regularization methods. We
show that dropout improves the performance of neural networks on supervised learning
tasks in vision, speech recognition, document classification and computational biology,
obtaining state-of-the-art results on many benchmark data sets.
Deep neural networks contain multiple non-linear hidden layers and this makes them very
expressive models that can learn very complicated relationships between their inputs and
outputs. With limited training data, however, many of these complicated relationships
will be the result of sampling noise, so they will exist in the training set but not in real
test data even if it is drawn from the same distribution. This leads to overfitting and many
methods have been developed for reducing it. These include stopping the training as soon as
performance on a validation set starts to get worse, introducing weight penalties of various
kinds such as L1 and L2 regularization and soft weight sharing (Nowlan and Hinton, 1992).
With unlimited computation, the best way to “regularize” a fixed-sized model is to
average the predictions of all possible settings of the parameters, weighting each setting by
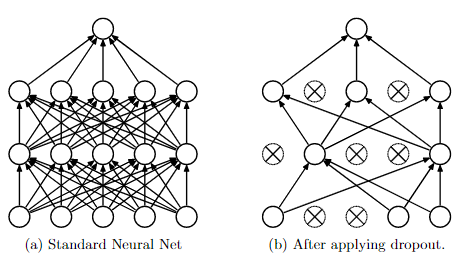
Figure 1:
Dropout Neural Net Model.
Left
: A standard neural net with 2 hidden layers.
Right
:
An example of a thinned net produced by applying dropout to the network on the left.
Crossed units have been dropped.
its posterior probability given the training data. This can sometimes be approximated quite
well for simple or small models (Xiong et al., 2011; Salakhutdinov and Mnih, 2008), but we
would like to approach the performance of the Bayesian gold standard using considerably
less computation. We propose to do this by approximating an equally weighted geometric
mean of the predictions of an exponential number of learned models that share parameters.
Model combination nearly always improves the performance of machine learning meth-
ods. With large neural networks, however, the obvious idea of averaging the outputs of
many separately trained nets is prohibitively expensive. Combining several models is most
helpful when the individual models are different from each other and in order to make
neural net models different, they should either have different architectures or be trained
on different data. Training many different architectures is hard because finding optimal
hyperparameters for each architecture is a daunting task and training each large network
requires a lot of computation. Moreover, large networks normally require large amounts of
training data and there may not be enough data available to train different networks on
different subsets of the data. Even if one was able to train many different large networks,
using them all at test time is infeasible in applications where it is important to respond
quickly.
Dropout is a technique that addresses both these issues. It prevents overfitting and
provides a way of approximately combining exponentially many different neural network
architectures efficiently. The term “dropout” refers to dropping out units (hidden and
visible) in a neural network. By dropping a unit out, we mean temporarily removing it from
the network, along with all its incoming and outgoing connections, as shown in Figure 1.
The choice of which units to drop is random. In the simplest case, each unit is retained with
a fixed probability p independent of other units, where p can be chosen using a validation
set or can simply be set at 0.5, which seems to be close to optimal for a wide range of
networks and tasks. For the input units, however, the optimal probability of retention is
usually closer to 1 than to 0.5.
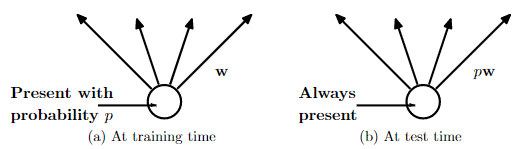
Figure 2:
Left
: A unit at training time that is present with probability
p
and is connected to units
in the next layer with weights
w
.
Right
: At test time, the unit is always present and
the weights are multiplied by
p
. The output at test time is same as the expected output
at training time.
Applying dropout to a neural network amounts to sampling a “thinned” network from
it. The thinned network consists of all the units that survived dropout (Figure 1b). A
neural net with
n
units, can be seen as a collection of 2
n
possible thinned neural networks.
These networks all share weights so that the total number of parameters is still
O
(
n
2
), or
less. For each presentation of each training case, a new thinned network is sampled and
trained. So training a neural network with dropout can be seen as training a collection of 2
n
thinned networks with extensive weight sharing, where each thinned network gets trained
very rarely, if at all.
At test time, it is not feasible to explicitly average the predictions from exponentially
many thinned models. However, a very simple approximate averaging method works well in
practice. The idea is to use a single neural net at test time without dropout. The weights
of this network are scaled-down versions of the trained weights. If a unit is retained with
probability
p
during training, the outgoing weights of that unit are multiplied by
p
at test
time as shown in Figure 2. This ensures that for any hidden unit the
expected
output (under
the distribution used to drop units at training time) is the same as the actual output at
test time. By doing this scaling, 2
n
networks with shared weights can be combined into
a single neural network to be used at test time. We found that training a network with
dropout and using this approximate averaging method at test time leads to significantly
lower generalization error on a wide variety of classification problems compared to training
with other regularization methods.
The idea of dropout is not limited to feed-forward neural nets. It can be more generally
applied to graphical models such as Boltzmann Machines. In this paper, we introduce
the dropout Restricted Boltzmann Machine model and compare it to standard Restricted
Boltzmann Machines (RBM). Our experiments show that dropout RBMs are better than
standard RBMs in certain respects..