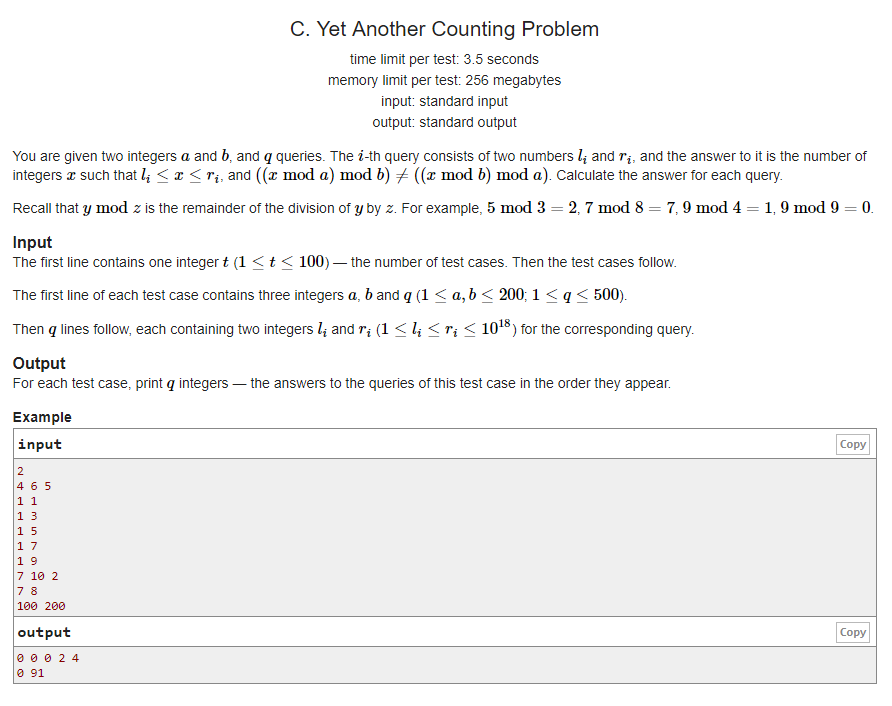
我们对其中一组样例进行打表,可以发现a*b(找lcm(a,b)好像也行)是一段循环节,其中满足条件的数的个数相同
那么,面对这样的区间问题,我们可以用(l-1)/(ab)计算出l之前有多少个循环节,(l-1)%(ab)计算出(l-1)(ab)与l之间的差值,在[1,ab]之间的满足条件的数的个数可以用前缀和预处理后进行o(1)的查询,之后便是查询前缀和s[(l-1)%(ab)]即可,这样就求出了l之前满足条件的数的个数
然后在同理求得r之前(包括r)这样的数的个数,相减即答案。这样的操作既优化了时间,又避免了区间之间的分类讨论。
long long a, b, q;
long long s[maxn];
long long cal(long long x)
{
return x / (a * b) * s[a * b] + s[x % (a * b)];
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t;
cin >> t;
while (t--)
{
cin >> a >> b >> q;
for (int i = 1; i <= a * b; i++)
s[i] = s[i - 1] + (i % a % b != i % b % a);
while (q--)
{
long long x, y;
cin >> x >> y;
cout << cal(y) - cal(x - 1) << " ";
}
cout << endl;
}
return 0;
}