（计算几何板子）四边形与圆的重叠面积

https://nanti.jisuanke.com/t/43493

计算几何是什么阴间东西就不用我多说了8，写作计算几何读作大模拟

首先介绍本题需要的板子:

double pi = acos(-1);//π
const double eps = 1e-9;//ε误差区间

inline int dcmp(double x)//cmp x with 0
{
    if (fabs(x) <= eps)return 0;
    return x < 0 ? -1 : 1;
}
inline int cmp(double x, double y)//比较浮点数
{
    //x>y return 1
    //x<y reutrn -1
    //x==y return 0
    return dcmp(x - y);
}

double max(double x, double y)//手写浮点max
{
    return dcmp(x - y) > 0 ? x : y;
}
double min(double x, double y)
{
    return dcmp(x - y) < 0 ? x : y;//手写浮点min
}

定义在欧几里得平面的point

struct Point {
    double x, y;
    Point() {}
    Point(double xx, double yy) { x = xx; y = yy; }
    Point operator -(Point s) { return Point(x - s.x, y - s.y); }//重载运算符
    Point operator +(Point s) { return Point(x + s.x, y + s.y); }
    double operator *(Point s) { return x * s.x + y * s.y; }
    double operator ^(Point s) { return x * s.y - y * s.x; }
}p[6];

double len(Point a) { return sqrt(a * a); }//vector(o,a)的长度
double dis(Point a, Point b) { return len(b - a); }//两点之间的距离

叉乘(满足右手定则，有正负),a为公共点,vector(a,b)叉乘vector(a,c)

double cross(Point a, Point b, Point c)
{
    return (b - a) ^ (c - a);
}

点乘，即vector(a,b)的模乘上vector(a,c)在vector(a,b)方向上的投影（有方向），得到一个有正负的值

double dot(Point a, Point b, Point c)//点乘 ,a为公共点
{
    return (b - a) * (c - a);
}

然后就是本题的解法：

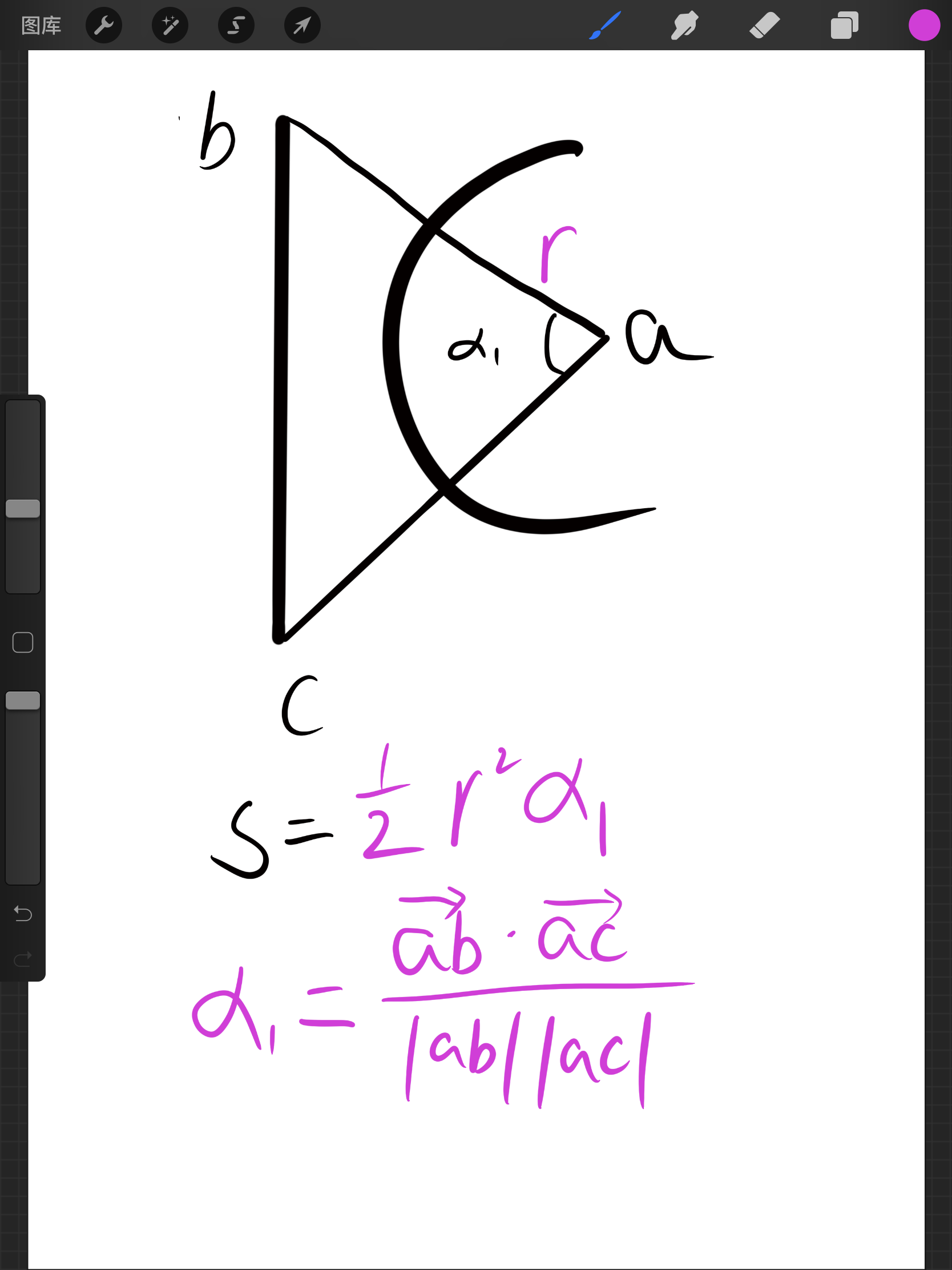
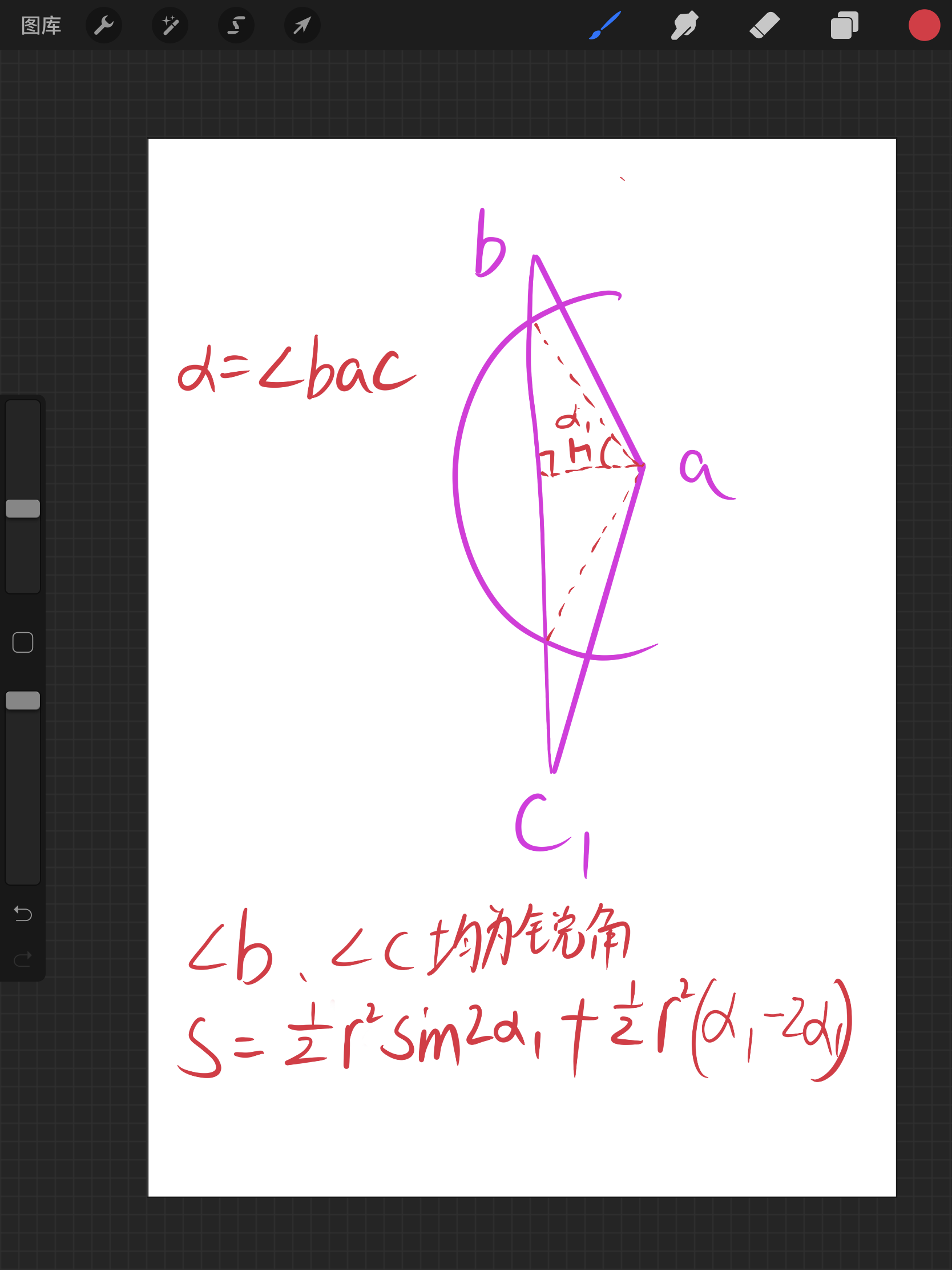
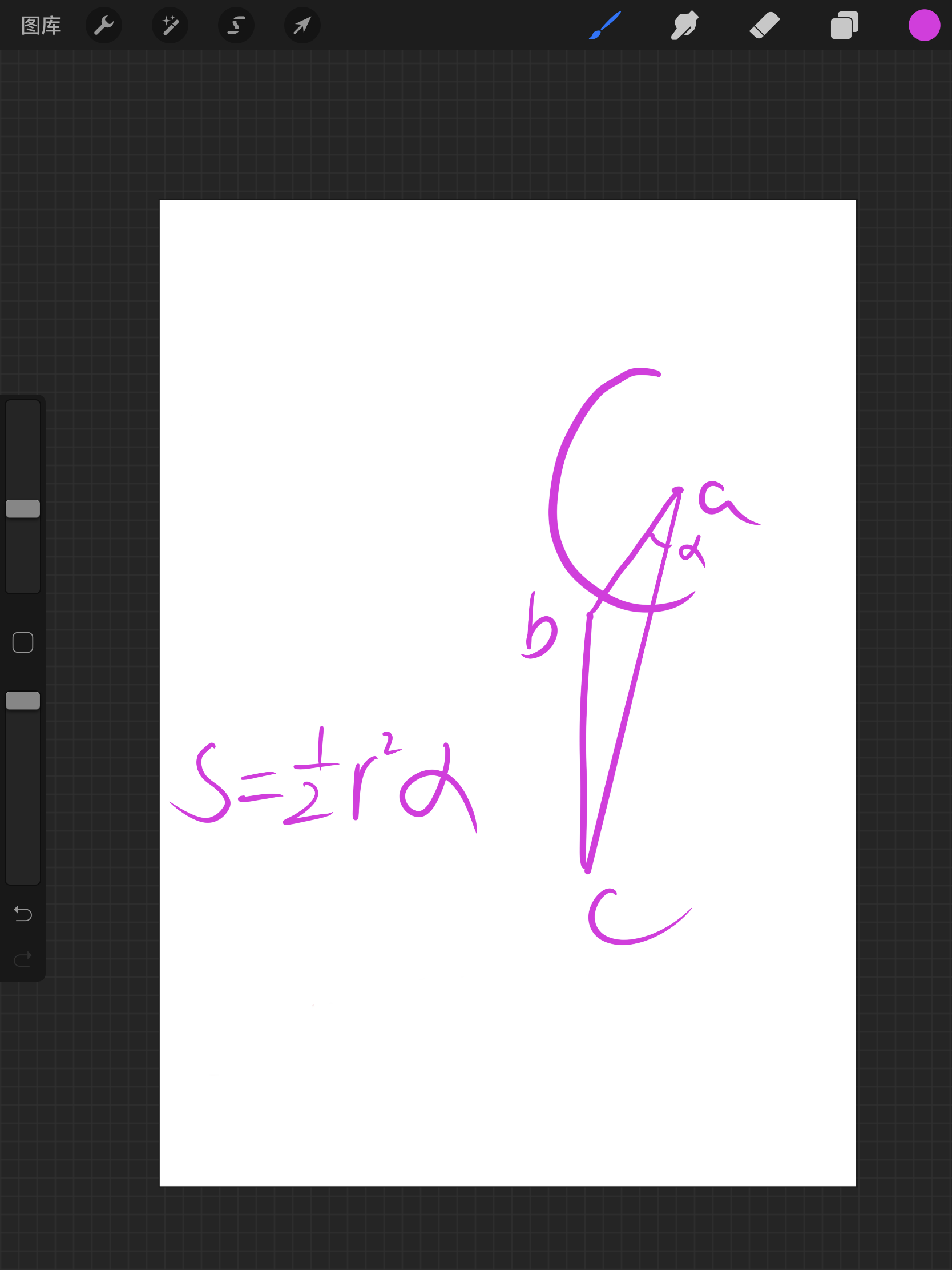
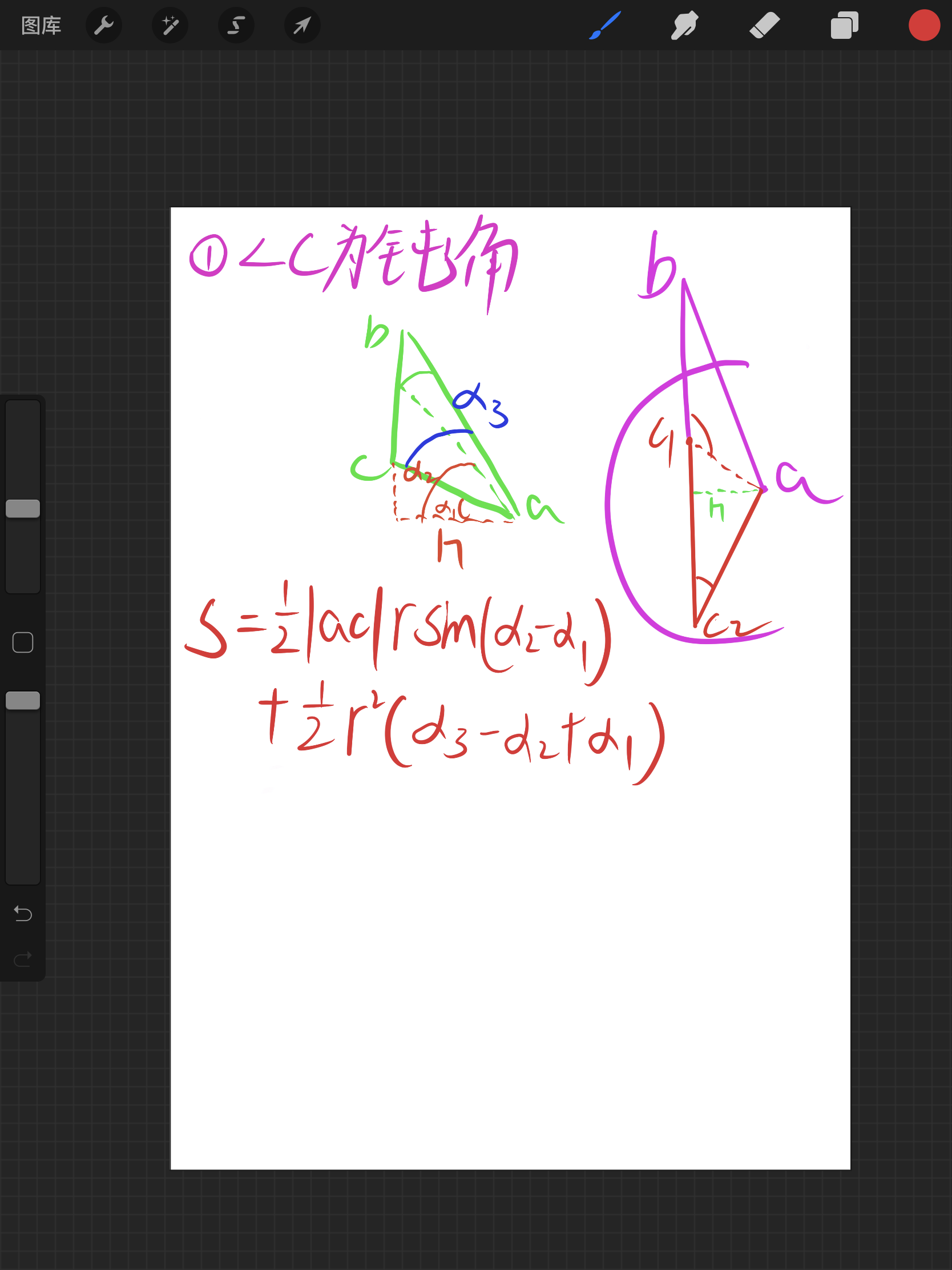
由于计算的是面积，只需要最后判断叉乘方向然后加到ans上去就行了

下面是代码

#pragma GCC optimize(2)
#include<bits/stdc++.h>
#define ll long long
#define fastio {ios::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);};
using namespace std;
const ll inf = 1e17 + 7;
const int maxn = 3e5 + 10;

double pi = acos(-1);
const double eps = 1e-9;

inline int dcmp(double x)//cmp x with 0
{
    if (fabs(x) <= eps)return 0;
    return x < 0 ? -1 : 1;
}
inline int cmp(double x, double y)
{
    //x>y return 1
    //x<y reutrn -1
    //x==y return 0
    return dcmp(x - y);
}

double max(double x, double y)
{
    return dcmp(x - y) > 0 ? x : y;
}
double min(double x, double y)
{
    return dcmp(x - y) < 0 ? x : y;
}

struct Point {
    double x, y;
    Point() {}
    Point(double xx, double yy) { x = xx; y = yy; }
    Point operator -(Point s) { return Point(x - s.x, y - s.y); }
    Point operator +(Point s) { return Point(x + s.x, y + s.y); }
    double operator *(Point s) { return x * s.x + y * s.y; }
    double operator ^(Point s) { return x * s.y - y * s.x; }
}p[6];

double len(Point a) { return sqrt(a * a); }
double dis(Point a, Point b) { return len(b - a); }//两点之间的距离

double cross(Point a, Point b, Point c)//叉乘,a为公共点
{
    return (b - a) ^ (c - a);
}
double dot(Point a, Point b, Point c)//点乘 ,a为公共点
{
    return (b - a) * (c - a);
}
int judge(Point a, Point b, Point c)//判断c是否在ab线段上（前提是c在直线ab上）
{
    if (c.x >= min(a.x, b.x)
        && c.x <= max(a.x, b.x)
        && c.y >= min(a.y, b.y)
        && c.y <= max(a.y, b.y)) return 1;
    return 0;
}
double area(Point b, Point c, double r)
{
    Point a(0.0, 0.0);
    if (dis(b, c) < eps)return 0.0;
    double h = fabs(cross(a, b, c) / dis(b, c));
    if (dis(b, a) - r > eps&& dis(c, a) - r > eps)//two point out of the circle
    {
        double angle = acos(dot(a, b, c) / dis(b, a) / dis(c, a));
        if (h - r > eps)return 0.5 * r * r * angle;
        if (dot(b, a, c) > 0 && dot(c, a, b) > 0)
        {
            double angle1 = 2 * acos(h / r);
            return 0.5 * r * r * fabs(angle - angle1) + 0.5 * r * r * sin(angle1);
        }
        return 0.5 * r * r * angle;
    }
    else if (dis(b, a) - r < eps && dis(c, a) - r < eps)return 0.5 * fabs(cross(a, b, c));//two point in the circle
    else {
        if (dis(c, a) > dis(b, a))swap(b, c);
        if (fabs(dis(a, c)) < eps)return 0.0;
        if (dot(c, a, b) < 0)
        {
            double angle1 = acos(h / dis(c, a)), angle2 = acos(h / r), angle3 = acos(dot(a, b, c) / dis(b, a) / dis(c, a));
            return 0.5 * dis(c, a) * r * sin(angle2 - angle1) + 0.5 * r * r * (angle3 - angle2 + angle1);
        }
        else
        {
            double angle1 = acos(h / r), angle2 = acos(h / dis(c, a)), angle3 = acos(dot(a, b, c) / dis(b, a) / dis(c, a));
            return 0.5 * r * dis(c, a) * sin(angle1 + angle2) + 0.5 * r * r * (angle3 - angle2 - angle1);
        }
    }
}


int main()
{
    double x, y, r;
    double Ax, Ay, Bx, By;
    scanf("%lf%lf%lf%lf%lf%lf%lf", &x, &y, &r, &Ax, &Ay, &Bx, &By);
    p[1] = { Ax,Ay };
    p[2] = { Ax,By };
    p[3] = { Bx,By };
    p[4] = { Bx,Ay };
    p[5] = p[1];
    Point O(x, y);
    for (int i = 1; i <= 5; i++)
        p[i] = p[i] - O;
    O = Point(0.0, 0.0);//让O为原点
    double sum = 0;
    for(int i=1;i<=4;i++)
    {
        int j = i + 1;
        double s = area(p[i], p[j], r);
        if (cross(O, p[i], p[j]) > 0)sum += s;//通过叉乘正负判断面积的方向
        else sum -= s;
    }
    printf("%.4lf", fabs(sum));
    return 0;
}