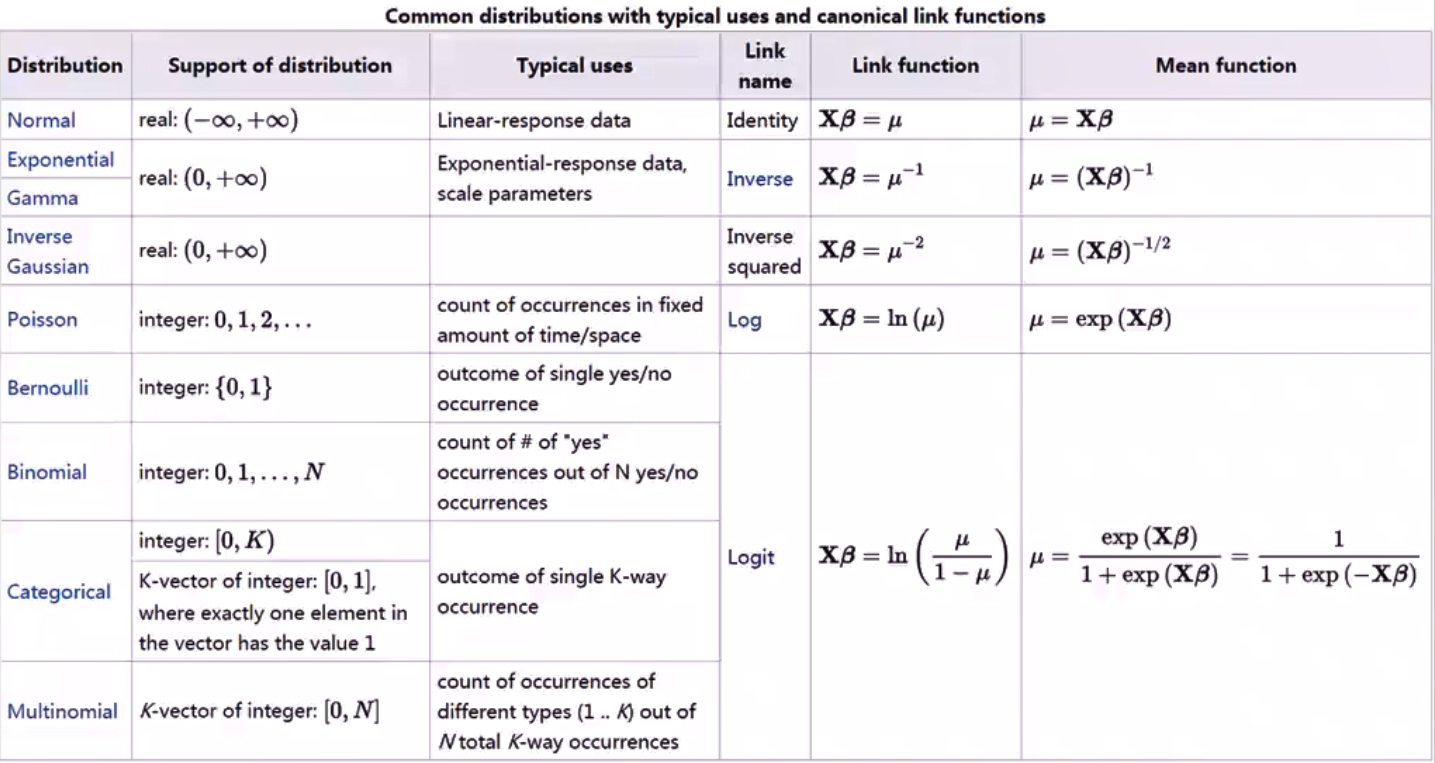
Source
听课笔记
最大似然估计

eg:高斯分布的最大似然估计流程:
步骤:1、知道一个概率密度函数

2、把样本值代入,累乘起来得到\(L(x)\)
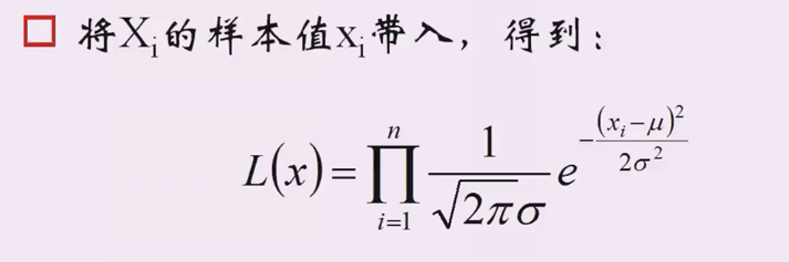
3、对\(L(x)\)取对数,把累乘变成累加
\(l(x)\)为\(ln(L(x))\)
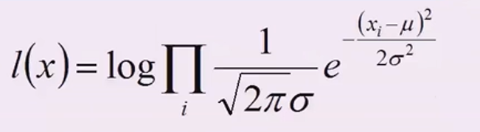
变成求和
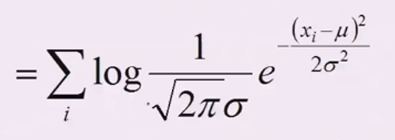
\(e^{????}\)和左边的分数也可以拆开,然后\(ln(e^{????})={????}\)
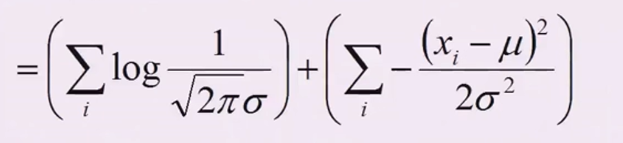
左边里面等价于\(({2\pi\sigma^2})^{-{\frac{1}{2}}}\),把负二分之一拿下来求和
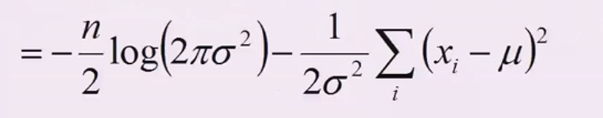
这样就得到了\(f(\mu,\sigma^2)\)
4、\(f(\mu,\sigma^2)\)分别对\(\mu\)和\(\sigma\)求偏导,然后令导后的式子为0,分别解出\(\mu\)和\(\sigma\)
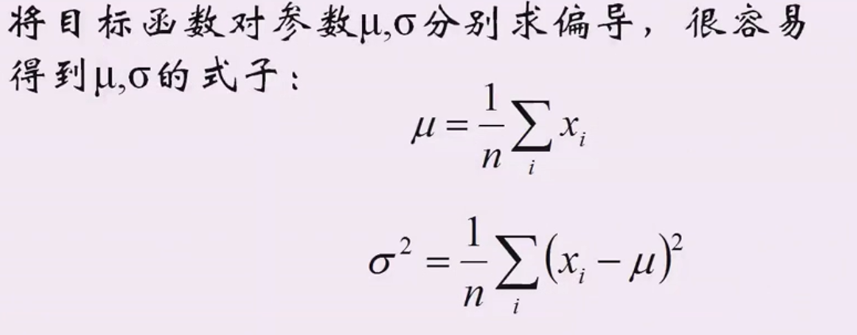
PCA(Principal Component Analysis)
即主成分分析方法,是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴,我们发现,大部分方差都包含在前面k个坐标轴中,后面的坐标轴所含的方差几乎为0。于是,我们可以忽略余下的坐标轴,只保留前面k个含有绝大部分方差的坐标轴。事实上,这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,实现对数据特征的降维处理。(source)
方差尽可能大的结果是降维后的数据离散程度更大,分类效果更好。
中心化
数据的中心化是指原数据减去改组数据的平均值,经过中心化处理后,原数据的坐标平移至中心点(0,0),该组数据的均值变为0,以此也被称为零均值化。
求方差
X为样本矩阵,\(\overrightarrow{u}\)为投影方向
假设\(X \cdot u\)已经中心化(即\((Xu-E)\)中\(E=0\)):
\(Var = (Xu)^T \cdot(Xu) = u^T \cdot X^T \cdot X\cdot u\)
One-hot编码
一个特征有很多个值,我们可以用one-hot编码把这个特征分成很多个特征。
举个和onehot编码有点像的例子,下面是38译码器的真值表和电路图(

左边每个输入的值代表这个特征里面不同的值(也可以是区间),假设把这个特征分成了8个特征,那么每个值(区间)就对应一个y的值为1,其他y为0。
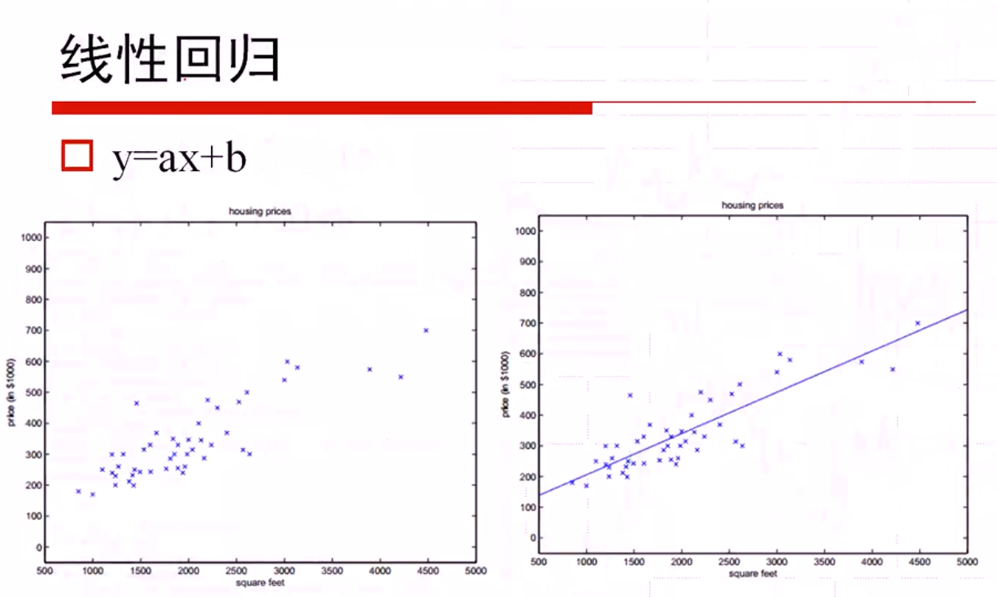
线性回归
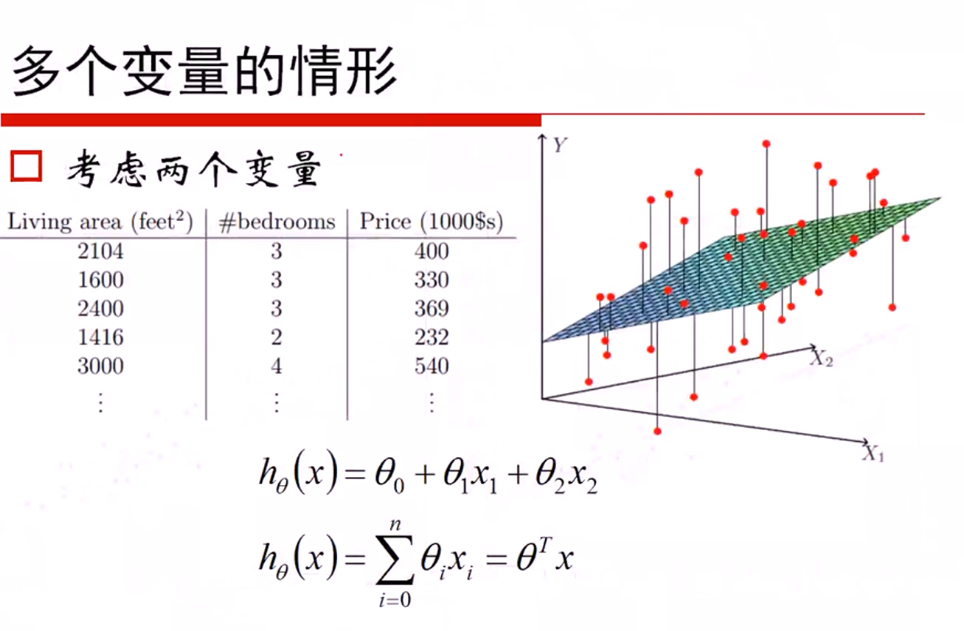
高斯分布的对数似然与最小二乘:
残差高斯分布,得到概率密度函数:
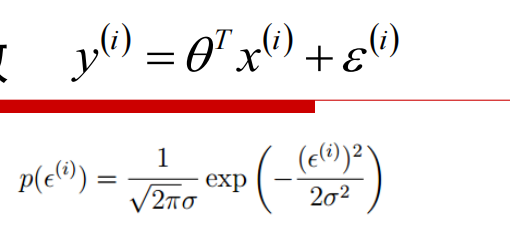
将\(\epsilon\)用\(y 、\theta、x\)替换
然后求似然函数(联合概率密度)
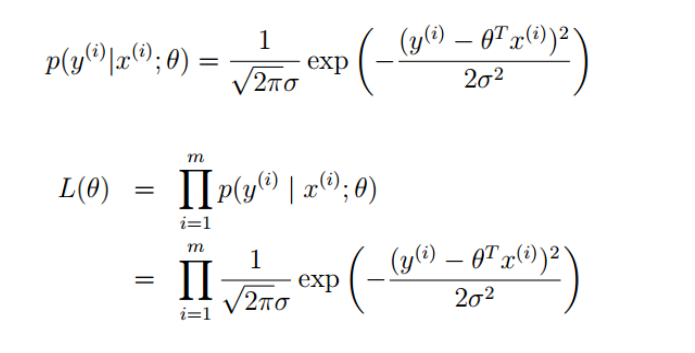
左右取对数,进行化简
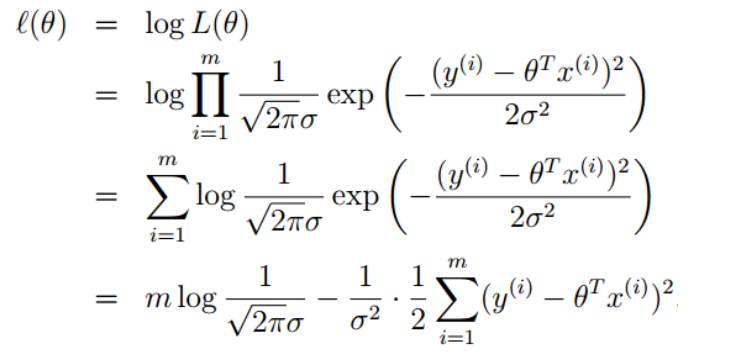
要让\(l(\theta)\)最大,即让右边那一块最小(左半部分都与\(\theta\)无关)
将减号放入右边:
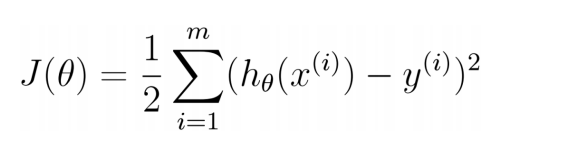
与最小二乘法的公式比较

注:不是搞高斯分布则不能使用最小二乘法,要对模型进行改造,增加特征使得其变成高斯分布
上式又可以写成:
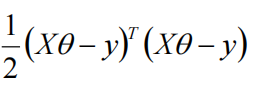
然后对其求梯度:
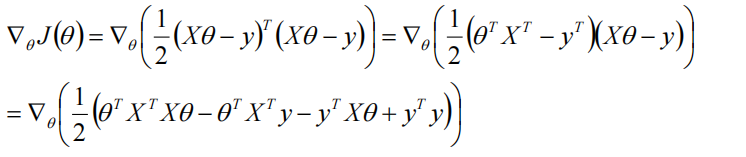
对\(\theta\)求偏导:
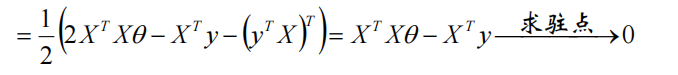
令\(X^TX\theta - X^Ty = 0\)求驻点
如果\({(XX^T)}^{-1}\)可逆
则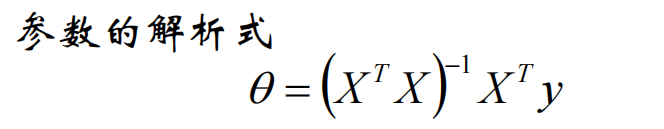
不可逆阵加上单位阵以后就可以求逆了(加上超参数\(\lambda \cdot I\)):
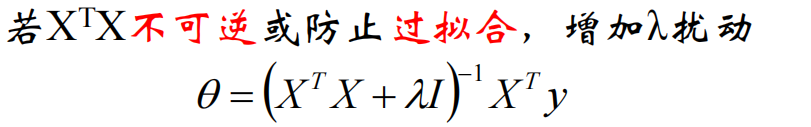
\(\lambda > 0\)
为了防止过拟合,加上损失,得到了L2-norm(ridge):
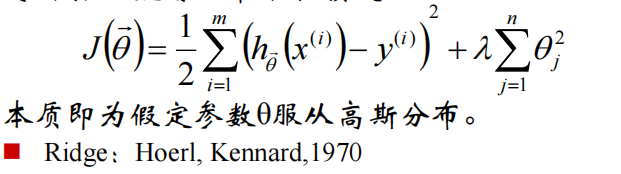
\(\lambda > 0\)
如果加上的是\(\sum{| \theta |}\),则为L1-norm(LASSO):

\(\lambda > 0 \quad and \quad \rho \in [0,1]\)
它两各取一部分,组成弹性网(Elastic Net):
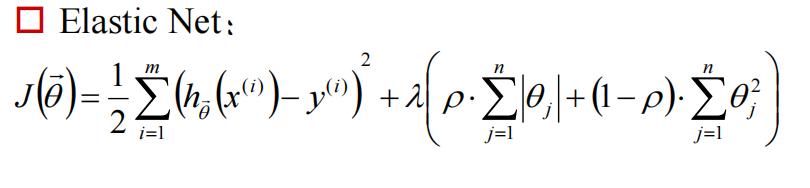
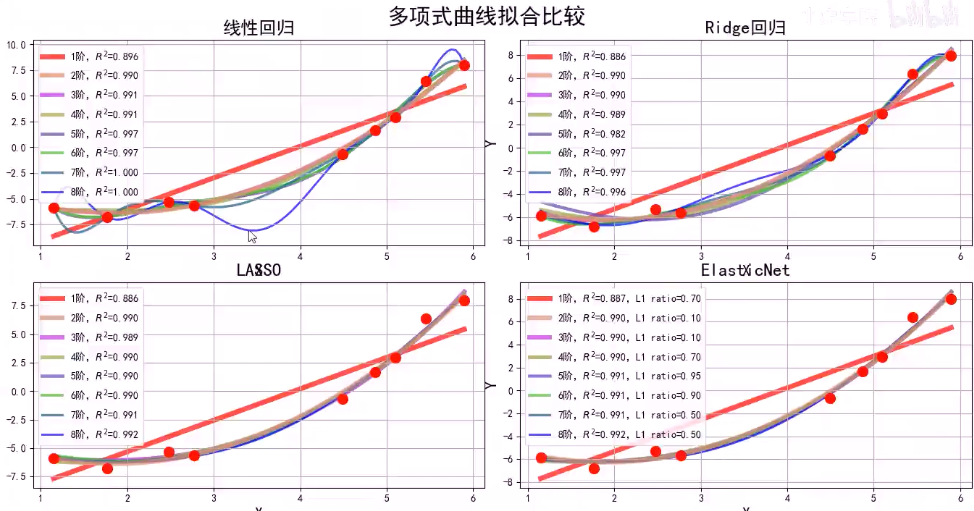
那么超参数怎么选择呢?用验证集(validation set)
如下图所示,用训练集通过之前提到的公式得到参数\(\theta\),\(\theta\)的表达式中包含有超参数\(\lambda\),将\(\lambda\)代入后用验证数据验证哪个\(\lambda\)更优(如果是最小二乘法得到的参数,则取与真实值差的平方和最小)。

梯度下降的一个引入
首先举个栗子:
如果要找到\(f(x)=cosx\)的极小值点,我们除了求导以外,还能梯度下降:
假设当前\(x=5\),沿着梯度sinx方向每次前进 \(learning\_rate*sinx\):
import numpy as np
n = 1000
learning_rate = 0.1
x = 5
for i in range(0,1000):
x += np.sin(x) * learning_rate
print(i,x)
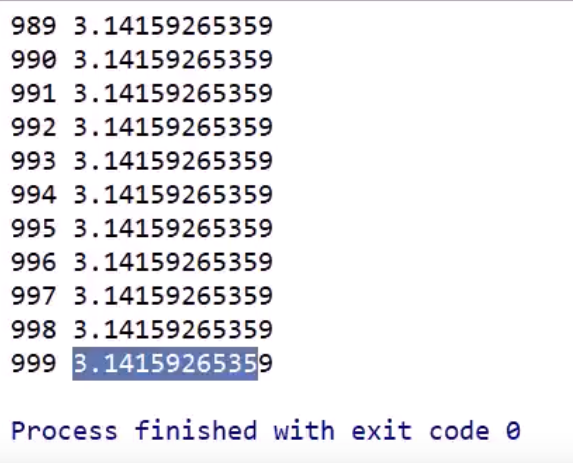
这样就通过梯度下降找到了\(x=5\)时\(cosx\)取最小值时\(x\)的取值。
把所有样本的梯度加起来的话,就是批量梯度下降:

如果取若干样本求梯度做梯度下降,则称为随机梯度下降(SGD):

如果不是每拿到一个样本即更改梯度,而是若干个样本的平均梯度作为更新方向,则是mini-batch梯度下降算法。
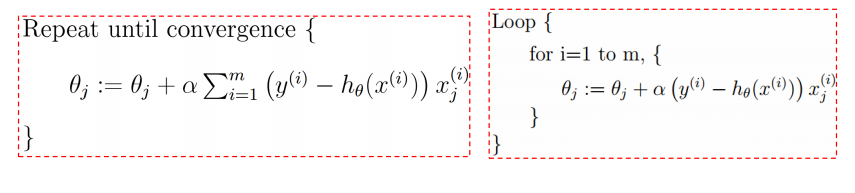
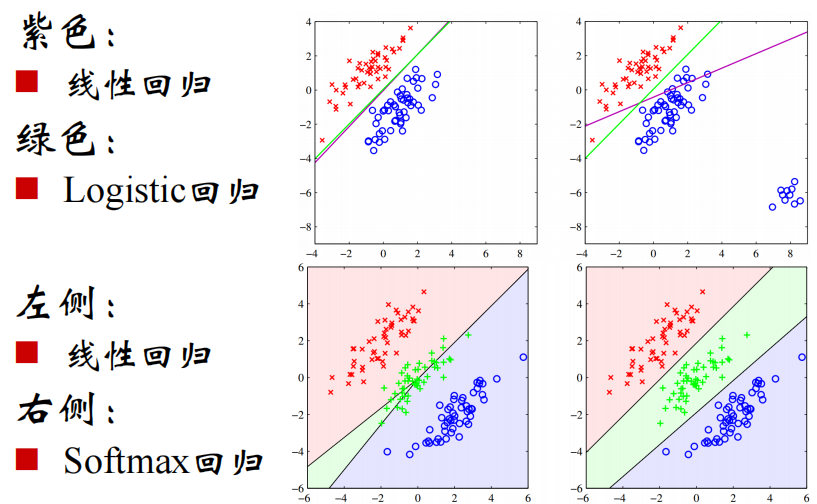
Logistic回归
logistic回归是分类的首选算法,一般用于二分类
Softmax回归用于多分类
实际应用时可能会用若干个二分类去近似一个多分类
Logistic/sigmoid函数
给这样一个函数(sigmoid函数):
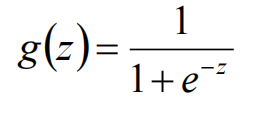
它的图像长这样:
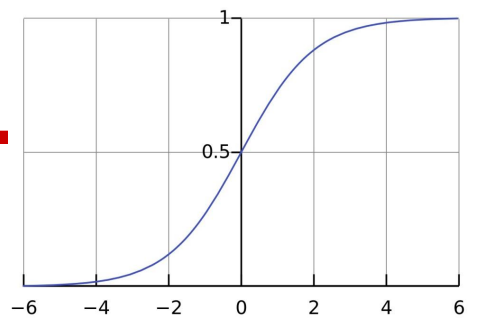
因为它的值域是(0,1),且图像是这样,所以可以以0.5作为阈值做二分类:
逻辑回归的模型:
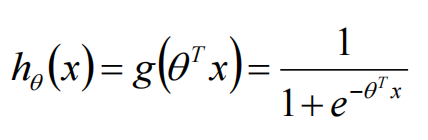
机器学习要做的一件最重要的事:选择一个合适模型(model),再选择一个模型的损失函数(loss)
线性回归时的损失函数(假定为高斯分布求最大似然估计得到的):\(\frac{1}{m}\sum(\hat{y}_i-y_i)^2\)
在logistic回归中对于\(h_{\theta}(x)\):
假定它为两点分布
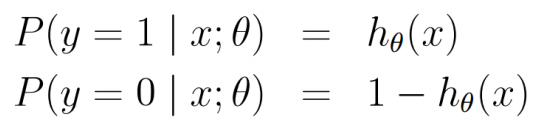
上式也可以写成:
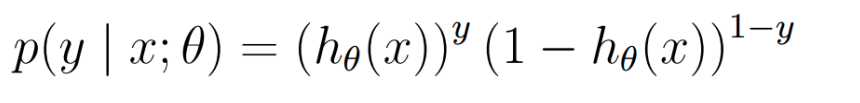
联乘所有样本的概率密度函数得到联合概率密度(似然函数\(L(\theta)\)):
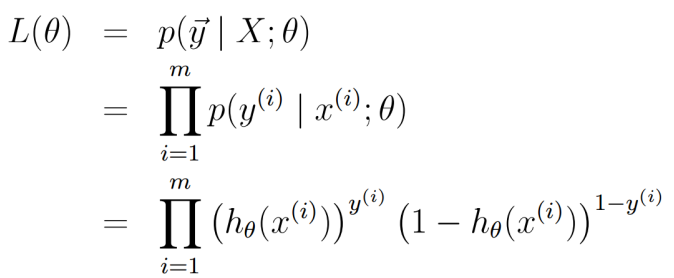
左右取对数:
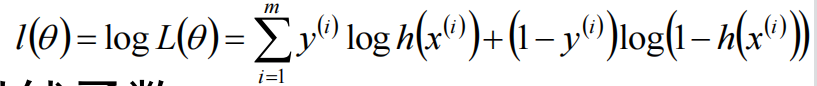
对\(\theta\)求偏导:
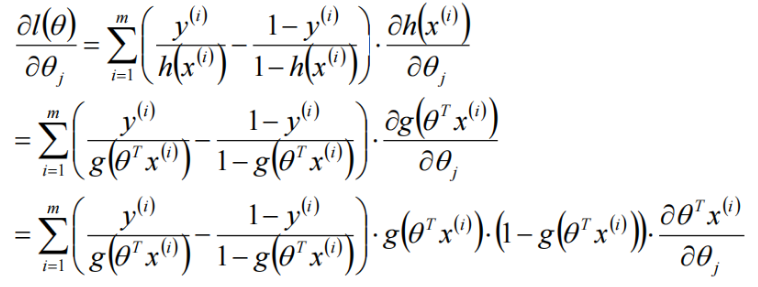
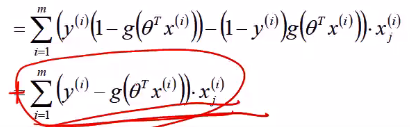
对loss进行梯度下降(上升、正梯度下降()),得到logistic回归参数的学习规则:
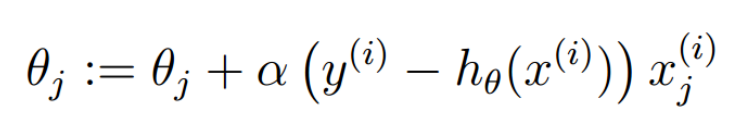
与线性回归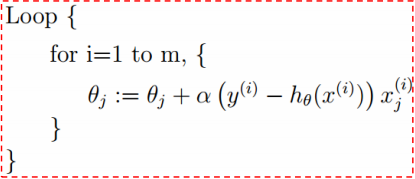 比较,他们具有相同的形式
比较,他们具有相同的形式
对数线性模型
一个事件的几率odds,是指该事件发生的概率与该事件不发生的概率的比值。这个几率取对数,即logit函数:
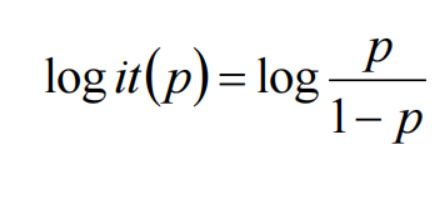
将logistic回归模型代入:
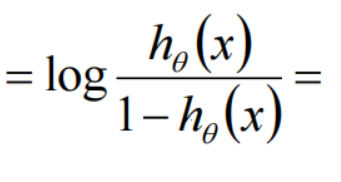
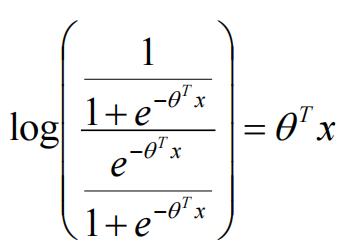
逻辑回归是对数线性模型(广义线性模型),只能得到线性分界面。