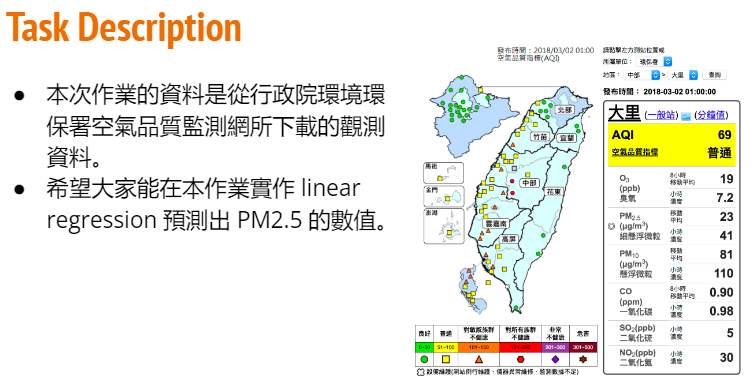
前情提要:


本文刚过strong baseline,入门水平
第一个作业是手写线性回归+梯度下降预测PM2.5,某acm退役人终于不能拿不会sklearn当做不写的理由了(((
当然纯C++选手之前完全没有写过python,也没写过机器学习算法,需要参考课程范例以及一些前人的经验
主要参考课程样例,差不多是跟着这个做的(为什么进不去懂的都懂)

数据集

每个月记录20天,每天记录20个小时,总共有18个特征(PM2.5包括在其中)
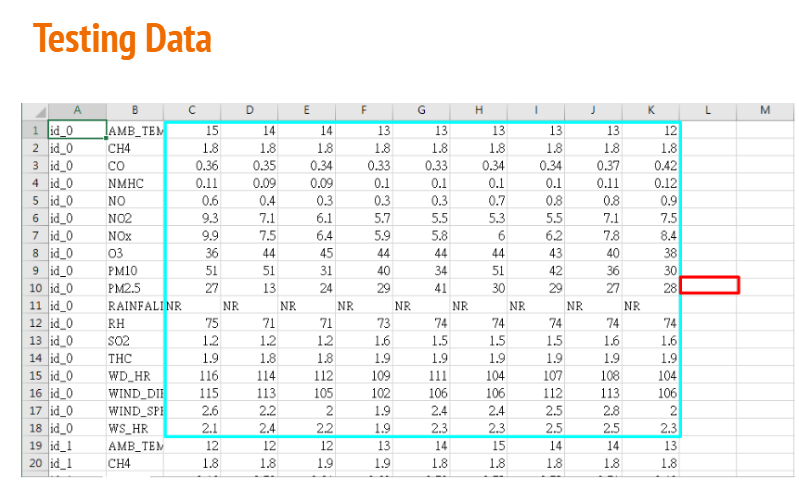
需要用前9个小时预测第十个小时的PM2.5监测值
数据预处理
首先读取数据集
import pandas as pd
import numpy as np
data = pd.read_csv(r"./train.csv")
发现读了个倒着的进来(读了繁体字),但.columns和.values没有问题,那数据也没问题,可以用朴素的代码去解决这个问题(
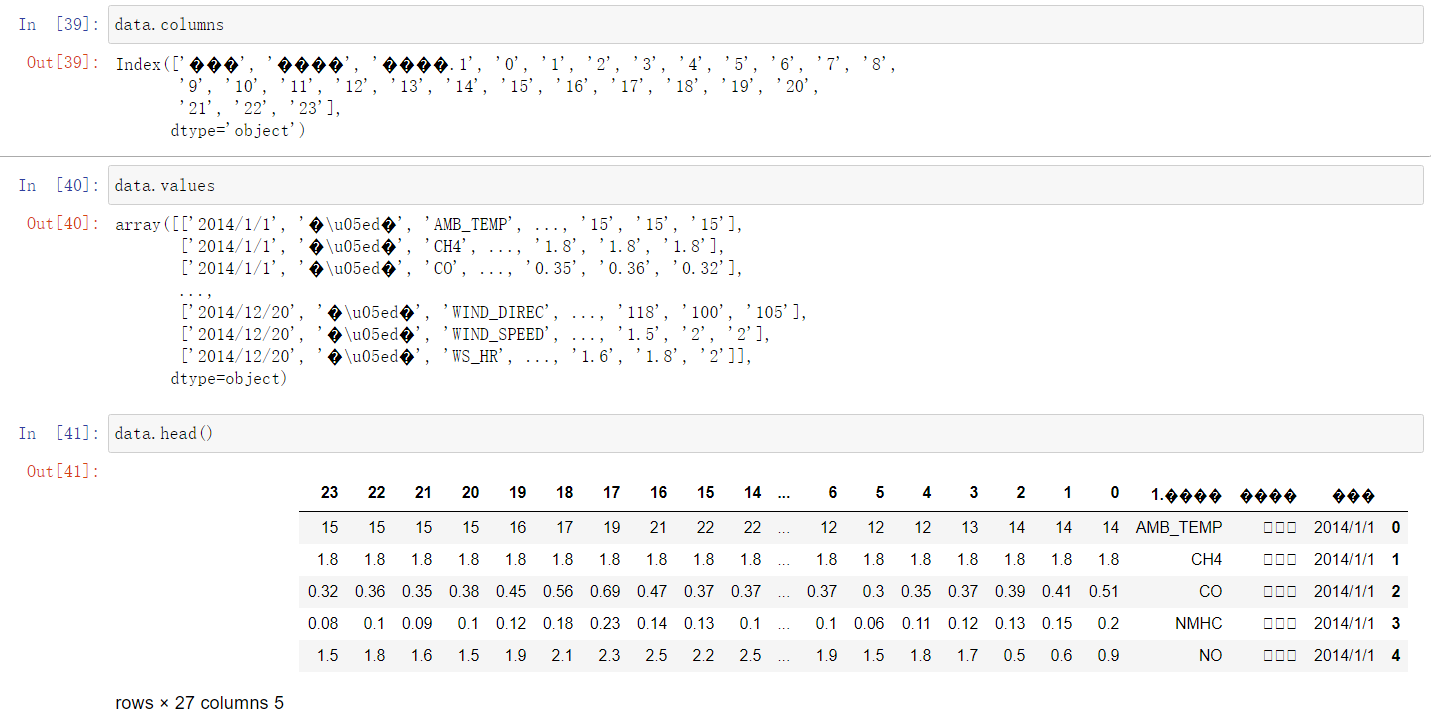
尝试着把有问题的列名改了,然后就好了:
data.rename(columns={data.columns[0]:'日期',data.columns[1]:'测站',data.columns[2]:'测项'},inplace=True)
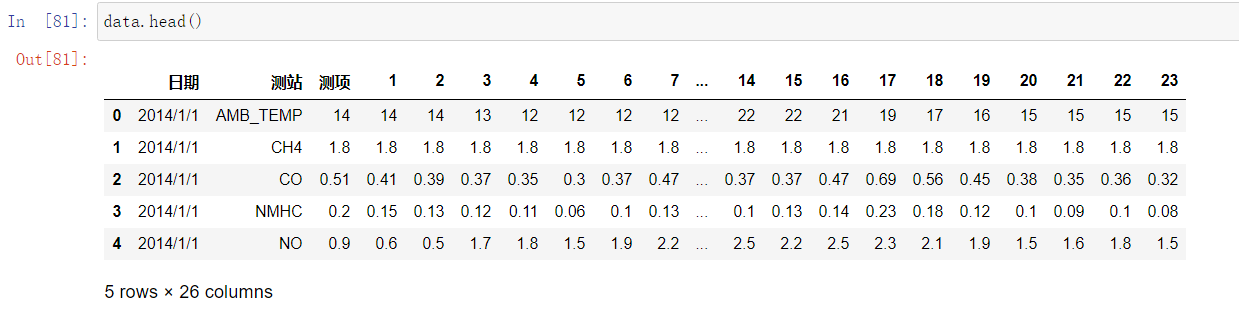
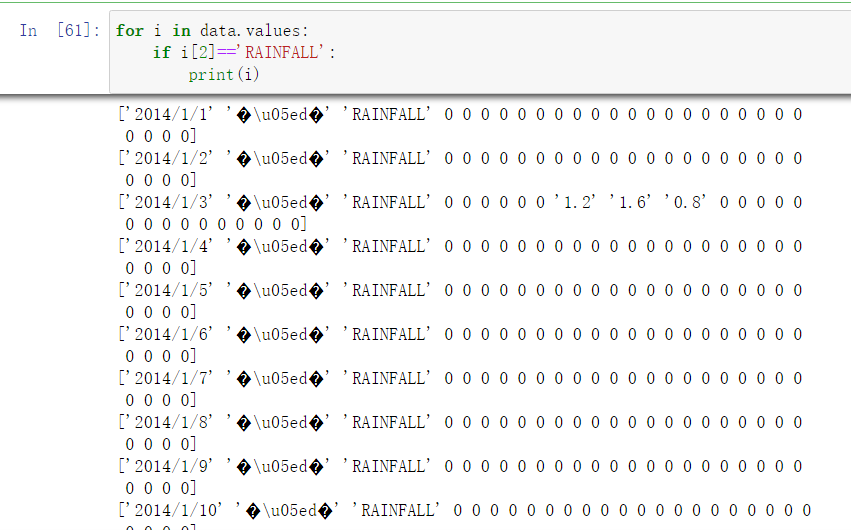
首先把RAINFALL里面的数据看看:
s = set()
for i in range(0,len(data.values)):
if data.values[i][2]=='RAINFALL':
for j in range(3,len(data.values[i])):
s.add(data.values[i][j])

发现除了'NR'以外其他均为实数,把'NR'变成0
#data[data == 'NR'] = 0
for i in range(0,len(data.values)):
if data.values[i][2] == 'RAINFALL':
for j in range(3,len(data.values[i])):
if data.values[i][j] == 'NR':
data.values[i][j] = 0
这样就把RAINFALL里面的非实数消除了
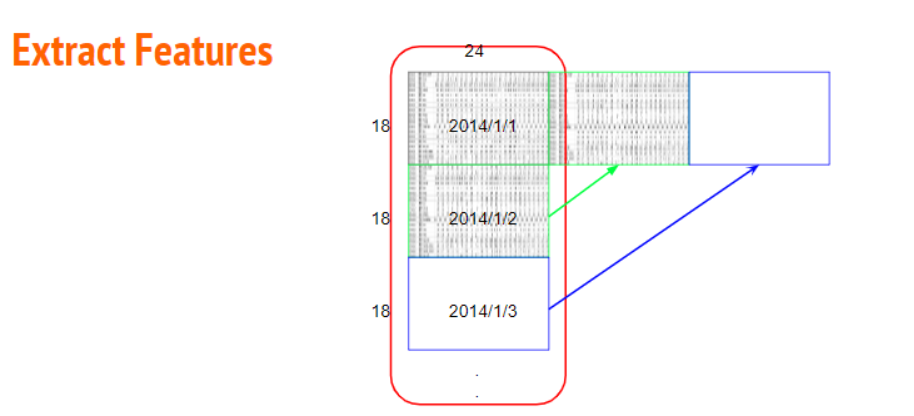
然后就是对表格中特征的提取了。
9个小时里总共的特征数为\(9*18=162\),目标值为第10个小时的PM2.5
对于每一天我们有24个小时的观测数据\([0h,23h]\)
一个月观测20天,也就是480小时(\([0h,479h]\)),总共有特征\(18*480 = 23040\)个。
那么只取\([0h,8h]\&[10h,18h]\&[20h,28h]\)。。。作为\(x\),而选取\(9h\)、\(19h\)、\(29h\)。。。的PM2.5作为\(y\)。这样选取样本是不是太少了?每天只有2组样本(最多3组)
解决方案是通过滑动窗口选取:\([0h,8h] + 9h\)、\([1h,9h] + 10h\)、\([2h,10h] + 11h\)、\([3h,11h] + 12h\)。。。。。。
这样一个月480个小时,我们就可以选取\(480-9 = 471\)组样本了(由于只观测20天,与下个月时间上不连续,所以只取到\([470,478] + 479h\))
官方的范例图示就是上面表达意思(一年12个月,也就是\(18*480*12\),数据只给了2014年):

接下来就是代码实现了
想到要把数据分成\(12\)组,每组\(18*480\),原表格中格式好像完全规整,那就没时间、特征名啥事了
1、只留下数据列
data = data.iloc[:,3:]
raw_data = data.to_numpy()

2、分组(把每个月的数据块(二维数组)放入字典)
开一个字典,保存每个月的观测值(过程如下图)
month_data={}
for month in range(12):
tmp = np.empty([18,480]) # 创建18*480的二维数组
for day in range(20):
tmp[:, 24 * day : 24 * (day + 1)] = raw_data[18 * (month * 20 + day):18 * (month * 20 + day + 1),:]
month_data[month] = tmp
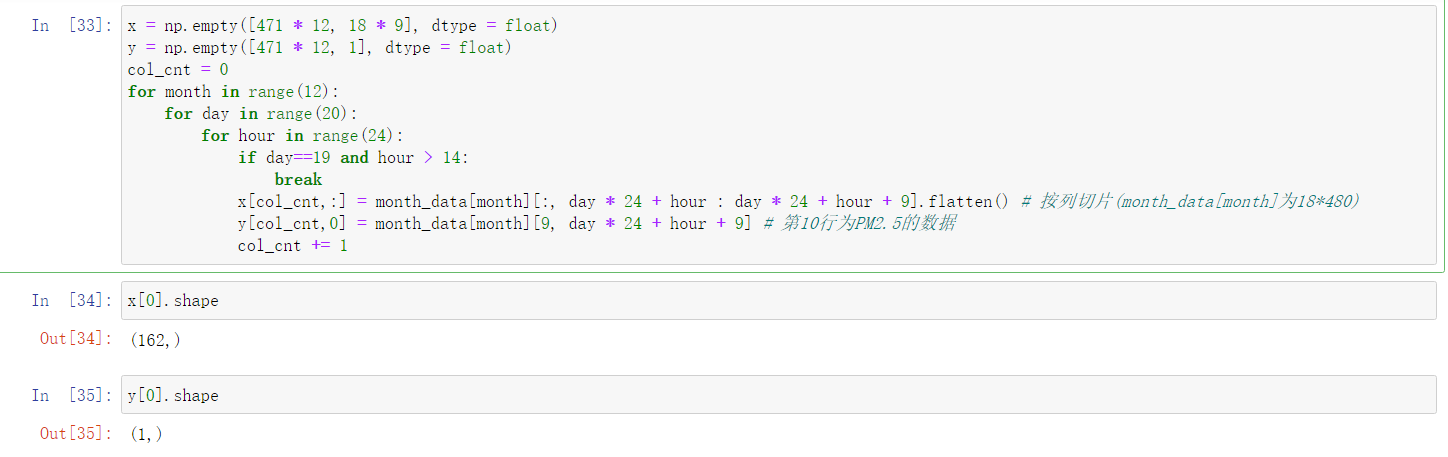
3、滑动窗口取特征
首先构造数组:
对于x数组:有18个特征,每组有9个小时,因此有\(18 * 9 = 162\)列;总共有12个月,每个月可以取471组(480-9=471,之前写了为什么),因此有\(12 * 471\)行
对于y数组:当然只有1列,即目标值"第十小时的PM2.5";行数与x数组相同
x = np.empty([471 * 12, 18 * 9], dtype = float)
y = np.empty([471 * 12, 1], dtype = float)
col_cnt = 0
for month in range(12):
for day in range(20):
for hour in range(24):
if day==19 and hour > 14:
break
x[col_cnt,:] = month_data[month][:, day * 24 + hour : day * 24 + hour + 9].flatten() # 按列切片(month_data[month]为18*480)
y[col_cnt,0] = month_data[month][9, day * 24 + hour + 9] # 第10行为PM2.5的数据
col_cnt += 1
这样我们就完成了数据的预处理,得到x数组和y数组
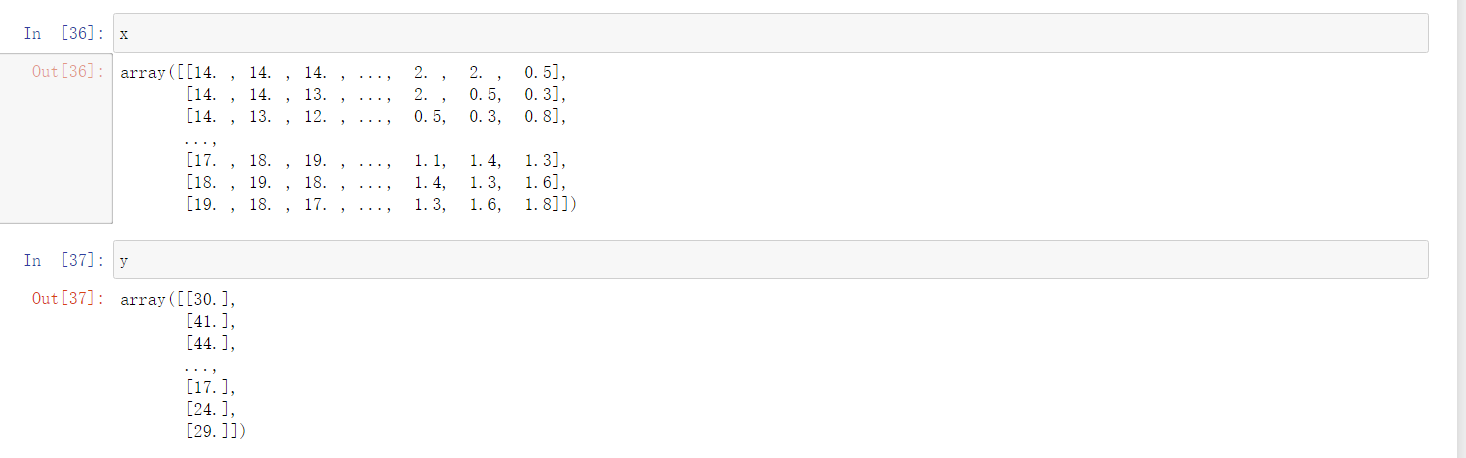
Normalize
特征工程中的「归一化」有什么作用?- 知乎
采用的是Z-score(零均值规范化): \(X_{after} = \frac{X - X_{mean}}{\sigma}\)
标准化后的变量值围绕0上下波动,大于0说明高于平均水平,小于0说明低于平均水平。
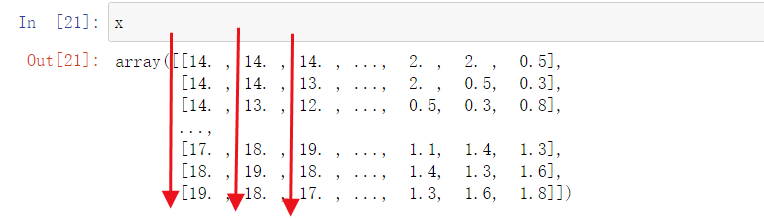
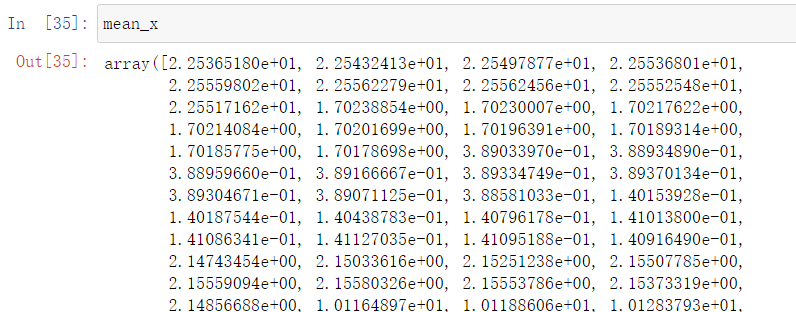
mean_x = np.mean(x, axis=0) # 按列(竖着求均值)
std_x = np.std(x, axis=0) # 标准差同上
然后进行normalize
for i in range(len(x)):
for j in range(len(x[0])):
if std_x[j] != 0: # 不能除0
x[i][j] = (x[i][j]-mean_x[j])/std_x[j]

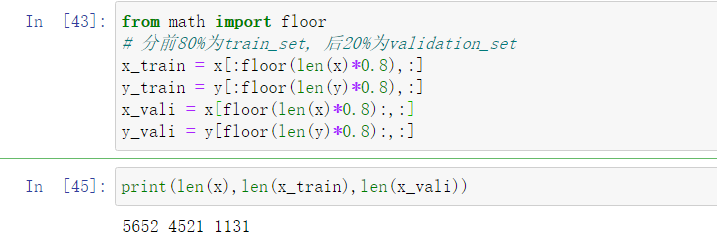
Split training data into "train" and "validation"
有现成的sklean.train_test_split可以用
from math import floor
# 分前80%为train_set, 后20%为validation_set
x_train = x[:floor(len(x)*0.8),:]
y_train = y[:floor(len(y)*0.8),:]
x_vali = x[floor(len(x)*0.8):,:]
y_vali = y[floor(len(y)*0.8):,:]
Train
先解释这个图什么意思:
对于每次迭代,\(y' = x \cdot w\),然后得到\(Loss = y' - y\),
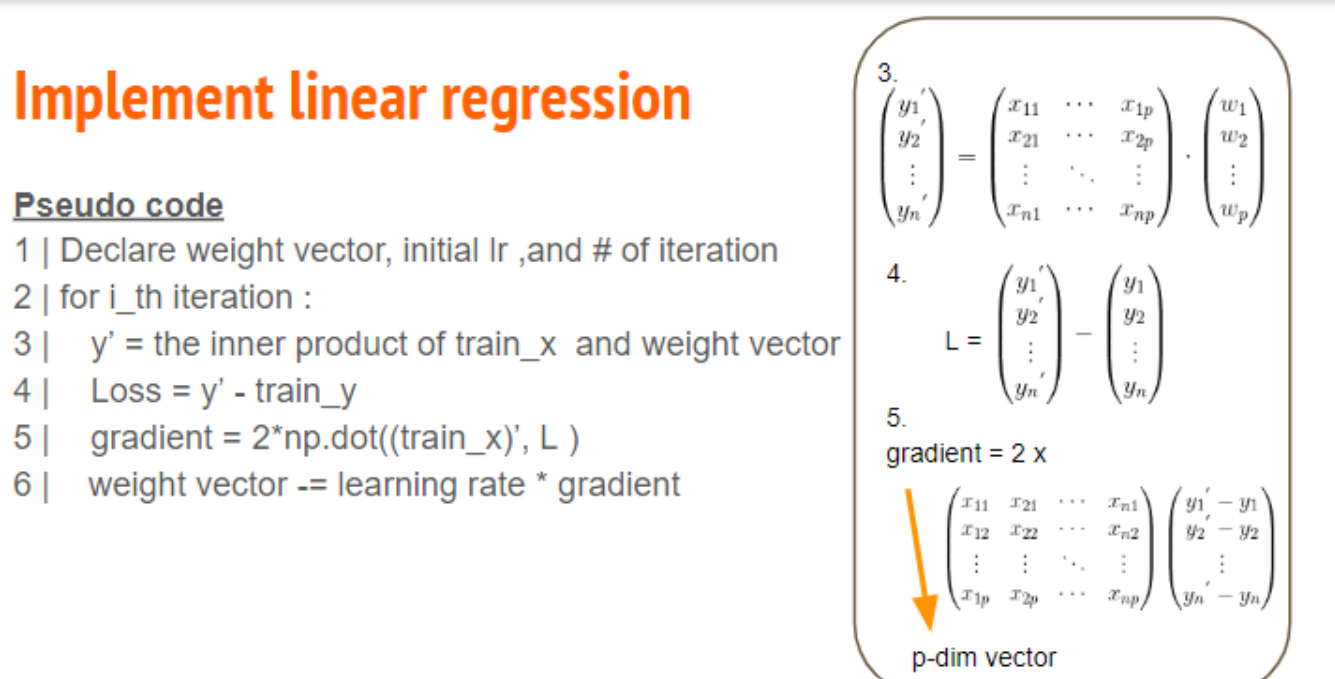
gradient为\(2x^T \cdot Loss\)(如下),
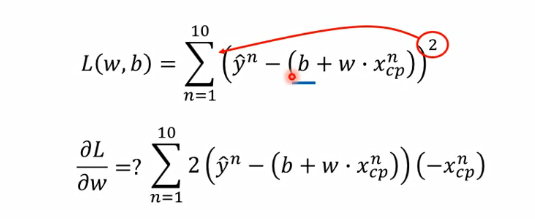
然后让\(w_{i+1} = w_i - {learning\_rate} * gradient\)
不过样例演示使用的是adgrad算法:
该算法的思想是独立地适应模型的每个参数:具有较大偏导的参数相应有一个较大的学习率,而具有小偏导的参数则对应一个较小的学习率 具体来说,每个参数的学习率会缩放各参数反比于其历史梯度平方值总和的平方根
伪代码如下:

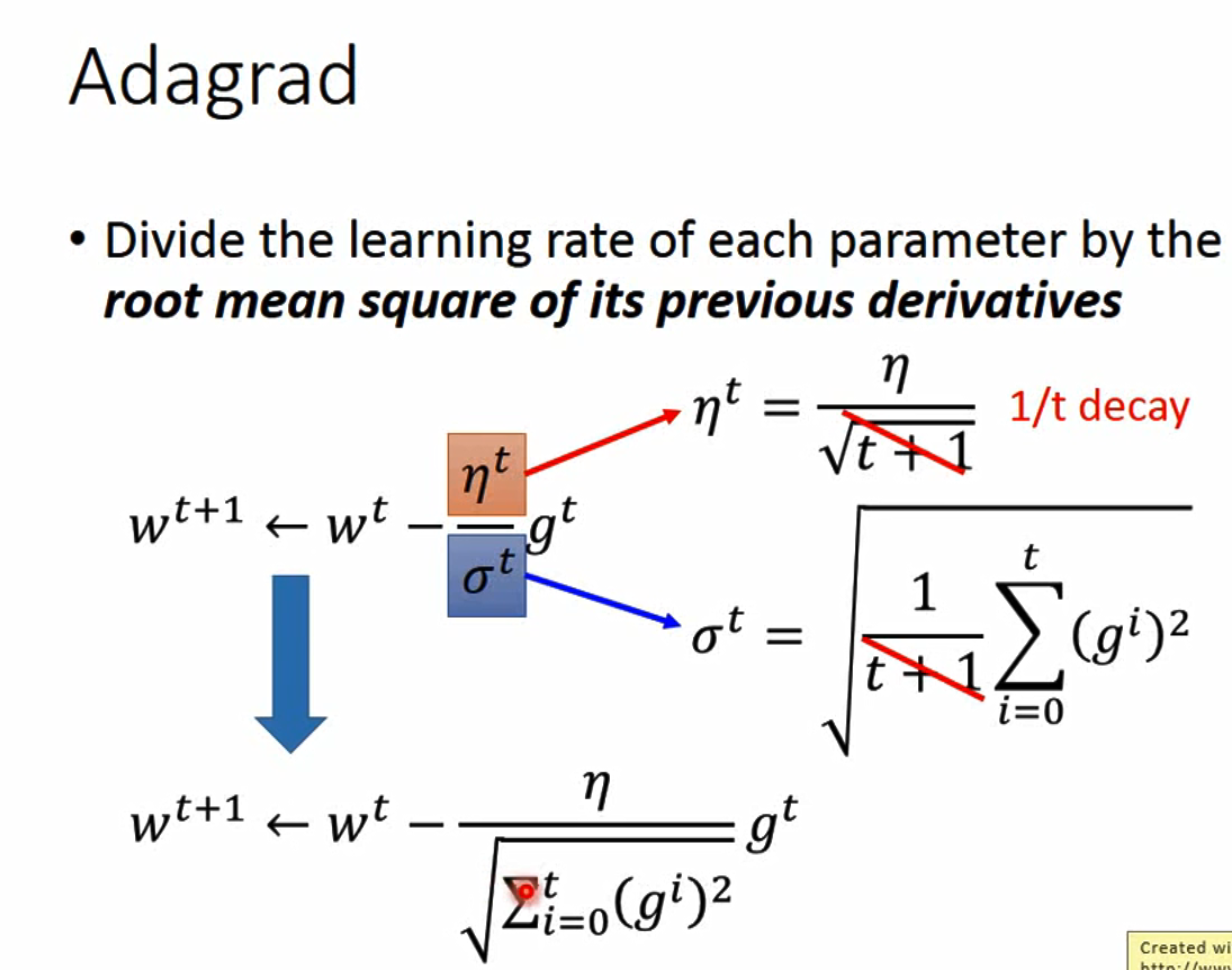
对于每次迭代,前面的步骤一直到5.1都和之前没有区别(但代码里Loss改为了均方根误差rmse:\(rmse = \sqrt{\frac{1}{m} \sum\limits_{i=1}^{m}(y_i-\hat{y_i})^2}\))
然后令\(prev\_grad\) += \(gradient^2\),\(ada = \sqrt{prev\_gra}\)
最后\(w_{i+1} = w_i - \frac{{learning\_rate} * gradient}{ada}\)
其中\(prev\_grad\)初始化为一个全1的与\(gradient\)维数相同的向量
dim = 18 * 9 + 1 # 维度dimension,加上1个常数项
w = np.zeros([dim,1]) # dim行1列,全部填0
pregrad = np.zeros([dim, 1])
x = np.concatenate((np.ones([12 * 471, 1]), x), axis = 1).astype(float) # 同样每一行补上常数项
learning_rate = 100 # 学习率
iter_time = 1000 # 迭代次数
eps = 1e-8 # 避免分母ada为0而加上的极小项
for t in range(iter_time):
loss = np.sqrt(np.sum(np.power(np.dot(x, w) - y, 2))/471/12) # rmse = y - y_hat求和的平方取平均开根号
if(t % 100 == 0):
print(str(t) + ":" + str(loss)) # 查看每100次迭代当前的loss值
gradient = 2 * np.dot(x.transpose(), np.dot(x,w) - y) #套公式
pregrad += gradient ** 2 #套公式
ada = np.sqrt(pregrad + eps) #套公式
w = w - learning_rate * gradient / ada #套公式
np.save('weight.npy', w) # 可以将w保存在本地
发现loss(rmse)从27逐渐减小到7

同时得到train结果w:
Testing
首先预处理test_set,流程同train的预处理:
testdata = pd.read_csv("./test.csv",header=None) # 没有列index
test_data = testdata.iloc[:, 2:] # 把id_0和AMB_TEMP去掉
test_data[test_data=='NR'] = 0
test_data = test_data.to_numpy()
test_x = np.empty([240, 18 * 9], dtype = float) # id_0~id_239, 240组测试数据
for i in range(240):
test_x[i, :] = test_data[18 * i:18 * (i + 1), :].flatten()
# Normalize,用之前的mean_x和std_x
for i in range(len(test_x)):
for j in range(len(test_x[0])):
if std_x[j] != 0:
test_x[i][j] = (test_x[i][j]-mean_x[j])/std_x[j]
# 拼常数项的列
test_x = np.concatenate((np.ones([240, 1]), test_x), axis = 1).astype(float)
得到test_x:
Predict
最后一步就是预测了,这一步直接\(y\_test = x\_test \cdot w\)即可
ansy = np.dot(test_x,w)

最后把得到的结果用csv保存即可(不写了直接复制):
import csv
with open('submit.csv', mode='w', newline='') as submit_file:
csv_writer = csv.writer(submit_file)
header = ['id', 'value']
print(header)
csv_writer.writerow(header)
for i in range(240):
row = ['id_' + str(i), ans_y[i][0]]
csv_writer.writerow(row)
print(row)
这样直接提交public只能达到simple baseline

凭借数学直觉,主观感觉需要增加迭代次数和降低学习率,然后过了public的strong baseline:


但不知道private会怎么样,感觉还会有很多优化空间,多上几节课学点东西再回来看看。。。。。。