众所周知,机器学习的训练数据之所以非常昂贵,是因为需要大量人工标注数据。
autoencoder可以输入数据和输出数据维度相同,这样测试数据匹配时和训练数据的输出端直接匹配,从而实现无监督训练的效果。并且,autoencoder可以起到降维作用,虽然输入输出端维度相同,但中间层可以维度很小,从而起到降维作用,形成数据的一个浓缩表示。
可以用autoencoder做Pretraining,对难以训练的深度模型先把网络结构确定,之后再用训练数据去微调。
特定类型的autoencoder可以做生成模型生成新的东西,比如自动作诗等。
data representation:
人的记忆与数据的模式有强烈联系。比如让一位娴熟的棋手记忆某局棋局状态,会显示出超强的记忆力,但如果面对的是一局杂乱无章的棋局,所展现的记忆能力与普通人没什么差别。这体现了模式的力量,可以通过数据间关系进行记忆,效率更高。
autoencoder由于中间层有维度缩减的功效,因而强制它找到一个数据内部的pattern,从而起到高效的对训练数据的记忆作用。
如下图所示,一般中间层选取的维度很小,从而起到高效表示的作用。
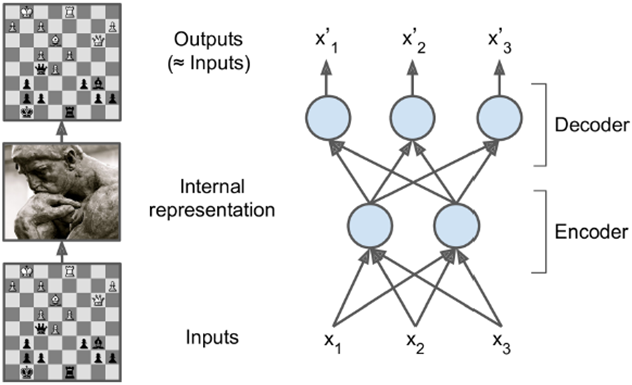
如果完全做线性训练,cost function选取MSE,则这个autoencoder训练出来的效果相当于PCA的效果。
# 建立数据集 rnd.seed(4) m = 200 w1, w2 = 0.1, 0.3 noise = 0.1 angles = rnd.rand(m) * 3 * np.pi / 2 - 0.5 data = np.empty((m, 3)) data[:, 0] = np.cos(angles) + np.sin(angles)/2 + noise * rnd.randn(m) / 2 data[:, 1] = np.sin(angles) * 0.7 + noise * rnd.randn(m) / 2 data[:, 2] = data[:, 0] * w1 + data[:, 1] * w2 + noise * rnd.randn(m) # nomalize 训练集 from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X_train = scaler.fit_transform(data[:100]) X_test = scaler.transform(data[100:]) # 开始建立autoencoder import tensorflow as tf from tensorflow.contrib.layers import fully_connected n_inputs = 3 # 3D inputs n_hidden = 2 # 2D codings # 强制输出层和输入层相同 n_outputs = n_inputs learning_rate = 0.01 X = tf.placeholder(tf.float32, shape=[None, n_inputs]) # 隐层和输入层进行全连接 hidden = fully_connected(X, n_hidden, activation_fn=None) # 不做任何非线性处理,activation=none outputs = fully_connected(hidden, n_outputs, activation_fn=None) # lost function使用均方差MSE reconstruction_loss = tf.reduce_mean(tf.square(outputs - X)) # MSE optimizer = tf.train.AdamOptimizer(learning_rate) training_op = optimizer.minimize(reconstruction_loss) init = tf.global_variables_initializer() # 运行部分 # load the dataset X_train, X_test = [...] n_iterations = 1000 # the output of the hidden layer provides the codings codings = hidden with tf.Session() as sess: init.run() for iteration in range(n_iterations): # no labels (unsupervised) training_op.run(feed_dict={X: X_train}) codings_val = codings.eval(feed_dict={X: X_test})
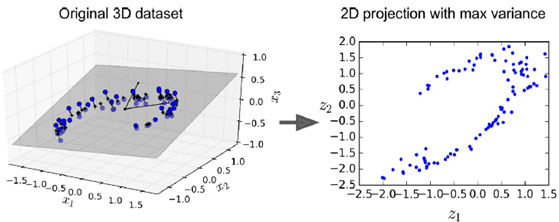
中间隐层作用如下图所示,将左图中3维的图形选取一个最优截面,映射到二维平面上。
stacked autoencoder
做多个隐层,并且输入到输出形成一个对称的关系,如下图所示,从输入到中间是encode,从中间到输出是一个decode的过程。
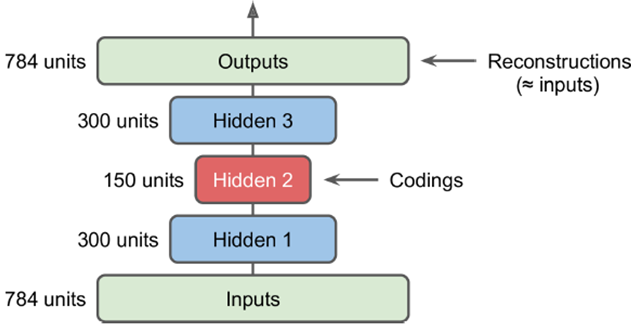
但层次加深后,训练时会有很多困难,比如如下代码中,使用l2的regularization来正则化,使用ELU来做激活函数
n_inputs = 28 * 28 # for MNIST n_hidden1 = 300 n_hidden2 = 150 # codings n_hidden3 = n_hidden1 n_outputs = n_inputs learning_rate = 0.01 l2_reg = 0.001 X = tf.placeholder(tf.float32, shape=[None, n_inputs]) # arg_scope相当于对fully_connected这个函数填公共参数,如正则化统一使用l2_regularizer等,则以下4个fully_connected的缺省参数全部使用with这里写好的 with tf.contrib.framework.arg_scope( [fully_connected], activation_fn=tf.nn.elu,
weights_initializer=tf.contrib.layers.variance_scaling_initializer(),
weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg)): hidden1 = fully_connected(X, n_hidden1) hidden2 = fully_connected(hidden1, n_hidden2) # codings hidden3 = fully_connected(hidden2, n_hidden3) # 最后一层用none来覆盖之前缺省的参数设置 outputs = fully_connected(hidden3, n_outputs, activation_fn=None) # 由于之前使用了正则化,则之后可以直接把中间计算的loss从REGULARIZATION_LOSSES中提取出来,加入到reconstruction_loss中 reconstruction_loss = tf.reduce_mean(tf.square(outputs - X)) # MSE reg_losses = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES) loss = tf.add_n([reconstruction_loss] + reg_losses) optimizer = tf.train.AdamOptimizer(learning_rate) training_op = optimizer.minimize(loss) init = tf.global_variables_initializer() n_epochs = 5 batch_size = 150 with tf.Session() as sess: init.run() for epoch in range(n_epochs): n_batches = mnist.train.num_examples // batch_size for iteration in range(n_batches): X_batch, y_batch = mnist.train.next_batch(batch_size) # 只提供了x值,没有标签 sess.run(training_op, feed_dict={X: X_batch})
既然autoencoder在权重上是对称的,则权重也是可以共享的,相当于参数数量减少一半,减少overfitting的风险,提高训练效率。
常见的训练手段是逐层训练,隐层1训练出后固定权值,训练hidden2,再对称一下(hidden3与hidden1完全对应),得到最终训练结果
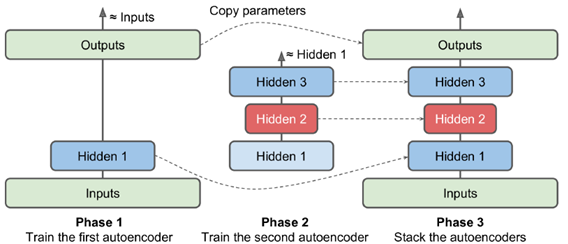
或者可以定义不同的name scope,在不同的phase中训练,
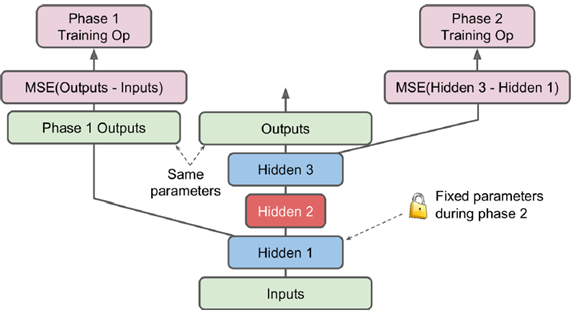
[...] # Build the whole stacked autoencoder normally. # In this example, the weights are not tied. optimizer = tf.train.AdamOptimizer(learning_rate) with tf.name_scope("phase1"): phase1_outputs = tf.matmul(hidden1, weights4) + biases4 phase1_reconstruction_loss = tf.reduce_mean(tf.square(phase1_outputs - X)) phase1_reg_loss = regularizer(weights1) + regularizer(weights4) phase1_loss = phase1_reconstruction_loss + phase1_reg_loss phase1_training_op = optimizer.minimize(phase1_loss) # 训练phase2时,phase1会冻结 with tf.name_scope("phase2"): phase2_reconstruction_loss = tf.reduce_mean(tf.square(hidden3 - hidden1)) phase2_reg_loss = regularizer(weights2) + regularizer(weights3) phase2_loss = phase2_reconstruction_loss + phase2_reg_loss train_vars = [weights2, biases2, weights3, biases3] phase2_training_op = optimizer.minimize(phase2_loss, var_list=train_vars)
Pretraining
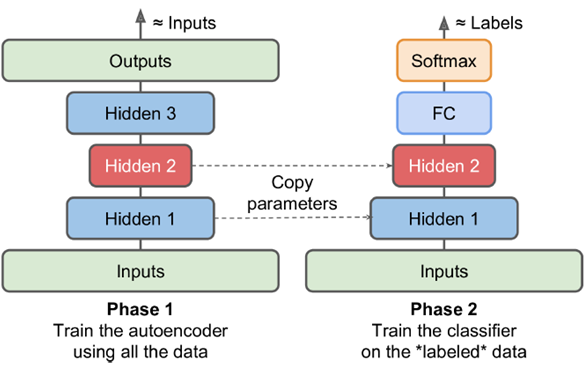
若大量数据无label,少量数据有label,则用大量无label数据在第一阶段作无监督的Pretraining训练,将encoder部分直接取出,output部分做一个直接改造。减少由于有label数据过少导致的过拟合问题。比如下图中的fully connected,和输出的softmax。
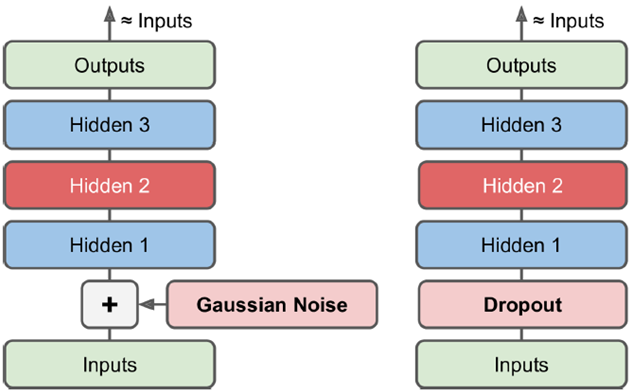
去噪(denoising Autoencoder)
如下的强制加入噪声,最后学到的是不带噪声的结果。并且训练时可以加入dropout层,拿掉一部分网络结构(测试时不加)。这些都可以增加训练难度,从而增进网络鲁棒性,让模型更加稳定。
sparse Autoencoder
中间层激活神经元数量有一个上限阈值约束,中间层非常稀疏,只有少量神经元有数据,正所谓言简意赅,这样可以增加中间层对信息的概括表达能力。
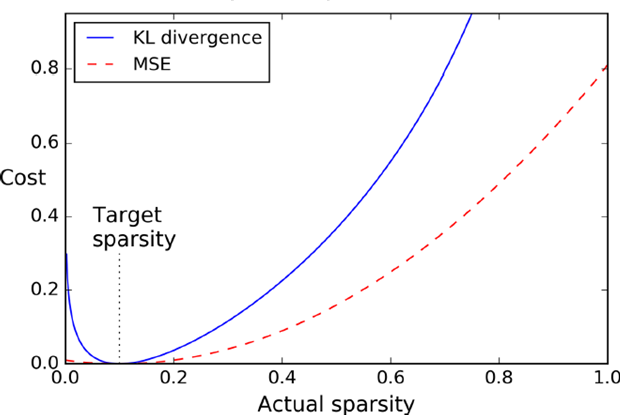
第一种加入平方误差,第二种KL距离,如下图可以看出KL距离![]() 和MSE之间差别比较。
和MSE之间差别比较。
def kl_divergence(p, q): return p * tf.log(p / q) + (1 - p) * tf.log((1 - p) / (1 - q)) learning_rate = 0.01 sparsity_target = 0.1 sparsity_weight = 0.2 [...] # Build a normal autoencoder (the coding layer is hidden1) optimizer = tf.train.AdamOptimizer(learning_rate) hidden1_mean = tf.reduce_mean(hidden1, axis=0) # batch mean sparsity_loss = tf.reduce_sum(kl_divergence(sparsity_target, hidden1_mean)) reconstruction_loss = tf.reduce_mean(tf.square(outputs - X)) # MSE loss = reconstruction_loss + sparsity_weight * sparsity_loss training_op = optimizer.minimize(loss) # kl距离不能取0值,因而不能使用tann的激活函数,故选取(0,1)的sigmoid函数 hidden1 = tf.nn.sigmoid(tf.matmul(X, weights1) + biases1) # [...] logits = tf.matmul(hidden1, weights2) + biases2) outputs = tf.nn.sigmoid(logits) reconstruction_loss = tf.reduce_sum( tf.nn.sigmoid_cross_entropy_with_logits(labels=X, logits=logits))
Variational Autoencoder
通过抽样决定输出,使用时体现概率的随机性。是一个generation,同训练集有关,但只是类似,是一个完全新的实例。
如下图,中间层加了一个关于分布均值方差的超正态分布的噪声,从而中间学到的不是简单编码而是数据的模式,使得训练数据与正态分布形成一个映射关系,这样输出层可以输出和输入层非常相像但又不一样的数据。
使用时把encoder去掉,随机加入一个高斯噪声,在输出端可以得到一个完全新的输出。
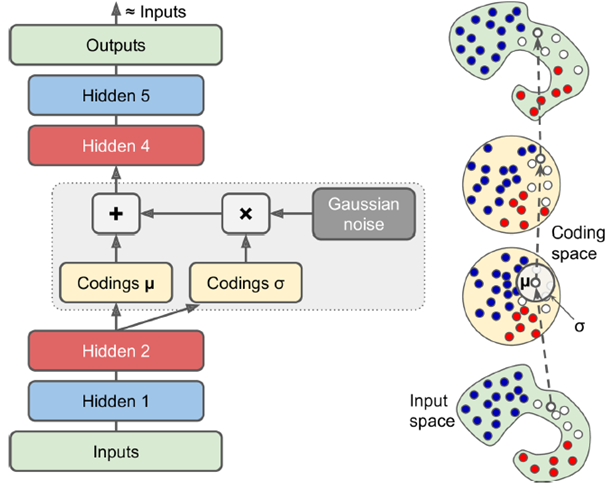
即input通过NN Encoder之后生成两个coding,其中一个经某种处理后与一个高斯噪声(即一系列服从正态分布的噪声)相乘,和另一个coding相加作为初始的中间coding。下图与上图同理,最终生成的output要最小化重构损失,即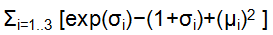 越接近0越好。
越接近0越好。

# smoothing term to avoid computing log(0) eps = 1e-10 # 对原输入空间,通过最小化loss,将原本数据映射到规律的正态分布中 latent_loss = 0.5 * tf.reduce_sum( tf.square(hidden3_sigma) + tf.square(hidden3_mean) - 1 - tf.log(eps + tf.square(hidden3_sigma))) latent_loss = 0.5 * tf.reduce_sum( tf.exp(hidden3_gamma) + tf.square(hidden3_mean) - 1 - hidden3_gamma) n_inputs = 28 * 28 # for MNIST n_hidden1 = 500 n_hidden2 = 500 n_hidden3 = 20 # codings n_hidden4 = n_hidden2 n_hidden5 = n_hidden1 n_outputs = n_inputs learning_rate = 0.001 with tf.contrib.framework.arg_scope( [fully_connected], activation_fn=tf.nn.elu, weights_initializer=tf.contrib.layers.variance_scaling_initializer()): X = tf.placeholder(tf.float32, [None, n_inputs]) hidden1 = fully_connected(X, n_hidden1) hidden2 = fully_connected(hidden1, n_hidden2) # 中间层是一个分布的表示,并加入一个noise hidden3_mean = fully_connected(hidden2, n_hidden3, activation_fn=None) hidden3_gamma = fully_connected(hidden2, n_hidden3, activation_fn=None) hidden3_sigma = tf.exp(0.5 * hidden3_gamma) noise = tf.random_normal(tf.shape(hidden3_sigma), dtype=tf.float32) # 使用带noise的层来键之后的层 hidden3 = hidden3_mean + hidden3_sigma * noise hidden4 = fully_connected(hidden3, n_hidden4) hidden5 = fully_connected(hidden4, n_hidden5) logits = fully_connected(hidden5, n_outputs, activation_fn=None) outputs = tf.sigmoid(logits) reconstruction_loss = tf.reduce_sum( tf.nn.sigmoid_cross_entropy_with_logits(labels=X, logits=logits)) latent_loss = 0.5 * tf.reduce_sum( tf.exp(hidden3_gamma) + tf.square(hidden3_mean) - 1 – hidden3_gamma) cost = reconstruction_loss + latent_loss optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(cost) init = tf.global_variables_initializer() # 生成数据 import numpy as np n_digits = 60 n_epochs = 50 batch_size = 150 with tf.Session() as sess: init.run() for epoch in range(n_epochs): n_batches = mnist.train.num_examples // batch_size for iteration in range(n_batches): X_batch, y_batch = mnist.train.next_batch(batch_size) sess.run(training_op, feed_dict={X: X_batch}) codings_rnd = np.random.normal(size=[n_digits, n_hidden3]) outputs_val = outputs.eval(feed_dict={hidden3: codings_rnd}) for iteration in range(n_digits): plt.subplot(n_digits, 10, iteration + 1) plot_image(outputs_val[iteration])
生成结果如下所示,都是训练集中没有出现的图像
