[CF788B Weird journey] 星际旅行（欧拉路）

CF788B [Weird Jouney]

原题目地址

一句话题意：总共有(n)个节点，(m)条路径，要求其中(m-2)条路径走两遍，剩下(2)条路径仅走一遍，问不同的路径总数有多少，如果仅走一遍的两条边不同则将这两条路径视为不同。

Solution

直接把边拆成两条，显然这样每个点的度数都是偶数
整个图构成欧拉路
题目意思就是说删去两条边之后仍然构成欧拉路
那么根据欧拉路的性质可以知道
删去的两条边必连在同一个点上
这样保证了有两个点的度数变成奇数的情况下
和他们连的那个点度数-2，仍然为偶数
整张图依然是欧拉路

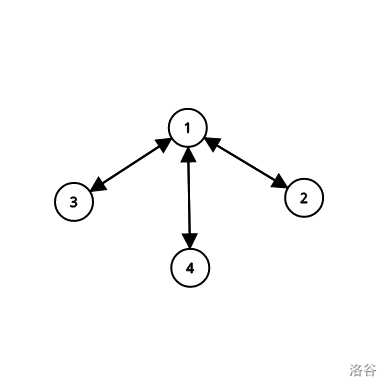
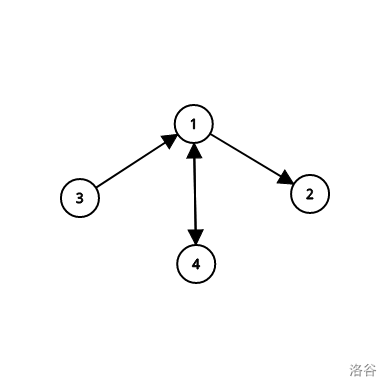
下面考虑对答案有贡献的三种情况((circle为自环数量))

• 两个自环对答案做贡献，总贡献(frac {circle * (circle - 1) } 2)建议手模
• 一个自环一条边，贡献值((circle) * (m - circle))
• 两条边(frac {(du[i] * (du[i] - 1)} 2)

注意

• 统计答案开(long : long)，最后一种两条边的情况也要开
• 判断整张图是否连通，若不连通输出0，可以选择冰茶几或者dfs，总之随便搞搞都能判

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;

inline int read(){
	int x = 0, w = 1;
	char ch = getchar();
	for(; ch > '9' || ch < '0'; ch = getchar()) if(ch == '-') w = -1;
	for(; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
	return x * w;
}

const int ss = 2000010;

int fa[ss], du[ss];

inline int find(int u){
	if(u == fa[u]) return u;
	return fa[u] = find(fa[u]);
}

inline void link(int u, int v){
	int xx = find(u), yy = find(v);
	if(xx != yy) fa[xx] = yy;
}

long long ans;
int l[ss], r[ss];
int circle;

signed main(){
	int n = read(), m = read();
	for(int i = 1; i <= n; i++) fa[i] = i;
	for(int i = 1; i <= m; i++){
		l[i] = read(), r[i] = read();
		link(l[i], r[i]);
		if(l[i] == r[i]) circle++;
		else{
			du[l[i]]++;
			du[r[i]]++;
		}
	}
	int begin = find(l[1]);
	for(int i = 2; i <= m; i++)
		if(find(l[i]) != begin)
			return puts("0"), 0;
	ans += (circle - 1) * circle / 2;
	ans += (circle) * (m - circle);
	for(int i = 1; i <= n; i++)
		ans += (long long)du[i] * (du[i] - 1) / 2;
	printf("%lld
", ans);
	return 0;
}