C++11 随机数生成器

背景

考试想造浮点数然后发现不会
正好下午被虎哥茶话会
谈到了一些不会的问题balabala的
被告知(C++11)有些神奇特性（哦豁）
然后就学习了一手看上去没什么用的随机数生成器(QwQ)

函数

random_device

标准库提供了一个非确定性随机数生成设备
在(Linux)的实现中,是读取(/dev/urandom)设备
random_device提供()操作符,用来返回一个min()到max()之间的一个数字
如果是(Linux(Unix Like或者Unix))下,都可以使用这个来产生高质量的随机数,可以理解为真随机数
（以上都是废话，其实和最原始的c++的rand()用法一样，不过真随机数好评）

#include <iostream>
#include <random>
using namespace std;
signed main(){
	random_device rand;
   	cout << rand() << endl;
        return 0;
}

default_random_engine

一个随机化的前置引擎
给后面要用到的函数生成一个随机节点（时间戳balabala随便理解一下就好，并没有什么卵用，就是让后面的函数随机化更强）
和上面提到的random_device不同的是，这个需要提供时间种子，看上去和rand也没什么区别。。。

#include <iostream>
#include <random>
using namespace std;
signed main(){
	default_random_engine rand(time(NULL));
   	cout << rand() << endl;
	return 0;
}

uniform_int_distribution

好了干货来了
该函数的作用是生成一个[a,b]范围内的整数
定义的时候传进去相应的参数（数据范围即可）

uniform_int_distribution<int> rand1(-100, 100);

调用的时候给时间种子（就是上面device写的rand函数）

cout << rand1(rand) << " ";

uniform_real_distribution

最有用的东西还是这个实数域的随机生成器
用法和上述int一样

uniform_real_distribution<double> rand2(0.0, 1.0);
cout << rand2(rand) << endl;

正态分布normal_distribution

再来说一个常用的
正态分布
正态分布(N(μ,σ^2))呈现经典的”钟形曲线”的形状，其中中心峰的(x)坐标由(μ)给出，峰的宽度受(σ)控制。
正态分布由两个参数控制，(μ∈R)和(σ∈(0,∞))
分布的标准差用(σ)表示，方差用(σ^2)表示
使用方法，第一个参数是(μ)，第二个是(σ)

normal_distribution<double> N(10.0, 5.0);

为了方便直观的看出数据分布，把每次生成的数据出现次数+1，测试的时候输出了数据分布图像

for(register int i = 0; i < 10000; i++){
	      double num = nor(rand);
	      if ((num >= 0.0) && (num < 20.0)) ++p[int(num)];
	}
	for (int i = 0; i < 20; ++i) {
    	cout << i << "-" << (i + 1) << ": ";
    	cout << string(p[i] * 100 / 10000, '*') << endl;
}

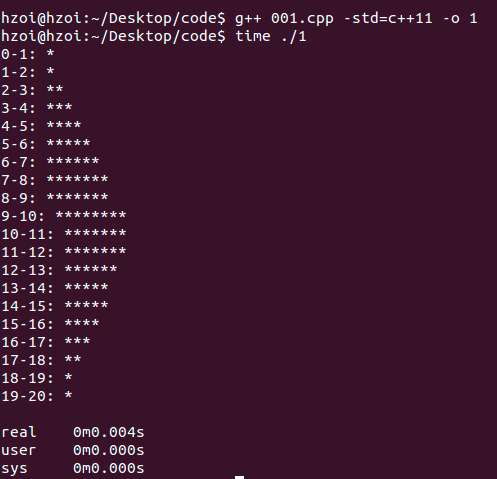
具体要求按照具体题目要求，修改参数即可

Code

最后把代码粘贴一下，有需要自取就好

#include <iostream>
#include <random>
using namespace std;

int p[1000];

signed main(){
	default_random_engine rand(time(NULL));
	
	uniform_int_distribution<int> rand1(-100, 100);
	uniform_real_distribution<double> rand2(0.0, 1.0);
	cout << rand() << " ";
	cout << rand1(rand) << " ";
	cout << rand2(rand) << endl;
	
	normal_distribution<double> nor(10.0, 5.0);
	for(register int i = 0; i < 10000; i++){
		double num = nor(rand);
		if ((num >= 0.0) && (num < 20.0)) ++p[int(num)];
	}
	for (int i = 0; i < 20; ++i) {
    	cout << i << "-" << (i + 1) << ": ";
    	cout << std::string(p[i] * 100 / 10000, '*') << std::endl;
	}
	return 0;
}

小结

目前常用的这些
如果后续再有需求再补充吧
哦对了
因为是C++11特性
编译命令

g++ 001.cpp -std=c++11 -o 1