广度优先遍历是最简单的图搜索算法之一,也是许多重要的图算法的模型。
图的表示
对于图G=(V,E)(V代表图中结点的集合,E代表图中所有边的集合),可以用两种标准表示方法表示:
1.将图作为邻接链表的组合
对于图G=(V,E),其邻接链表表示由一个包含|V|条链表的数组Adj构成。
对于每个结点u∈V,邻接链表Adj[u]包含图G中所有与u邻接的结点
2.将图作为邻接矩阵来看待
对于邻接矩阵表示来说,我们将图G的结点编号为1,2,...,|V|,用一个|V|×|V|的矩阵来表示图G,该矩阵满足下述条件:
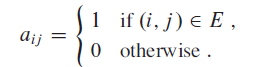
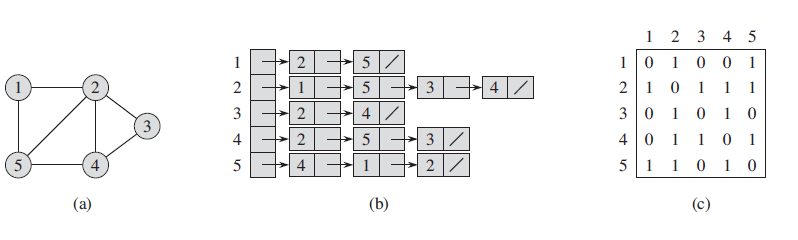
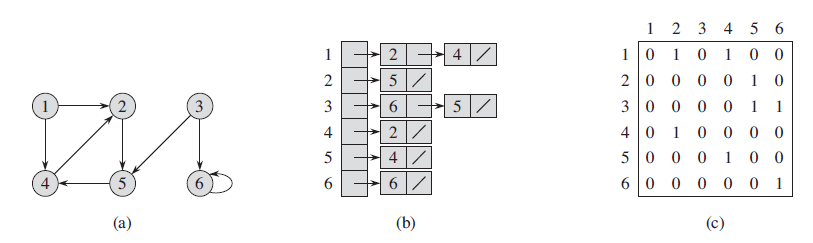
下面分别展示了有向图跟无向图的两种表示方法
广度优先遍历
广度优先遍历的基本思想如下:
1、从图中某个顶点V0出发,并访问此顶点;
2、从V0出发,访问V0的各个未曾访问的邻接点W1,W2,…,Wk;然后,依次从W1,W2,…,Wk出发访问各自未被访问的邻接点;
3、重复步骤2,直到全部顶点都被访问为止。
首先我们把图中的每个结点都涂成白色。在算法推进过程中,当第一次遇到该结点时,其颜色会发生改变而且符合下面条件:
所有与黑色结点邻接的结点都已经被发现,而对于灰色结点来说,其邻接结点中可能存在未被发现的白色结点。
假定输入图G=(V,E)是以邻接链表锁表示的,下面给出了广度优先搜索过程BFS的伪代码
1 BFS(G,s) 2 for each vertex u∈G.V-{s} 3 u.color=WHITE 4 u.d=∞ 5 u.π=NIL 6 s.color=GRAY 7 s.d=0 8 s.π=NIL 9 Q=∅ 10 ENQUEUE(Q,s) 11 while Q≠∅ 12 u=DEQUEUE(Q) 13 for each v∈G.Adj[u] 14 if v.color=WHITE 15 v.color=GRAY 16 v.d=u.d+1 17 v.π=u 18 ENQUEUE(Q,v) 19 u.color=BLACK
其中每个加点的颜色存放在属性u.color中,u的前驱结点存放在属性u.π中,属性u.d记录从源结点s到结点u之间的距离,用一个先进先出的队列Q来管理灰色结点集。
下图描述的是BFS在一个样本图中的推进过程
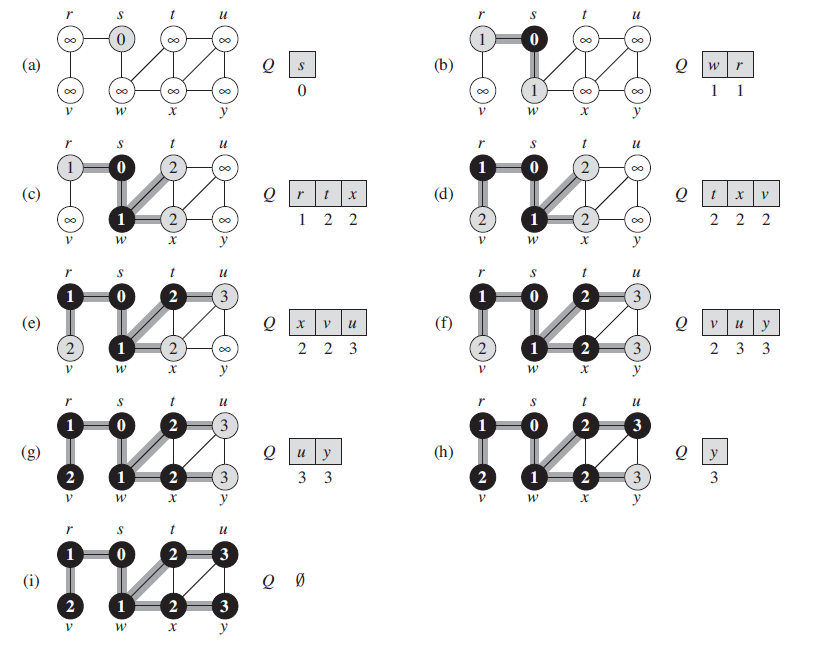
把结点涂成灰色是为了方便查看推进的顺序,实际算法中只需要涂成白色或者黑色。