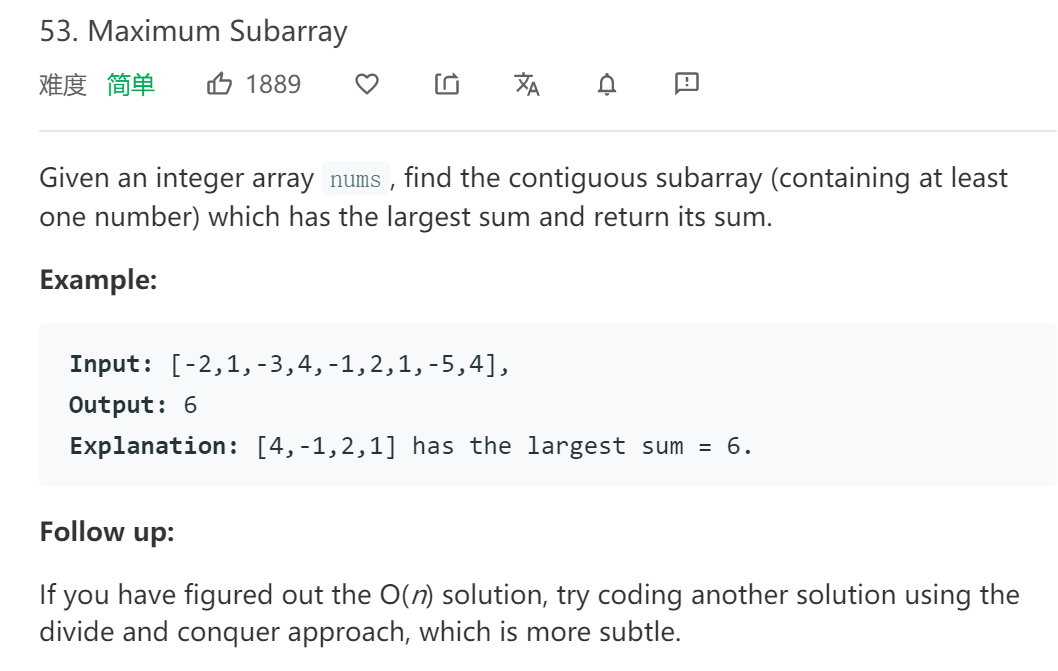
这类题目的往往可以采用暴力穷举的办法,但其时间复杂度过高。因此,这里采用动态规划的方法求解。设定一个状态集合dp[numsSize]与nums[numsSize]一一对应,对dp[0]初始化为nums[0],之后的每一个状态都赋值为max{nums[i], nums[i]+dp[i-1]},这里的意思就是每往后扫描一个元素,返回该元素或该元素和前一状态的和,也就是说只有该元素为正值,才会引起dp的增加,否则dp与nums保持一致,抛弃之前求和很小的状态。因为这里我设了一个dp数组,因此空间复杂度为O(n),当然由于每次dp值的更新只需要其前一个值,最后结果并不需要回头查询每个状态,因此可以优化为O(1)的空间复杂度。对于时间复杂度,从循环来看,只需要对数组中的元素遍历一次,时间复杂度为O(n).
我的题解代码如下,leetcode上运行时间4ms,内存占用6MB
#define MIN_NUM -9999 int maxSubArray(int *nums,int numsSize){ int maxSum=MIN_NUM; int *dp=(int *)malloc(sizeof(int)*numsSize); dp[0]=nums[0]; maxSum=dp[0]; for(int i=1;i<numsSize;i++){ dp[i]=(dp[i-1]+nums[i])>nums[i]?(dp[i-1]+nums[i]):nums[i]; maxSum=dp[i]>maxSum?dp[i]:maxSum; } return maxSum; }