LM拟合算法

一、  Levenberg-Marquardt算法

（1）y=a*e.^(-b*x)形式拟合

clear all
% 计算函数f的雅克比矩阵，是解析式
syms a b y x real;
f=a*exp(-b*x);
Jsym=jacobian(f,[a b]);
% 拟合用数据。参见《数学试验》，p190，例2
% data_1=[0.25 0.5 1 1.5 2 3 4 6 8];
% obs_1=[19.21 18.15 15.36 18.10 12.89 9.32 7.45 5.24 3.01];
load fla
% data_1=[0.25 0.5 1 1.5 2 3 4 6 8];
% obs_1=[19.21 18.15 15.36 18.10 12.89 9.32 7.45 5.24 3.01];
data_1=1:26;
obs_1=fla3_1;%y轴的值

% 2. LM算法
% 初始猜测s
a0=1e+09; b0=0;
y_init = a0*exp(-b0*data_1);
% 数据个数
Ndata=length(obs_1);
% 参数维数
Nparams=2;
% 迭代最大次数
n_iters=50;
% LM算法的阻尼系数初值
lamda=0.01;
% step1: 变量赋值
updateJ=1;
a_est=a0;
b_est=b0;
%% 
% step2: 迭代
for it=1:n_iters %迭代次数
   if updateJ==1
       % 根据当前估计值，计算雅克比矩阵
       J=zeros(Ndata,Nparams);%数据的维度，系数的维度
       for i=1:length(data_1)
           J(i,:)=[exp(-b_est*data_1(i)) -a_est*data_1(i)*exp(-b_est*data_1(i))];%雅克比矩阵的生成
                                                                                 % 对系数a和b求导
       end
       % 根据当前参数，得到函数值
       y_est = a_est*exp(-b_est*data_1);
       % 计算误差
       d=obs_1-y_est;
       % 计算（拟）海塞矩阵
       H=J'*J;
       % 若是第一次迭代，计算误差
       if it==1
           e=dot(d,d);%向量点乘
       end
   end
   % 根据阻尼系数lamda混合得到H矩阵
   H_lm=H+(lamda*eye(Nparams,Nparams)); % J'*J+lamda*I
   % 计算步长dp，并根据步长计算新的可能的参数估计值
   dp=inv(H_lm)*(J'*d(:)); %deltp=[J'*J+lamda*I]^(-1)*(J'*εk)矩阵求逆
   g = J'*d(:);
   a_lm=a_est+dp(1);
   b_lm=b_est+dp(2);
   % 计算新的可能估计值对应的y和计算残差e
   y_est_lm = a_lm*exp(-b_lm*data_1);
   d_lm=obs_1-y_est_lm;
   e_lm=dot(d_lm,d_lm);
   % 根据误差，决定如何更新参数和阻尼系数
   if e_lm<e
       lamda=lamda/10;
       a_est=a_lm;
       b_est=b_lm;
       e=e_lm;
       disp(e);
       updateJ=1;
   else
       updateJ=0;
       lamda=lamda*10;
   end
end
%% 
%显示优化的结果
a_est
b_est
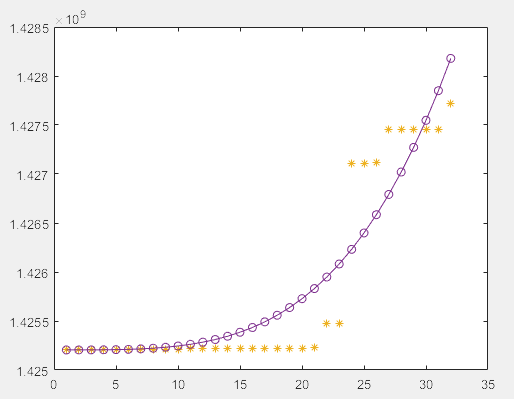
%从图形上观察拟合程度
plot(data_1,obs_1,'*')
hold on
x=1:54;
y=a_est*exp(-b_est*x);
plot(x,y,'o-')

（2）y=a*x.^b+c形式

注意公式变化后，求导的变化 

clear all
% 计算函数f的雅克比矩阵，是解析式
syms a b c x ;
f=a*x.^b+c;
Jsym=jacobian(f,[a b c]);
% 拟合用数据。参见《数学试验》，p190，例2
% data_1=[0.25 0.5 1 1.5 2 3 4 6 8];
% obs_1=[19.21 18.15 15.36 18.10 12.89 9.32 7.45 5.24 3.01];
load fla
% data_1=[0.25 0.5 1 1.5 2 3 4 6 8];
% obs_1=[19.21 18.15 15.36 18.10 12.89 9.32 7.45 5.24 3.01];
data_1=1:length(fla3_1);
obs_1=fla3_1;%y轴的值

% 2. LM算法
% 初始猜测s
a0=1e+09; b0=0;c0=1.4e+09;
y_init = a0*data_1.^b0+c0;
% 数据个数
Ndata=length(obs_1);
% 参数维数
Nparams=3;
% 迭代最大次数
n_iters=50;
% LM算法的阻尼系数初值
lamda=0.01;
% step1: 变量赋值
updateJ=1;
a_est=a0;
b_est=b0;
c_est=c0;
%% 
% step2: 迭代
for it=1:n_iters %迭代次数
   if updateJ==1
       % 根据当前估计值，计算雅克比矩阵
       J=zeros(Ndata,Nparams);%数据的维度，系数的维度
       for i=1:length(data_1)
           J(i,:)=[data_1(i).^b_est a_est*log(data_1(i))*data_1(i).^b_est 0];%雅克比矩阵的生成
                                                                                 % 对系数a和b求导
       end
       % 根据当前参数，得到函数值
       y_est =a_est*data_1.^b_est+c_est ;
       % 计算误差
       d=obs_1-y_est;
       % 计算（拟）海塞矩阵
       H=J'*J;
       % 若是第一次迭代，计算误差
       if it==1
           e=dot(d,d);%向量点乘
       end
   end
   % 根据阻尼系数lamda混合得到H矩阵
   H_lm=H+(lamda*eye(Nparams,Nparams)); % J'*J+lamda*I
   % 计算步长dp，并根据步长计算新的可能的参数估计值
   dp=inv(H_lm)*(J'*d(:)); %deltp=[J'*J+lamda*I]^(-1)*(J'*εk)矩阵求逆
   g = J'*d(:);
   a_lm=a_est+dp(1);
   b_lm=b_est+dp(2);
   c_lm=c_est+dp(3);
   % 计算新的可能估计值对应的y和计算残差e
   y_est_lm = a_lm*data_1.^b_lm+c_lm;
   d_lm=obs_1-y_est_lm;
   e_lm=dot(d_lm,d_lm);
   % 根据误差，决定如何更新参数和阻尼系数
   if e_lm<e
       lamda=lamda/10;
       a_est=a_lm;
       b_est=b_lm;
       e=e_lm;
       disp(e);
       updateJ=1;
   else
       updateJ=0;
       lamda=lamda*10;
   end
end
%% 
%显示优化的结果
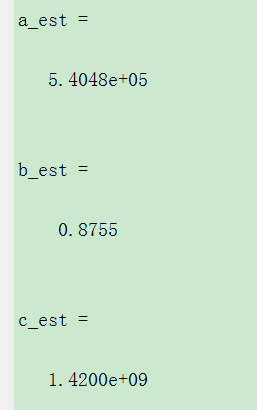
a_est
b_est
c_est
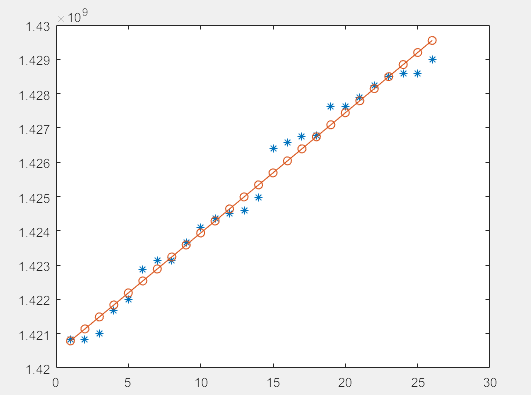
%从图形上观察拟合程度
plot(data_1,obs_1,'*')
hold on
x=1:length(data_1);
y=a_est*data_1.^b_est+c_est;
plot(x,y,'o-')

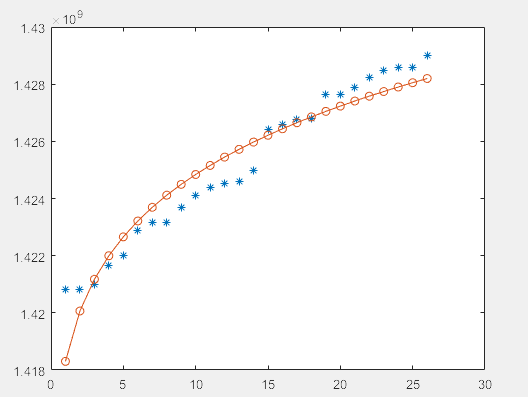
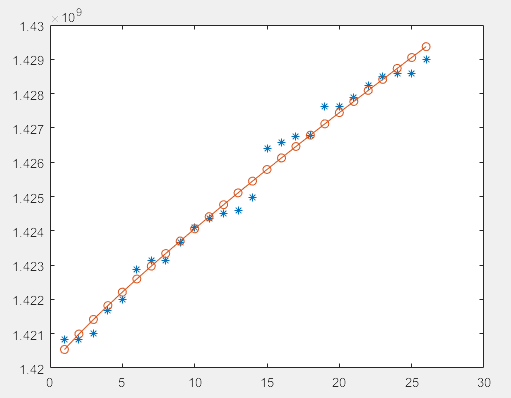
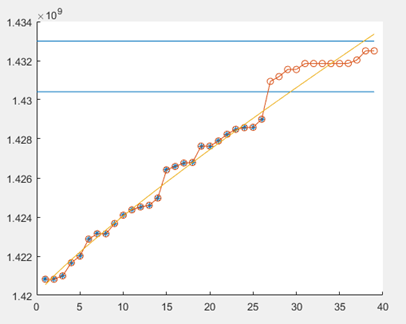
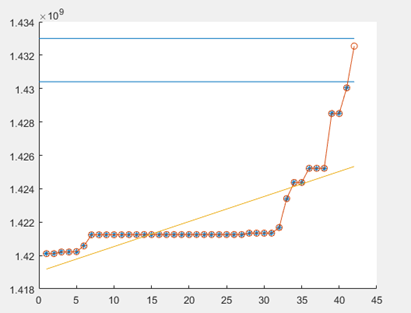
拟合不是很好

更改初始参数c0=1.42e+09后，变为如下图，拟合效果好很多，所以参数调整很重要。

LM函数

function [a_est,b_est,c_est]=LM(data)
    data_1=1:length(data);
    obs_1=data;%y轴的值

    % 2. LM算法
    % 初始猜测s
    a0=1; b0=0;c0=1.42e+09;
    y_init = a0*data_1.^b0+c0;
    % 数据个数
    Ndata=length(obs_1);
    % 参数维数
    Nparams=3;
    % 迭代最大次数
    n_iters=500;
    % LM算法的阻尼系数初值
    lamda=0.01;
    % step1: 变量赋值
    updateJ=1;
    a_est=a0;
    b_est=b0;
    c_est=c0;
    %% 
    % step2: 迭代
    for it=1:n_iters %迭代次数
       if updateJ==1
           % 根据当前估计值，计算雅克比矩阵
           J=zeros(Ndata,Nparams);%数据的维度，系数的维度
           for i=1:length(data_1)
               J(i,:)=[data_1(i).^b_est a_est*log(data_1(i))*data_1(i).^b_est 0];%雅克比矩阵的生成
                                                                                     % 对系数a和b求导
           end
           % 根据当前参数，得到函数值
           y_est =a_est*data_1.^b_est+c_est ;
           % 计算误差
           d=obs_1-y_est;
           % 计算（拟）海塞矩阵
           H=J'*J;
           % 若是第一次迭代，计算误差
           if it==1
               e=dot(d,d);%向量点乘
           end
       end
       % 根据阻尼系数lamda混合得到H矩阵
       H_lm=H+(lamda*eye(Nparams,Nparams)); % J'*J+lamda*I
       % 计算步长dp，并根据步长计算新的可能的参数估计值
       dp=inv(H_lm)*(J'*d(:)); %deltp=[J'*J+lamda*I]^(-1)*(J'*εk)矩阵求逆
       g = J'*d(:);
       a_lm=a_est+dp(1);
       b_lm=b_est+dp(2);
       c_lm=c_est+dp(3);
       % 计算新的可能估计值对应的y和计算残差e
       y_est_lm = a_lm*data_1.^b_lm+c_lm;
       d_lm=obs_1-y_est_lm;
       e_lm=dot(d_lm,d_lm);
       % 根据误差，决定如何更新参数和阻尼系数
       if e_lm<e
           lamda=lamda/10;
           a_est=a_lm;
           b_est=b_lm;
           e=e_lm;
           disp(e);
           updateJ=1;
       else
           updateJ=0;
           lamda=lamda*10;
       end
    end

　

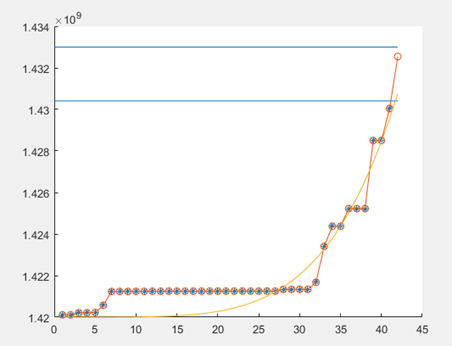
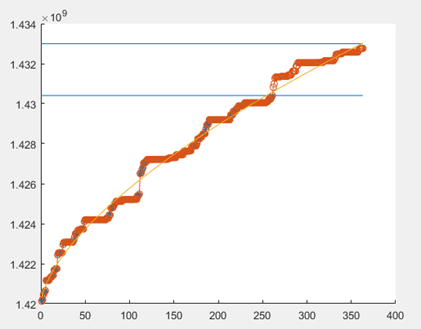
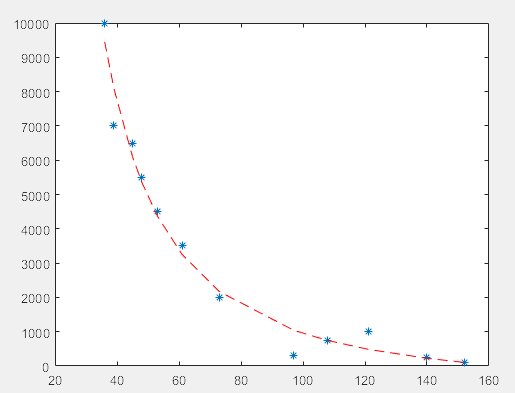
 二、nlinfit拟合

clear;clc
x=[36 39 45 48 53 61 73 97 108 121 140 152];
y=[10000 7000 6500 5500 4500 3500 2000 300 750 1000 250 100];
a0=[0 0 0];
a=nlinfit(x,y,'gx',a0);
s=30:0.01:160;
plot(x,y,'*',x,gx(a,x),'--r')
a=vpa(a,5)

function q=gx(a,x)
q=a(1)*x.^a(2)+a(3);
end

　

 三、最小二乘法

%最小二乘法
function [a,b]=Least_sqr(data)%%
    x=1:length(data);
    y=data;
    s_xy=sum(x.*y);
    s_xx=sum(x.*x);
    s_sxy=sum(x)*sum(y)/length(x);
    s_sx=sum(x).*sum(x)/length(x);
    ave_x=sum(x)/length(x);
    ave_y=sum(y)/length(y);
    a=(s_xy-s_sxy)/(s_xx-s_sx);
    b=ave_y-a*ave_x;
end

　

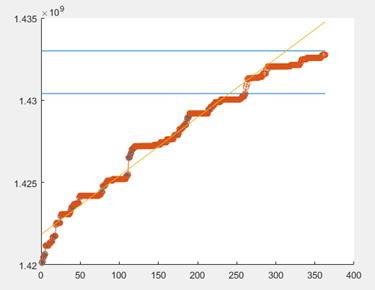
 四、对LM算法的介绍

LM算法的实现并不算难，它的关键是用模型函数 f 对待估参数向量p在其邻域内做线性近似，忽略掉二阶以上的导数项，从而转化为线性最小二乘问题，它具有收敛速度快等优点。LM算法属于一种“信赖域法”——所谓的信赖域法，此处稍微解释一下：在最优化算法中，都是要求一个函数的极小值，每一步迭代中，都要求目标函数值是下降的，而信赖域法，顾名思义，就是从初始点开始，先假设一个可以信赖的最大位移s，然后在以当前点为中心，以s为半径的区域内，通过寻找目标函数的一个近似函数（二次的）的最优点，来求解得到真正的位移。在得到了位移之后，再计算目标函数值，如果其使目标函数值的下降满足了一定条件，那么就说明这个位移是可靠的，则继续按此规则迭代计算下去；如果其不能使目标函数值的下降满足一定的条件，则应减小信赖域的范围，再重新求解。

事实上，你从所有可以找到的资料里看到的LM算法的说明，都可以找到类似于“如果目标函数值增大，则调整某系数再继续求解；如果目标函数值减小，则调整某系数再继续求解”的迭代过程，这种过程与上面所说的信赖域法是非常相似的，所以说LM算法是一种信赖域法。

 

LM算法需要对每一个待估参数求偏导，所以，如果你的目标函数f非常复杂，或者待估参数相当地多，那么可能不适合使用LM算法，而可以选择Powell算法——Powell算法不需要求导。

 

至于这个求导过程是如何实现的，我还不能给出建议，我使用过的方法是拿到函数的方程，然后手工计算出其偏导数方程，进而在函数中直接使用，这样做是最直接，求导误差也最小的方式。不过，在你不知道函数的形式之前，你当然就不能这样做了——例如，你提供给了用户在界面上输入数学函数式的机会，然后在程序中解析其输入的函数，再做后面的处理。在这种情况下，我猜是需要使用数值求导算法的，但我没有亲自试验过这样做的效率，因为一些优秀的求导算法——例如Ridders算法——在一次求导数值过程中，需要计算的函数值次数也会达到5次以上。这样的话，它当然要比手工求出导函数（只需计算一次，就可以得到导数值）效率要差得多了。不过，我个人估计（没有任何依据的，只是猜的）：依赖于LM算法的高效，就算添加了一个数值求导的“拖油瓶”，整个最优化过程下来，它仍然会优于Powell等方法。

关于偏导数的求取

个人认为：在条件允许、对速度和精度任何以方面都有一定要求的前提下，如果待求解的函数形式是显式的，应当尽量自己计算目标函数的偏导数方程。原因在于，在使用数值法估计偏导数值时，尽管我们可以控制每一步偏导数值的精度，但是由于求解过程需要进行多次迭代，特别是收敛过程比较慢的求解过程，需要进行很多次的求解，每一次求解的误差偏差都会在上一步偏差的基础上不断累积。尽管在最后依然可以收敛，但是得到的解已经离可以接受的解偏离比较远了。因此，在求解函数形式比较简单、偏导数函数比较容易求取时，还是尽量手动计算偏导数，得到的结果误差相对更小一些。

 

在这篇解释信赖域算法的文章中，我们已经知道了LM算法的数学模型：

可以证明，此模型可以通过解方程组(Gk+μI)s=−gk确定sk来表征。
即：LM算法要确定一个μ≥0，使得Gk+μI正定，并解线性方程组(Gk+μI)sk=−gk求出sk。
下面来看看LM算法的基本步骤：

·从初始点x0，μ0>0开始迭代

·到第k步时，计算xk和μk

·分解矩阵Gk+μkI，若不正定，令μk=4μk并重复到正定为止

·解线性方程组(Gk+μkI)sk=−gk求出sk并计算rk

·若rk<0.25，令μk+1=4μk；若rk>0.75，令μk+1=μk2；若0.25≤rk≤0.75，令μk+1=μk

·若rk≤0，说明函数值是向着上升而非下降的趋势变化了（与最优化的目标相反），这说明这一步走错了，而且错得“离谱”，此时，不应该走到下一点，而应“原地踏步”，即xk+1=xk，并且和上面rk<0.25的情况一样对μk进行处理。反之，在rk>0的情况下，都可以走到下一点，即xk+1=xk+sk

·        迭代的终止条件：∥gk∥<ε，其中ε是一个指定的小正数（大家可以想像一下二维平面上的寻优过程（函数图像类似于抛物线），当接近极小值点时，迭代点的梯度趋于0）

从上面的步骤可见，LM求解过程中需要用到求解线性方程组的算法，一般我们使用高斯约当消元法，因为它非常稳定——虽然它不是最快最好的算法。
同时，上面的算法步骤也包含对矩阵进行分解的子步骤。为什么要先分解矩阵，再解线性方程组？貌似是这样的（数学不好的人再次泪奔）：不分解矩阵使之正定，就无法确定那个线性方程组是有解的。矩阵分解有很多算法，例如LU分解等，这方面我没有看。

https://www.cnblogs.com/shhu1993/p/4878992.html 

三，程序实现

推导过程的博客 https://www.cnblogs.com/monoSLAM/p/5249339.html

clear all
% 计算函数f的雅克比矩阵，是解析式
syms a b c x ;
f=a*x.^b+c;%函数形式
Jsym=jacobian(f,[a b c]);
data=[1425204748.0, 1425204757.0, 1425204759.0, 1425204766.0,...
       1425204768.0, 1425206629.0, 1425209138.0, 1425209139.0,...
       1425209159.0, 1425209167.0, 1425219290.0, 1425219298.0,...
       1425219307.0, 1425219307.0, 1425219381.0, 1425219382.0,...
       1425219390.0,1425223403.0, 1425223411.0, 1425223420.0,...
       1425225096.0, 1425479571.0, 1425479580.0, 1427109036.0,...
       1427109038.0, 1427115143.0, 1427449736.0, 1427449755.0,...
       1427449763.0, 1427449774.0, 1427449775.0, 1427717884.0];
data_1=1:length(data);
obs_1=data;%y轴的值

% 2. LM算法
% 初始猜测s
a0=1; b0=0;c0=data(1);  %设置初始值
y_init = a0*data_1.^b0+c0;
% 数据个数
Ndata=length(obs_1);
% 参数维数
Nparams=3;
% 迭代最大次数
n_iters=200;
% LM算法的阻尼系数初值
lamda=0.01;
% step1: 变量赋值
updateJ=1
a_est=a0;
b_est=b0;
c_est=c0;
%% 
% step2: 迭代
for it=1:n_iters %迭代次数
    if updateJ==1
       % 根据当前估计值，计算雅克比矩阵
       J=zeros(Ndata,Nparams);%数据的维度，系数的维度
       for i=1:length(data_1)
           J(i,:)=[data_1(i).^b_est a_est*log(data_1(i))*data_1(i).^b_est 0];%雅克比矩阵的生成,32*3矩阵
                                                                                 % 对系数a、b、c求导
       end
       % 根据当前参数，得到函数值
       y_est =a_est*data_1.^b_est+c_est ;%32个预测值
       % 计算误差
       d=obs_1-y_est;
       % 计算（拟）海塞矩阵，是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率，对称矩阵
       H=J'*J;
       % 若是第一次迭代，计算误差
       if it==1
           e=dot(d,d);%向量点乘
       end
    end
    
   % 根据阻尼系数lamda混合得到H矩阵
   H_lm=H+(lamda*eye(Nparams,Nparams)); % J'*J+lamda*I
   % 计算步长dp，并根据步长计算新的可能的参数估计值
   dp=inv(H_lm)*(J'*d'); %deltp=[J'*J+lamda*I]^(-1)*(J'*εk)矩阵求逆
   g = J'*d(:);
   
   a_lm=a_est+dp(1);%新的系数值
   b_lm=b_est+dp(2);
   c_lm=c_est+dp(3);
   
   % 计算新的可能估计值对应的y和计算残差e
   y_est_lm = a_lm*data_1.^b_lm+c_lm;
   d_lm=obs_1-y_est_lm;
   e_lm=dot(d_lm,d_lm);
   
   % 根据误差，决定如何更新参数和阻尼系数
   if e_lm<e  %误差变小
       lamda=lamda/10;
       a_est=a_lm;
       b_est=b_lm;
       c_est=c_lm;
       e=e_lm;
       disp(e);
       updateJ=1;
   else
       updateJ=0;
       lamda=lamda*10;
   end
end
%% 
%显示优化的结果
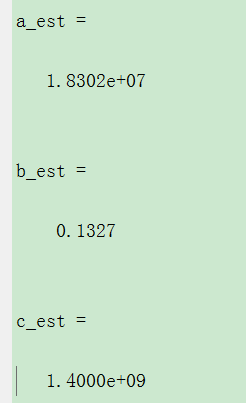
a_est
b_est
c_est
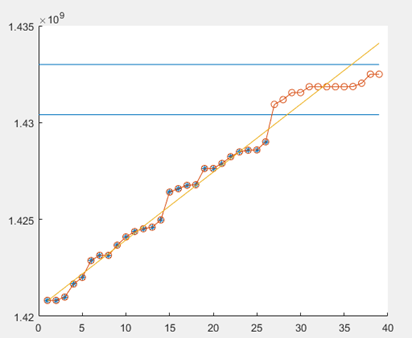
%从图形上观察拟合程度
plot(data_1,obs_1,'*')
hold on
x=1:length(data);
y=a_est*data_1.^b_est+c_est;
plot(x,y,'o-')