Josephu问题

Josephu(约瑟夫)问题

　　约瑟夫问题，有时也称为约瑟夫斯置换，是一个计算机科学和数学中的问题。在计算机编程的算法中，类似问题又称为约瑟夫环。又称“丢手绢问题”。

---

Josephu问题起源

　　据说著名犹太历史学家 Josephus 有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到3的人，该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。

　　然而 Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。问题是，给定了和，一开始要站在什么地方才能避免被处决呢？Josephus 要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

 

　　17世纪的法国数学家加斯帕在《数目的游戏问题》中也讲了这样一个故事：15个教徒和15 个非教徒在深海上遇险，必须将一半的人投入海中，其余的人才能幸免于难，于是想了一个办法：30个人围成一圆圈，从第一个人开始依次报数，每数到九的人，这个人就会被扔入大海，如此循环进行直到仅余15个人为止。问怎样排法，才能使每次投入大海的都是非教徒呢？

 

 

---

Josephu问题描述

丢手绢

　　设编号为1，2，… n的n个人围坐一圈，约定编号为k（1<=k<=n）的人从1开始报数，数到 m 的那个人出列，它的下一位又从1开始报数，数到 m 的那个人又出列，依次类推，直到所有人出列为止，由此产生一个出队编号的序列。

---

算法实现（数据结构）

　　用一个不带头结点的循环链表来处理Josephu 问题：先构成一个有n个结点的单循环链表，然后由k结点起从1开始计数，计到m时，对应结点从链表中删除，然后再从被删除结点的下一个结点又从1开始计数，直到最后一个结点从链表中删除算法结束。

代码实现：

package com.ruoli;

public class Josephu {

    public static void main(String[] args) {
        // 测试一把看看构建环形链表和遍历是否ok
        CircleSingleLinkedList circleSingleLinkedList = new CircleSingleLinkedList();
        circleSingleLinkedList.addBoy(5); // 加入5个小孩节点
        circleSingleLinkedList.show();
        
        // 测试一把小孩出圈是否正确
        circleSingleLinkedList.boyCount(1, 2, 5); // 2->4->1->5->3
    }
}

//小孩结点类
class Boy{
    private int val;
    private Boy next;
    
    public Boy(int val) {
        this.val = val;
    }
    public int getVal() {
        return val;
    }
    public void setVal(int val) {
        this.val = val;
    }
    public Boy getNext() {
        return next;
    }
    public void setNext(Boy next) {
        this.next = next;
    }
}

//环型单链表类（模拟孩子围成的圈）
class CircleSingleLinkedList{
    // 创建一个first节点,当前没有编号
    Boy first = null;
    
    // 添加小孩节点，构建成一个环形的链表
    public void addBoy(int num) {
        if (num < 1) {
            return;
        }
        Boy curBoy = null;
        for (int i = 1; i <= num; i++) {
            Boy boy = new Boy(i);
            if (i == 1) {
                first = boy; // first:第一个结点
                first.setNext(first); // 构成环
                curBoy = first; // 让curBoy指向第一个小孩
            }else {
                curBoy.setNext(boy);
                boy.setNext(first); // 构成环
                curBoy = boy;
            }
        }
    }
    
    // 遍历当前的环形链表
    public void show() {
        // 判断链表是否为空
        if (first == null) {
            System.out.println("此时还没有小孩。。。");
            return;
        }
        // 因为first不能动，因此我们仍然使用一个辅助指针完成遍历
        Boy curBoy = first;
        while (true) {
            System.out.printf("小孩的编号：%d 
", curBoy.getVal());
            if (curBoy.getNext() == first) { // 说明已经遍历完毕
                break;
            }
            curBoy = curBoy.getNext();
        }
    }
    
    // 根据用户的输入，计算出小孩出圈的顺序
    /**
     * 
     * @param startVal：表示从第几个小孩开始数数
     * @param count：表示数几下
     * @param nums：表示最初有多少小孩在圈中
     * @return
     */
    public void boyCount(int start, int count, int nums) {
        // 先对数据进行校验
        if (first == null || start < 1 || start > nums) {
            System.out.println("参数输入有误， 请重新输入");
            return;
        }
        // 创建辅助指针,帮助完成小孩出圈
        Boy helper = first;
        // 创建的辅助指针(变量) helper , 事先应该指向环形链表的最后这个节点
        while (true) {
            if (helper.getNext() == first) {
                break;
            }
            helper = helper.getNext();
        }
        // 小孩报数前，先让 first 和  helper 移动 start - 1次
        for (int i = 0; i < start - 1; i++) {
            first = first.getNext();
            helper = helper.getNext();
        }
        // 当小孩报数时，让first 和 helper 指针同时 的移动  m  - 1 次, 然后出圈
        // 这里是一个循环操作，知道圈中只有一个节点
        while (true) {
            if (helper == first) { // 说明圈中只有一个节点
                break;
            }
            // 让 first 和 helper 指针同时 的移动 count - 1
            for (int i = 0; i < count - 1; i++) {
                first = first.getNext();
                helper = helper.getNext();
            }
            // 这时first指向的节点，就是要出圈的小孩节点
            System.out.printf("小孩%d出圈
", first.getVal());
            // 这时将first指向的小孩节点出圈
            first = first.getNext();
            helper.setNext(first);
        }
        System.out.printf("最后留在圈中的小孩编号%d 
", first.getVal());
    }
}

运行结果：

　　我们所见的面试题，一般会要求我们找到最后一个出队的人，即返回最后一个出队的人的编号。本文只提供一种解决问题的思路和具体的算法实现，如果大家能把上述的算法搞懂，那么在其上稍微修改一下，就能轻松的解决所遇到的面试题了。

参考资料：

　　　　尚硅谷数据结构课程

---

算法实现（数学求解）

　　用链表来模拟小孩子围圈圈，是可以解决问题，但实现起来有点费事，在一些情况下，我们并没有充足的时间来慢慢的实现链表。这时，我们可以用简单一点的方法，这儿只说一种比较好的的方法，还有其他有趣的方法，大家可自行了解。

话不多说，来看求解思路：

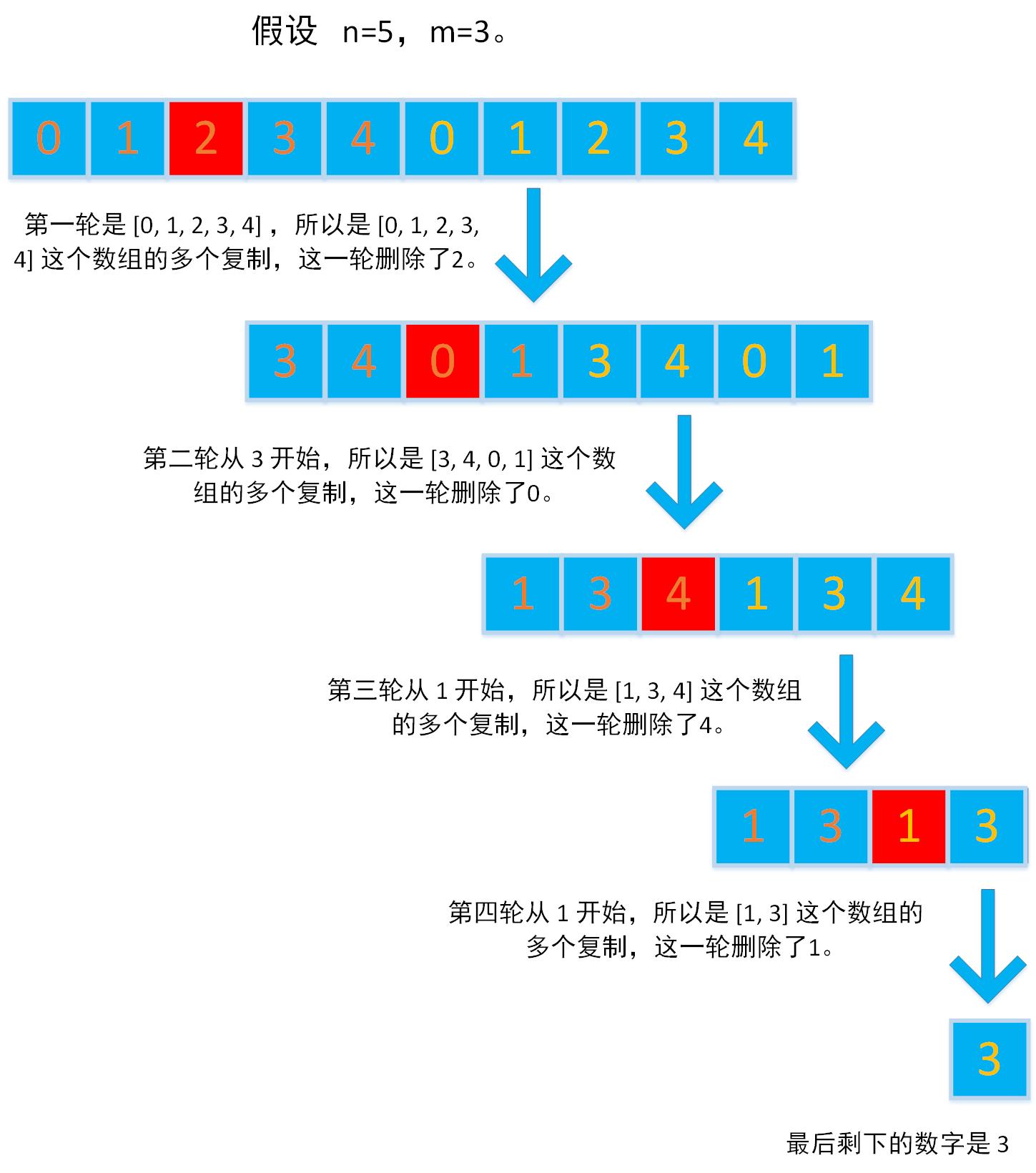
　　我们从最后剩下的 3 倒着看，我们可以反向推出这个数字在之前每个轮次的位置：

　　最后剩下的 3 的下标是 0。

　　第四轮反推，补上 m 个位置，然后模上当时的数组大小 2，位置是(0 + 3) % 2 = 1。

　　第三轮反推，补上 m 个位置，然后模上当时的数组大小 3，位置是(1 + 3) % 3 = 1。

　　第二轮反推，补上 m 个位置，然后模上当时的数组大小 4，位置是(1 + 3) % 4 = 0。

　　第一轮反推，补上 m 个位置，然后模上当时的数组大小 5，位置是(0 + 3) % 5 = 3。

　　所以，最终剩下的数字的下标就是3。因为数组是从0开始的，所以最终的答案就是3。

总结一下：

　　反推的过程就是 (当前index + m) % 上一轮剩余数字的个数。

代码实现：

public class Test {

    public static void main(String[] args) {
        int n = 5;
        int m = 3;
        int result = lastRemaining(n, m);
        System.out.println("最后剩下的人是：" + result + "号");
    }
    
    public static int lastRemaining(int n, int m) {
        int ans = 0;
        // 最后一轮淘汰有2个人，所以从2开始反推
        for (int i = 2; i <= n; i++) {
            ans = (ans + m) % i;
        }
        return ans;
    }
}

运行结果：

　　这种方法要比用链表来模拟效率高的多，但我们刷题的时候，用链表来模拟提交会出现超时，但用这种方法时间复杂度和空间复杂度都小的多，LeetCode提交结果如下：

 参考资料：

　　　　小姐姐的题解。