2583. 南极科考旅行
★★ 输入文件:
BitonicTour.in输出文件:BitonicTour.out简单对比
时间限制:1 s 内存限制:256 MB【题目描述】
小美要在南极进行科考,现在她要规划一下科考的路线。
地图上有 N 个地点,小美要从这 N 个地点中 x 坐标最小的地点 A,走到 x 坐标最大的地点 B,然后再走回地点 A。
请设计路线,使得小美可以考察所有的地点,并且在从 A 到 B 的路程中,考察的地点的 x 坐标总是上升的,在从 B 到 A 的过程中,考察的地点的 x 坐标总是下降的。
求小美所需要走的最短距离(欧几里得距离)。
【输入格式】
输入共 N+1 行。
第 1 行包含 1 个正整数 N,表示地图上共有 N 个地点。
第 1 +(1) 至 1 +(N) 行,每行包含 2 个正整数 x, y,表示其中 1 个地点的坐标。
【输出格式】
输出共 1 行。
第 1 行包含一个浮点数,表示小美需要走的最短距离,保留两位小数。
【样例输入】
4 1 1 2 3 4 1 3 2【样例输出】
8.06【数据范围及约定】
对于前 20% 测试数据
3 <= N <= 6
1 <= x <= 20, 1 <= y <= 20
对于后 80% 测试数据
3 <= N <= 300
1 <= x <= 10000, 1 <= y <= 10000
对于全部测试点,保证每个点坐标的 x 值互不相同
【来源】
Bitonic Tour
题解
乍一看好像一脸 $DP$ 的样子...这种要走一个来回的情形似乎是之前的某个叫做小烈上菜的题...
然而居然出现在了网络流专题里...
行吧网络流就网络流...一开始感觉不会有费用流就开始构最大流(最小割)的图然而直接 $GG$ ...然后意识到是费用流...
woc我不会打费用流啊QAQ
$dbw$ 强行教学一波 $zkw$ 网络流...打完板子开始构图w
首先肯定是要按横坐标排序, 然后我们发现一去一回的方向并没有什么卵用, 找到一个环和找到两条路径是等价的. 这样我们可以发现, 每个结点都必须选择两条边, 其中 $x$ 最小的结点两条都是出边, 最大的结点两条都是入边, 其他结点一条入边一条出边, 这样的话我们可以得到这样的构图:
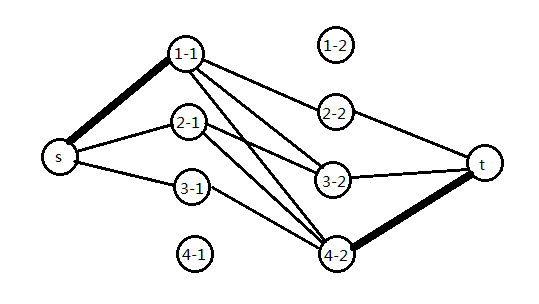
其中较粗的边容量为2, 较细的边容量为1, $s$ 连出的边和连向 $t$ 的边费用为 $0$ , 实际结点间边的距离即为欧几里得距离.
写 $zkw$ 网络流的话有一个坑点: 由于增广时要判断某条边是否在最短路上, 但是现在费用是一个实数, 所以会有精度问题, 直接使用 dis[s]+i->dis==dis[i->to] 判定的话会炸精度死循环, 这点需要注意OwO
参考代码

1 #include <bits/stdc++.h> 2 3 const int MAXV=1e3+10; 4 const int MAXE=2e5+10; 5 const double INF=1e10; 6 const int INFI=0x3F3F3F3F; 7 const double EPSILON=1e-5; 8 9 struct Edge{ 10 int from; 11 int to; 12 int flow; 13 double dis; 14 Edge* rev; 15 Edge* next; 16 }; 17 Edge E[MAXE]; 18 Edge* head[MAXV]; 19 Edge* top=E; 20 21 struct Node{ 22 double x; 23 double y; 24 bool friend operator<(const Node& a,const Node& b){ 25 return a.x<b.x; 26 } 27 }; 28 Node N[MAXV]; 29 30 int n; 31 int v; 32 bool vis[MAXV]; 33 double dis[MAXV]; 34 35 double Sqr(double); 36 bool SPFA(int,int); 37 int DFS(int,int,int); 38 double Dinic(int,int); 39 void Insert(int,int,double,int); 40 double EucDis(const Node&,const Node&); 41 42 int main(){ 43 #ifndef ASC_LOCAL 44 freopen("BitonicTour.in","r",stdin); 45 freopen("BitonicTour.out","w",stdout); 46 #endif 47 scanf("%d",&n); 48 for(int i=1;i<=n;i++){ 49 scanf("%lf%lf",&N[i].x,&N[i].y); 50 } 51 std::sort(N+1,N+1+n); 52 for(int i=2;i<n;i++){ 53 Insert(0,i<<1,0,1); 54 Insert(i<<1|1,1,0,1); 55 } 56 Insert(0,1<<1,0,2); 57 Insert(n<<1|1,1,0,2); 58 v=n*2+2; 59 for(int i=1;i<=n;i++){ 60 for(int j=i+1;j<=n;j++){ 61 Insert(i<<1,j<<1|1,EucDis(N[i],N[j]),1); 62 } 63 } 64 printf("%.2f ",Dinic(0,1)); 65 return 0; 66 } 67 68 double Dinic(int s,int t){ 69 double ans=0; 70 while(SPFA(s,t)){ 71 memset(vis,0,sizeof(vis)); 72 ans+=DFS(s,INFI,t)*dis[t]; 73 } 74 return ans; 75 } 76 77 int DFS(int s,int flow,int t){ 78 if(s==t||flow==0) 79 return flow; 80 int tmp=flow; 81 int k; 82 vis[s]=true; 83 for(Edge* i=head[s];i!=NULL&&tmp>0;i=i->next){ 84 if(i->flow>0&&fabs(dis[i->from]+i->dis-dis[i->to])<EPSILON&&!vis[i->to]){ 85 k=DFS(i->to,std::min(tmp,i->flow),t); 86 tmp-=k; 87 i->flow-=k; 88 i->rev->flow+=k; 89 } 90 } 91 return flow-tmp; 92 } 93 94 bool SPFA(int s,int t){ 95 for(int i=0;i<v;i++) 96 dis[i]=INF; 97 memset(vis,0,sizeof(vis)); 98 std::queue<int> q; 99 q.push(s); 100 vis[s]=true; 101 dis[s]=0; 102 while(!q.empty()){ 103 s=q.front(); 104 vis[s]=false; 105 q.pop(); 106 for(Edge* i=head[s];i!=NULL;i=i->next){ 107 if(i->flow>0&&dis[s]+i->dis<dis[i->to]){ 108 dis[i->to]=dis[s]+i->dis; 109 if(!vis[i->to]){ 110 q.push(i->to); 111 vis[i->to]=true; 112 } 113 } 114 } 115 } 116 return dis[t]<INFI; 117 } 118 119 void Insert(int from,int to,double dis,int flow){ 120 top->from=from; 121 top->to=to; 122 top->dis=dis; 123 top->flow=flow; 124 top->rev=top+1; 125 top->next=head[from]; 126 head[from]=top++; 127 128 top->from=to; 129 top->to=from; 130 top->dis=-dis; 131 top->flow=0; 132 top->rev=top-1; 133 top->next=head[to]; 134 head[to]=top++; 135 } 136 137 inline double EucDis(const Node& a,const Node& b){ 138 return sqrt(Sqr(a.x-b.x)+Sqr(a.y-b.y)); 139 } 140 141 inline double Sqr(double x){ 142 return x*x; 143 }

