Loops are often used in programs that compute numerical results by starting with an approximate answer and iteratively improving it.
For example, one way of computing square roots is Newton’s method. Suppose that you want to know the square root of a. If you start with almost any estimate, x, you can computer a better estimate with the following formula:

For example, if a is 4 and x is 3:

Which is closer to the correct answer. If we repeat the process with the new estimate, it gets even closer:
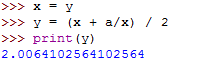
After a few more updates, the estimate is almost the exact:

When y == x, we can stop. Here is a loop that starts with an initial estimate, x, and improves it until it stops changing:

For most values of a this works fine, but in general it is dangerous to test float equality. Floating-point values are only approximately right: most rational numbers, like 1/3 and irrational numbers, like , can’t be represented exactly with a float.
Rather than checking whether x and y are exactly equal, it is safer to use math.fabs to compute the absolute value, or magnitude, of difference between them:
If math.fabs(y-x) < something_small: break
Where something_small has a value like 0.000001 that determines how close is close enough.
Wrap this loop in a function called square_root that takes a as parameter, choose a reasonable value of x, and returns an estimate of the square root of a.

from Thinking in Python