数据结构之哈希（hash）表

最近看PHP数组底层结构，用到了哈希表，所以还是老老实实回去看结构，在这里去总结一下。

1.哈希表的定义

　　这里先说一下哈希（hash）表的定义：哈希表是一种根据关键码去寻找值的数据映射结构，该结构通过把关键码映射的位置去寻找存放值的地方，说起来可能感觉有点复杂，我想我举个例子你就会明白了，最典型的的例子就是字典，大家估计小学的时候也用过不少新华字典吧，如果我想要获取“按”字详细信息，我肯定会去根据拼音an去查找 拼音索引（当然也可以是偏旁索引），我们首先去查an在字典的位置，查了一下得到“安”，结果如下。这过程就是键码映射，在公式里面，就是通过key去查找f(key)。其中，按就是关键字（key），f（）就是字典索引，也就是哈希函数，查到的页码4就是哈希值。

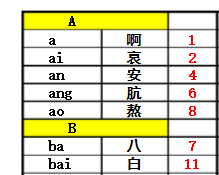
通过字典查询数据

2.哈希冲突

　　但是问题又来了，我们要查的是“按”，而不是“安，但是他们的拼音都是一样的。也就是通过关键字按和关键字安可以映射到一样的字典页码4的位置，这就是哈希冲突（也叫哈希碰撞），在公式上表达就是key1≠key2，但f(key1)=f(key2)。冲突会给查找带来麻烦，你想想，你本来查找的是“按”，但是却找到“安”字，你又得向后翻一两页，在计算机里面也是一样道理的。

　　但哈希冲突是无可避免的，为什么这么说呢，因为你如果要完全避开这种情况，你只能每个字典去新开一个页，然后每个字在索引里面都有对应的页码，这就可以避免冲突。但是会导致空间增大（每个字都有一页）。

　　既然无法避免，就只能尽量减少冲突带来的损失，而一个好的哈希函数需要有以下特点：

　　1.尽量使关键字对应的记录均匀分配在哈希表里面（比如说某厂商卖30栋房子，均匀划分ABC3个区域，如果你划分A区域1个房子，B区域1个房子，C区域28个房子，有人来查找C区域的某个房子最坏的情况就是要找28次）。

　　2.关键字极小的变化可以引起哈希值极大的变化。

　　比较好的哈希函数是time33算法。PHP的数组就是把这个作为哈希函数。

　　核心的算法就是如下：

unsigned long hash(const char* key){
    unsigned long hash=0;
    for(int i=0;i<strlen(key);i++){
        hash = hash*33+str[i];
    }  
    return hash;
}

 3.哈希冲突解决办法

　　 如果遇到冲突，哈希表一般是怎么解决的呢？具体方法有很多，百度也会有一堆，最常用的就是开发定址法和链地址法。

　　1.开发定址法

　　如果遇到冲突的时候怎么办呢？就找hash表剩下空余的空间，找到空余的空间然后插入。就像你去商店买东西，发现东西卖光了，怎么办呢？找下一家有东西卖的商家买呗。

　　由于我没有深入试验过，所以贴上在书上的解释：

 　　2.链地址法

 　　上面所说的开发定址法的原理是遇到冲突的时候查找顺着原来哈希地址查找下一个空闲地址然后插入，但是也有一个问题就是如果空间不足，那他无法处理冲突也无法插入数据，因此需要装填因子(插入数据/空间)<=1。

　　那有没有一种方法可以解决这种问题呢？链地址法可以，链地址法的原理时如果遇到冲突，他就会在原地址新建一个空间，然后以链表结点的形式插入到该空间。我感觉业界上用的最多的就是链地址法。下面从百度上截取来一张图片，可以很清晰明了反应下面的结构。比如说我有一堆数据{1,12,26,337,353...}，而我的哈希算法是H(key)=key mod 16，第一个数据1的哈希值f(1)=1，插入到1结点的后面，第二个数据12的哈希值f(12)=12，插入到12结点，第三个数据26的哈希值f(26)=10，插入到10结点后面，第4个数据337，计算得到哈希值是1，遇到冲突，但是依然只需要找到该1结点的最后链结点插入即可，同理353。

　　

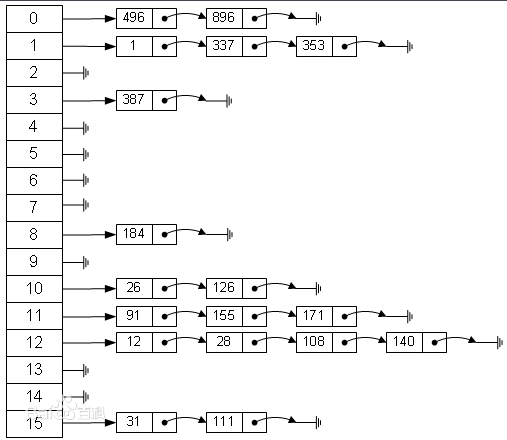
哈希表的拉链法实现

　　下面解析一下如何用C++实现链地址法。

　　第一步。

　　肯定是构建哈希表。

　　首先定义链结点，以结构体Node展示，其中Node有三个属性，一个是key值，一个value值，还有一个是作为链表的指针。还有作为类的哈希表。

#define HASHSIZE 10
typedef unsigned int uint;
typedef struct Node{
    const char* key;
    const char* value;
    Node *next;
}Node;

class HashTable{
private:
    Node* node[HASHSIZE];
public:
    HashTable();
    uint hash(const char* key);
    Node* lookup(const char* key);
    bool install(const char* key,const char* value);
    const char* get(const char* key);
    void display();
};

　　然后定义哈希表的构造方法

HashTable::HashTable(){
    for (int i = 0; i < HASHSIZE; ++i)
    {
        node[i] = NULL;
    }
}

　　第二步。

　　定义哈希表的Hash算法，在这里我使用time33算法。

uint HashTable::hash(const char* key){
    uint hash=0;
    for (; *key; ++key)
    {
        hash=hash*33+*key;
    }
    return hash%HASHSIZE;
}

　　第三步。

　　定义一个查找根据key查找结点的方法，首先是用Hash函数计算头地址，然后根据头地址向下一个个去查找结点，如果结点的key和查找的key值相同，则匹配成功。

Node* HashTable::lookup(const char* key){
    Node *np;
    uint index;
    index = hash(key);
    for(np=node[index];np;np=np->next){
        if(!strcmp(key,np->key))
            return np;
    }
    return NULL;
}

　　第四步。

　　定义一个插入结点的方法，首先是查看该key值的结点是否存在，如果存在则更改value值就好，如果不存在，则插入新结点。

bool HashTable::install(const char* key,const char* value){
    uint index;
    Node *np;
    if(!(np=lookup(key))){
        index = hash(key);
        np = (Node*)malloc(sizeof(Node));
        if(!np) return false;
        np->key=key;
        np->next = node[index];
        node[index] = np;
    }
    np->value=value;
    return true;
}

　　

4.关于哈希表的性能

　　由于哈希表高效的特性，查找或者插入的情况在大多数情况下可以达到O(1)，时间主要花在计算hash上，当然也有最坏的情况就是hash值全都映射到同一个地址上，这样哈希表就会退化成链表，查找的时间复杂度变成O(n)，但是这种情况比较少，只要不要把hash计算的公式外漏出去并且有人故意攻击（用兴趣的人可以搜一下基于哈希冲突的拒绝服务攻击），一般也不会出现这种情况。

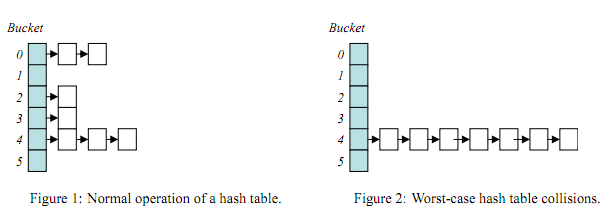
哈希冲突攻击导致退化成链表

　　最后附上完整代码下载地址。点此下载源码