HDU 1024 Max Sum Plus Plus

http://acm.hdu.edu.cn/showproblem.php?pid=1024

题目

Now I think you have got an AC in Ignatius.L's "Max Sum" problem. To be a brave ACMer, we always challenge ourselves to more difficult problems. Now you are faced with a more difficult problem.

Given a consecutive number sequence S ₁, S ₂, S ₃, S ₄ ... S _x, ... S _n (1 ≤ x ≤ n ≤ 1,000,000, -32768 ≤ S _x ≤ 32767). We define a function sum(i, j) = S _i + ... + S _j (1 ≤ i ≤ j ≤ n).

Now given an integer m (m > 0), your task is to find m pairs of i and j which make sum(i ₁, j ₁) + sum(i ₂, j ₂) + sum(i ₃, j ₃) + ... + sum(i _m, j _m) maximal (i _x ≤ i _y ≤ j _x or i _x ≤ j _y ≤ j _x is not allowed).

But I`m lazy, I don't want to write a special-judge module, so you don't have to output m pairs of i and j, just output the maximal summation of sum(i _x, j _x)(1 ≤ x ≤ m) instead. ^_^

题解

不会这种dp，还有这个区间不相交怎么是这样表示的= =

设$dp[i][j]$为前i个数分了j组，且最后一个数在第j组（前面的数字可以不选）

那么易得$dp[i][j]=max left{ dp[i-1][j], dp[i-1][j-1], dp[i-2][j-1], dp[i-3][j-1], cdots , dp[j-1][j-1] ight}+arr[i]$

状态$mathcal{O}(mn)$个，转移$mathcal{O}(n)$个，时间复杂度$mathcal{O}(mn^2)$，远超1e9，显然TLE

只要求求出最大，观察式子，可以发现后面的可以在每次转移的时候求出来

空间问题可以用滚动数组解决（两行），但因为后面的项已经在转移的时候求了，只有一项是重叠的，如图

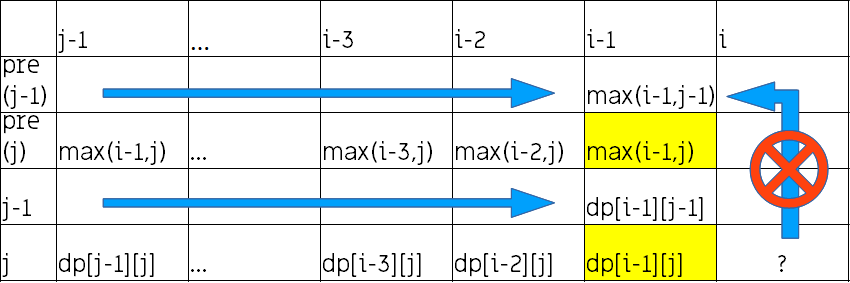
因此我们也可以用一个变量延迟一下= =

AC代码

#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
#include<bits/stdc++.h>
using namespace std;

#define REP(r,x,y) for(register int r=(x); r<(y); r++)
#define PER(r,x,y) for(register int r=(x); r>(y); r--)
#define REPE(r,x,y) for(register int r=(x); r<=(y); r++)
#define PERE(r,x,y) for(register int r=(x); r>=(y); r--)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...) (void)0
#endif

#define MAXN 1000007
template <class T>
inline void read(T& x) {
    char c=getchar();
    int f=1;x=0;
    while(!isdigit(c)&&c!='-')c=getchar();
    if(c=='-')f=-1,c=getchar();
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}x*=f;
}
template <class T,class... A>void read(T&t,A&...a){read(t);read(a...);}

int m,n;
int arr[MAXN];
long long dp[MAXN];
long long pre[MAXN];
int main() {
	#ifdef sahdsg
	freopen("in.txt", "r", stdin);
	#endif
	while(~scanf("%d%d", &m, &n)) {
		
		REPE(i,1,n) {
			read(arr[i]);
		}
		dp[0]=0;
		memset(pre,0,sizeof pre);
		long long tmp=-0x3f3f3f3f;
		REPE(j,1,m) {
			tmp=-0x3f3f3f3f;
			REPE(i,j,n) {
				dp[i]=max(dp[i-1],pre[i-1])+arr[i];
				pre[i-1]=tmp;
				tmp=max(tmp,dp[i]);
			}
		}
		printf("%lld
", tmp);
	}
	return 0;
}