UVA 12307 Smallest Enclosing Rectangle

https://vjudge.net/problem/UVA-12307

题目

给一些点，求包含这些点的面积最小的和周长最小的长方形的面积。

题解

显然，包含这些点就是包含这些点的凸包，然后可以证明满足周长或面积最小的长方形一定过凸包的一条边。

不会直接证明= =可以用反证法

如果不过任意一条边，那么多边形与长方形就有三种关系：有2、3、4个点在长方形上

 

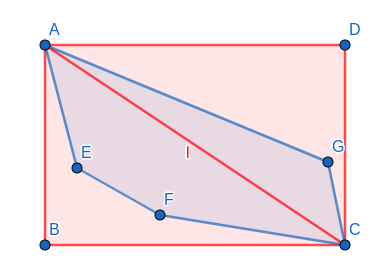
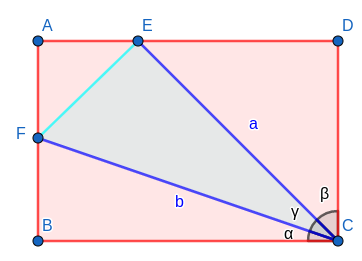
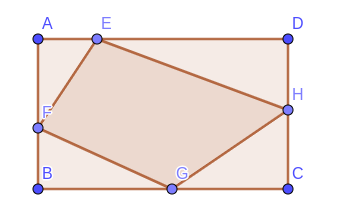
设其中的边长为已知，通过角度关系，可以证明长$AD$和宽$AB$的和（配角公式）与积（积化和差）与夹角成单峰函数，夹角范围是$[0,frac{pi}{2}]$，于是一定过一条边时取最小

参考一个求解多边形最小面积外接矩形的算法 - 图文 - 百度文库

于是可以参考旋转卡壳，选出到一条边距离最长的点，最左边的点和最右边的点，并且边旋转时，这些点也会跟着旋转，于是可以降到$O(n)$

加上凸包$O(nlog n)$

AC代码

#include<cstdio>
#include<cmath>
#include<cctype>
#include<map>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;

#define REP(i,a,b) for(register int i=(a); i<(b); i++)
#define REPE(i,a,b) for(register int i=(a); i<=(b); i++)
#define PERE(i,a,b) for(register int i=(a); i>=(b); i--)

#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__),fflush(stdout)
#else
#define DBG(...) (void)0
#endif

template<class T>
inline void read(T&x) {
	static int si; static char ch;
	x=0,si=1; do ch=getchar(); while(!isdigit(ch)&&ch!='-');if(ch=='-') si=-1, ch=getchar(); while(isdigit(ch)) {x=x*10+ch-'0'; ch=getchar();}x*=si;
}
template<class T, class...A> inline void read(T&t,A&...a){read(t); read(a...);}
#define D Point
#define CD const Point
template<class T,int Z> struct Arr {
	T data[Z];int n;
	inline T& operator[](int a) {return data[a];}
	inline void push(const T&x) {data[n++]=x;}
	inline void pop() {n--;}
};

#define EPS 1e-9
inline int dcmp(double x) {return fabs(x)<EPS?0:(x<0?-1:1);}

struct Point {
	double x,y;
	};
	bool operator<(CD&l, CD&r) {return dcmp(l.x-r.x)<0 || (dcmp(l.x-r.x)==0 && dcmp(l.y-r.y)<0);}
	bool operator==(CD&l, CD&r) {return dcmp(l.x-r.x)==0 && dcmp(l.y-r.y)==0;}
	D operator+(CD&l, CD&r) {return (D){l.x+r.x,l.y+r.y};}
	D operator-(CD&l, CD&r) {return (D){l.x-r.x,l.y-r.y};}
	D operator/(CD&l, double a) {return (D){l.x/a,l.y/a};}
	D operator*(CD&l, double a) {return (D){l.x*a,l.y*a};}
	D operator*(double a, CD&l)  {return (D){l.x*a,l.y*a};}
	double dot(CD&l, CD&r) {return l.x*r.x+l.y*r.y;}
	double cross(CD&l, CD&r) {return l.x*r.y-l.y*r.x;}
	double len(CD&l) {return sqrt(l.x*l.x+l.y*l.y);}

#undef D
#undef CD

#define MAXN 100007
typedef Arr<Point,MAXN> Plg;

void convex(Plg&p, Plg &ch) {
	sort(p.data,p.data+p.n);
	int &m=ch.n; m=0;
	REP(i,0,p.n) { while(m>1 && cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)m--;ch[m++]=p[i];}
	int k=m;
	PERE(i,p.n-2,0) {while(m>k && cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)m--;ch[m++]=p[i];}
	if(p.n>1) m--;
}

double area(Plg&p) {
	double ans=0;
	REP(i,0,p.n) {
		ans+=cross(p[i],p[(i+1)%p.n]);
	}
	return ans;
}

Plg a,b;

int main() {
	int n;
	while(~scanf("%d", &n) && n) {
		REP(i,0,n) {
			scanf("%lf%lf", &a[i].x, &a[i].y);
		}
		a.n=n; convex(a,b);
		double S=2e33,L=2e33;
		b[b.n]=b[0]; int v=1; int lm, rm=0; bool fi=false;
		REP(u,0,b.n) {
			while(1) {
				double dt=cross(b[u+1]-b[u],b[v+1]-b[v]);
				if(dt<=0) {
					break;
				}
				v++;
				if(v>=b.n) v=0;
			}
			if(!fi) fi=true,lm=v;
			while(1) {
				double ds=dot(b[u+1]-b[u],b[lm+1]-b[lm]);
				if(ds>=0) break;
				lm++;
				if(lm>=b.n) lm=0;
			}
			while(1) {
				double ds=dot(b[u+1]-b[u],b[rm+1]-b[rm]);
				if(ds<=0) break;
				rm=(rm+1)%b.n;
				if(rm>=b.n) rm=0;
			}
			double z=len(b[u+1]-b[u]);
			double l=dot(b[u+1]-b[u],b[rm]-b[lm])/z;
			double h=cross(b[u+1]-b[u],b[v]-b[u])/z;
			S=min(S,l*h);
			L=min(L,(l+h)*2);
		}
		printf("%.2lf %.2lf
",S,L);
	}
}