第二章
2.1视觉感知要素
2.1.1 人眼的结构

眼睛由角膜与巩膜外壳、脉络膜和视网膜包围,晶状体由通信的纤维细胞层组成,并由附在睫状体上的纤维悬挂;视网膜上分布两类光感受器(锥状体和杆状体),他们主要位于中央凹附近,对颜色高度敏感。其中锥状体视觉称为白昼视觉或亮视觉;杆状体没有色彩感觉,对低照明度敏感,当只有杆状体受刺激时(月光下),称为暗视觉或微光视觉。
*低照明水平下,主要有杆状体执行;高照明水平下,主要有锥状体执行。
2.1.2 眼睛中图像的形成
光接收器的相对刺激作用产生感知,把辐射能转变为电脉冲,最后由大脑解码。
2.1.3 亮度适应和辨别
由人的视觉系统感知的亮度是主观亮度,视觉系统具有亮度适应现象(通过改变整个灵敏度来完成这一较大的变动),视觉系统当前灵敏度级别称为亮度适应级别。
在背景光强I的视野中增加一个照射分量ΔI,形成一个持续时间很短的闪烁,ΔI/I称为韦伯比,其值较小意味着可分辨强度较小的百分比变化,表明辨别能力"较好"。
表明感知亮度不是简单强度的函数的两种现象:马赫带,在强度不同的区域边界出现"下冲"或"上冲"现象;同时对比,感知区域的亮度并不简单的取决于其强度,与背景亮度也有关系。下面给出了这两个现象的例子。


2.2 光和电磁波谱
电磁波可以看成以波长λ传播的正弦波,每个无质量的粒子包含一定的能量,其称之为光子。可见光波段在整个电磁波谱中占相当窄的一部分,彩色谱的每种颜色不是突然中止的,而是混合平滑过渡到另外一种颜色。没有颜色的光称之为单色光或五色光,唯一属性是它的强度或大小,灰度级一词通常用来表示单色光的强度。
*从黑到白的单色光的度量值范围称为灰度级,单色图像通常称之为灰度图像。

描述彩色光源:发光强度,从光源流出能量的总量,用瓦特(W)度量;光通量,描述观察者从光源感受到的能量,用流明数(lm)度量;亮度,一种主观描述。
2.3 图像感知和获取
2.3.1 使用单个传感器获取图像
2.3.2 使用条带传感器获取图像
2.3.3 使用传感器阵列获取图像
2.3.4 简单的图像形成模型
我们用形如f(x, y)的二维函数来表示图像,在空间坐标(x, y)处,f的值或幅度是一个正的标量,其物理意义由图像源决定,因为其亮度与物理源的辐射能量有关, f一定是一个非零有限量

函数可以由两个分量来表征:入射到被观察场景的光源总能量和场景中物体反射的光的总能量(有时候用投射来替代反射)。这两个分量分别称为入射分量和反射分量,分别用来表示,则

对于单色图像的任意坐标的灰度可以表示为l=f(x, y),其值范围是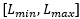 。这区间称为灰度级,通常情况下是[0, L - 1],最小值为黑色,最大值为白色。
。这区间称为灰度级,通常情况下是[0, L - 1],最小值为黑色,最大值为白色。
2.4 图像取样和量化
我们将连续的感知数据转换为数字形式有两步处理:取样和量化。
2.4.1 取样和量化的基本概念
对坐标值的数字化称之为取样,对灰度值的离散化称之为量化。

2.4.2 数字图像表示
通过取样和量化,我们可以把一幅图像函数转换为数字图像,其坐标张成的实平面部分称为空间域,x和y称之为空间变量或空进坐标。
一副数字图像可以用三种方式进行标示:
- 函数图:x和y是空间坐标,z是f在此坐标处的值。
- 灰度图:每个点的灰度值与该点的f值成正比,当图像的一部分被打印并作为数值进行分析时,这种表示相当有用。
- 矩阵:可以直接进行处理和算法开发。
用矩阵表示时,矩阵中每个元素是将图像单元、图像元素或像素,注意数字图像的远点位于左上角,出于存储和量化硬件的考虑,灰度级数典型地取2的整数次幂,即 ,灰度跨越的值域非正式的称谓动态范围,作为一条规则,上限取决于饱和度,下限取决于噪声。与这一概念紧密联系的是图像对比度,我们定义一幅图像中最高和最低灰度级间的灰度差为对比度。饱和度指超过这个值的灰度级将被剪切掉这样的一个最高值,噪声表现为粒状的纹理模式,在较暗区域掩盖了可检测的最低真实灰度级。
,灰度跨越的值域非正式的称谓动态范围,作为一条规则,上限取决于饱和度,下限取决于噪声。与这一概念紧密联系的是图像对比度,我们定义一幅图像中最高和最低灰度级间的灰度差为对比度。饱和度指超过这个值的灰度级将被剪切掉这样的一个最高值,噪声表现为粒状的纹理模式,在较暗区域掩盖了可检测的最低真实灰度级。
2.4.3 空间和灰度分辨率
空间分辨率是图像中可分辨最小细节的度量,每单位距离线对数和单位距离点数是最长用的度量,要注意的是空间分辨率的度量必须针对空间单位来规定才会有效。
灰度分辨率是在灰度级中可分辨的最小变化。
2.4.4 图像内插
内插是在诸如放大、收缩、旋转和几何校正等任务中广泛应用的基本工具,从根本上看,内插是用已知数据来估计未知位置的数值的处理。如将一副500×500的图像放大到750×750的图像。
最简单的方法是最近邻内插法,将原图像中最近邻的灰度赋值给每个新的位置;常用的是双线性内插法,用4个最近邻去估计给定位置的灰度,但它并不是一种线性方法,公式如下:

更复杂的是双三次内插,包括16个最近邻点。它是商业图像编辑程序的标准内插方法,公式为:

2.5 像素间的基本关系
本书中,图像用f(x, y)表示,某个特殊的像素用小写字母表示,如或者。
2.5.1 相邻像素
像素p的4邻域:(x+1, y) (x-1, y) (x, y+1) (x, y-1),这四点称之为p的邻点,用 表示;p的四个对角邻点用
表示;p的四个对角邻点用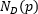 表示;这8个点称为p的8邻域,用
表示;这8个点称为p的8邻域,用 表示。如果p在边界上,在第三章进行处理。
表示。如果p在边界上,在第三章进行处理。
2.5.2 邻接性、连通性、区域和边界

邻接性分为4邻接、8邻接和m邻接(又称m邻接);令S是贴图想中的一个像素子集,若S的全部像素之间存在一个通路,则可以说两个像素p和q在S中是连通的,对于S中任意像素p,S中连通到该像素的集称为S的连通分量,若S仅有一个连通分量,则S称为连通集。
令R为图像中的一个子集,若R为连通集,则称R为一个区域。
区域R的边界(边缘或轮廓)是这样一些点的集合:这些点与R的补集中的点邻近,这种边界也成为内边界。
2.5.3 距离度量
对于坐标分别为(x, y)(s, t) (v, w)的像素p, q, z,若

则D 称为距离函数或度量;像素p, q的距离定义如下:

2.6 数字图像处理中所用数学工具介绍
http://v.163.com/special/opencourse/daishu.html,这是网易公开课--MIT的线性代数,Gilbert Strang教授讲得很有应用性。
2.6.1 阵列与矩阵操作
2.6.2 线性操作与非线性操作
线性操作针对的是加和操作和数乘操作。
2.6.3 算术操作
值得是两个矩阵点对点做数学运算,图像相加可以做平滑噪声的处理,图像相减可以增强差别,图像相乘或相除可以用来矫正阴影和进行模板操作。
*均值为$m$的随机变量$z$的方差定义为$E[(z-m)^2]$,其中$E{}$是该参量的期望值;两个随机变量的协方差定义为$E[(z_i-m_i)(z_j-m_j)]$,若两个变量不相关,则它们的协方差为0。
2.6.4 集合和逻辑操作
基本集合操作
属于、空集、交集、并集、补集的基本概念与数学中学的类似,还有一个差集的概念:
$$A-B=\{w|w\in A,\,w\notin B\}=A\cap{B^c}$$
图像灰度集合操作中会有些小的变化,首先元素是三元形式$(x, y, z)$,其中$x, y$是空间坐标,$z$是灰度,那么补集定义$A^c=\{(x, y, K-z)|(x, y, z)\in A\}$,并集定义$A\cup B=\{\mathrm{max}_z(a,b)|a\in A,b\in B\}$等等。
逻辑操作
包括的操作有非(NOT)、与(AND)、或(OR)、与非(做差集AND[NOT])和异或(XOR)操作,其中需要注意的是AND, OR, NOT是功能完备的。
模糊集合
用以处理界限不精确的分类集合,比如用年龄区分。
2.6.5 空间操作
空间操作可以分作三类:
单像素操作:
$$s=T(z)$$
其中$z$是源图像中某像素的灰度,$s$是处理后图像中相应的灰度,$T$是变换函数。
邻域操作
令$S_{xy}$代表图像$f$中任意一点$(x,y)$为中心的一个邻域坐标集,然后在这个邻域内经过一些操作生成一个像素的坐标值。
几何空间变换和图像配准
几何变换也叫橡皮膜变换,它由两个基本操作组成:坐标空间变化+灰度内插(空间变换之后的像素赋灰度值)。
最常用的空间坐标变换是仿射变换,形式如下:
$$\begin{bmatrix} x & y & 1 \end{bmatrix}=\begin{bmatrix}v & w & 1 \end{bmatrix}T=\begin{bmatrix} v & w & 1 \end{bmatrix}\begin{bmatrix} t_{11} & t_{12} & 0\\ t_{21} & t_{22} & 0 \\ t_{31} & t_{32} & 0 \end{bmatrix}$$
其中矩阵$T$可以实现恒等变换、尺度变换、旋转变换、平移变换、以及垂直和竖直方向的便宜变换。对于$T$中的元素,$t_{11}$ 和$t_{22}$表明尺度变换因子,$t_{12}$表明水平偏移变换,$t_{21}$表明垂直偏移变换,$t_{31}$和$t_{32}$表明平移变换情况。
上式可以有两种方法来使用,一种是向前映射,一种是逆计算,称作反向映射,即$(v,w)=T^{-1}(x,y)$的,就实现角度来讲,往往反向映射更为有效。
图像配准是数字图像处理的一种重要应用,用于对齐多幅相同场景的图像。这多幅图像可能是多模态的,使用的方法是利用约束点。往往约束点选取的越多,其准确度也越高,但计算量会相应增加。
2.6.6 向量与矩阵操作
一个像素可以用向量来表示,如RGB彩色图像;一幅图像也可以用向量来表示,即一个$M\times N$的矩阵变为$MN\times 1$的向量。
对于用矩阵表示的像素,任一点$a$在$n$维空间的欧氏距离$D$可以表示为:
$$D(\vec{z},\vec{a})=\begin{bmatrix}(\vec{z}-\vec{a})^T(\vec{z}-\vec{a})\end{bmatrix}^{\frac{1}{2}}=\sum_{i=1}^{n}{(z_i-a_i)^2}^{\frac{1}{2}}$$
2.6.7 图像变换
一种二维线性变换$T(u,v)$可以表示为
$$T(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)r(x,y,u,v)$$
其中$f(x,y)$是图像,$r(x,y,u,v)$称为正变换核,如果从$T$到$f$,需要的变换核称为反变换核,这两种变换在一起称为变换对。对于变换核,如果可以拆分,如
$$r(x,y,u,v)=r_1(x,u)r_2(r,v)$$
那么我们称变换核是可分的,如果$r_1=r_2$,那么变换是对称的,例如二维傅里叶变换
$$r(x,y,u,v)=e^{-j2\pi(\frac{ux}{M}+\frac{vy}{N})}$$

上图描述了线性变换域执行图像处理的基本步骤,变换可以看作一个变换举矩阵作用到图像矩阵上。
2.6.8 概率方法
随机变量$z$的第$n$阶矩定义为:
$$\mu_n(z)=\sum_{k=0}^{L-1}(z_k-m)^np(z_k)$$
其中$p(z_k)$是图像中灰度级$z_k$出现的概率,$m$为整幅图像的灰度均值,所以我们可以得到$\mu_0(z)=1$,表示概率之和为1;$\mu_1(z)=m$,表示整幅图像的期望值;$\mu_2(z)=\sigma^2$,表示方差。
*高阶矩的敏感性更高,对于图像的视觉特性也有越明显的作用。
MATLAB 版
这一章节主要是一些概念介绍和函数介绍。
2.1 数字图像的表示
2.1.1 坐标约定
IPT(Image Process Tools)中关于坐标的描述与数学上的描述略有不同,主要区别有:
- 使用$(r,c)$来代表行和列。
- 远点在$(1,1)$处。
MATLAB的基本单位是矩阵,对于一个数来说,可以看做是$1\times 1$的标量,一副数字图像可以表示成:
$$f=\begin{bmatrix}f(1,1) & f(1,2) & \cdots & f(1,N) \\ f(2,1) & f(2,2) & \cdots & f(2,N) \\ \vdots & \vdots & \ddots & \vdots \\ f(M,1) & f(M,2) & \cdots & f(M,N) \\\end{bmatrix}$$
一个$1\times N$矩阵称为一个行向量,一个$M\times 1$矩阵称为一个列向量。
2.2 读取图像
imread - Read image from graphics file.
用法:f = imread('路径名+文件名+扩展名')
其支持的格式有

size – Size of array.给出一幅图像的行数和列数
用法:[M, N] = size(f)
whos - List current variables, long form. 显示出一个数组的附加信息
用法:whos f
2.3 显示图像
imshow - Display image in Handle Graphics figure.
用法:imshow(f, G)
其中G是该图像的灰度级数,默认是256,用一个数组表示[low high],如果参数不写,那么会将整幅图像的像素灰度值等比例拉伸到0-255,如下图效果:


Figure - Create figure graphics object. 用以显示多福图像时辅助使用。
用法:imshow(f), figure, imshow(g)
2.4 保存图像
Imwrite - Write image to graphics file.
用法:imwrite(f, '路径名+文件名+扩展名')
针对JPEG图像使用imwrite,可以通过调整最后一个缺省参数达到压缩效果:
用法:imwrite(f, '路径名+文件名+扩展名', q)
其中的q是一个0-100之间的整数,q越小,图像退化越严重。
其支持的格式有

imfinfo - Information about graphics file.
用法:k = imfinfo ('路径名+文件名+扩展名')
此时的k可以看做一个结构体(针对C语言),具体显示可以使用"."操作符,如k.Filename。
round – Round to nearest integer.
用法:m = round(x)
2.5 数据类
MATLAB默认的数据类型是double,其支持的数据类有


2.6 图像类型
支持四种图像类型:亮度图像、二值图像、索引图像、RGB图像。
2.6.1亮度图像
类型有unit8 ,范围是[0, 255];unit16,范围[0, 65535];double,归一化之后范围[0, 1]。
2.6.2 二值图像
其像素取值只能是0或者1。
logical – Convert numeric values to logical
用法:B = logical(A)
islogical - Determine if input is logical array
用法:tf = islogical(A)
如果是二值图像,返回1,;如果不是,返回0。
2.7 数据类与图像类型间的转换
2.7.1 数据类型间转换
语法简单:B = data_class_name(A);比如B = double(A)。
*从double到Unit8的时候,小于0的全部置为0,大于255的置于255,其他部分向下取整。
2.7.2 图像类和类型间的转换
mat2gray - Convert matrix to grayscale image.
im2bw – Convert image to binary image, based on threshold.
im2double – Convert image to double precision.
等等函数,其中用关系运算符也可以生成二值图像,如
$$f=\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix} \ f > 2 : \ \begin{bmatrix} 0 & 0 \\ 1 & 1 \end{bmatrix}$$
2.8 数组索引
2.8.1 向量索引
转置运算符(.'),可以将行向量转置为列向量;取元素的数据块可以使用冒号操作符(:);end表示向量的最后一个元素
linspace – Generate linearly spaced vectors
用法:x = linspace(a, b, n)
产生一个含有n个元素的行向量x,这n个元素线性地隔开并且包含a与b。
2.8.2 矩阵索引
example:
$$A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$$
使用end作为索引:$B = A(2 : end, end : -2 :1)$,得到的结果为$\begin{bmatrix} 6& 4 \\ 7 & 9 \end{bmatrix}$,是因为从行方向上看取第2行至第3行;从列方向上看,从最后一行至第1行间隔取。
使用向量作为索引:$C = A([1 3], [2 3])$,得到的结果为$\begin{bmatrix} 2 & 3 \\ 8 & 9 \end{bmatrix}$,是因为行方向取1,3行,列方向取2,3列。
矩阵索引还可以使用寻址方式,形式为$A(D)$,其中D是一个逻辑数组,例如$\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 1\\ 0 & 0 & 0 \end{bmatrix}$,那么$A(D) = \begin{bmatrix} 1 \\ 6\end{bmatrix}$
使用冒号,会将交矩阵所有元素按照列方向排成一个列向量,比如$E = B(:)$可以得到结果$E = \begin{bmatrix}1 \\ 4 \\ 7 \\ 2 \\ 5 \\ 8 \\ 3 \\ 6 \\ 9 \end{bmatrix}$
sum – Sum of array elements
用法:sum(A)
可以得到的结果是 $\begin{bmatrix}12 & 15 & 18\end{bmatrix}$
2.8.3 选择数组维数
Operation(A, dim)
operation是一个可能的操作, A是一个数组,dim是一个标量,表明沿着第dim维给出相应结果。
ndims – Number of array dimensions
用法:ndims(A)
其结果不会小于2,因为即使是标量,我们也认为是个$1\times 1$的数组。
2.9 一些重要的标准数组
$zeros(M,N)$生成一个大小$M\times N$的double类数组,其元素均为0。
$ones(M,N)$生成一个大小$M\times N$的double类数组,其元素均为1。
$true(M,N)$生成一个大小$M\times N$的logical类数组,其元素均为1。
$false(M,N)$生成一个大小$M\times N$的logical类数组,其元素均为0。
$magic(M)$生成一个大小$M\times M$的魔方数组,每一行元素之和、每一列元素之和和主对角线元素之和相等,主要用于测试目的,且元素均为整数。
$rand(M,N)$生成一个大小$M\times N$的double类数组,其元素在[0, 1]之间。
$randn(M,N)$生成一个大小$M\times N$的double类数组,其元素是正态分布的随机数,随机数均值为0,方差为1,如高斯分布。
2.10 M函数编程简介
2.10.1 M文件
M文件可以是简单执行一系列MATLAB语句的脚本,也可以是接受变量并产生一个或多个输出的函数。
函数的定义形式:
$$function [outputs] = name(inputs)$$
2.10.2 运算符
三类运算符:
- 执行数值计算的算术运算符
- 在数量上比较操作数的关系运算符
- 执行函数AND、OR和NOT的逻辑运算符
算术运算符
*点操作符,比如".^"、".*"都是点对点操作,两个操作数必须是相同的维数。
关系运算符
作用于两个相同维数的矩阵,点对点进行关系判断。其中"非"是"~="
逻辑运算符和函数
AND:"&" OR:"|" NOT:"~"
逻辑函数:
- xor(异或):作用于两个相同维数的数组
- all:若一个向量中所有元素都非零,则返回1。矩阵中按列操作。
- any:若一个向量中任何元素都非零,则返回1。矩阵中按列操作。
一些重要的变量和常量

数的表示
可以使用科学技术规则。
2.10.3 流控制
if, else , else if:
if expression1
statements
elseif expression2
statements
else
statements
end
for:
for index = start: increment: end
statement
end
switch
switch switch_expression
case case_expression
statement
case case_expression
statement
otherwise
statement
end
如果case中有多个表达式,用花括号;且与C语言的switch相比,不需要break语句。
2.10.4 优化代码
- 向量化代码:将循环问题变成向量或矩阵预算。
- 预分配内存:计算开始前就分配足够的空间内存。
2.10.5 交互式I/O
input – Request user input.
disp – Display text or array.
strread – Read formateed data from string.
strcmp – Compare strings(case sensitive)
2.10.6 单元数组与结构简介
单元数组:是一个多维数组,其元素是其他数组元素的副本。(MATLAB中的赋值并不是做一个副本,而是做一个标号,除非原始数组发生了变化)比如$C={A, B}$之后数组A、B可能会改变,但C中不会跟着相应改变。
结构:类似单元数组,更接近于C语言中的结构体。