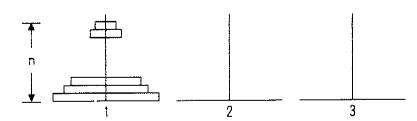
将所有盘子从木桩1移到木桩3,移动规则如下:
1、每次只能移动一个盘子,而且只能从最上面的盘子搬动。
2、任何盘子可以搬到任何一根木桩。
3、必须维持盘子的大小是由上而下依次递增。
解决思路: 数学归纳法,即盘子n=1,n=2,n=3情况下的盘运过程。
从中你可以总结出一个数学公式或通用搬运过程。
使用数学公式,你会直接得出次数。这和老老实实去搬相比得出搬运次数。是一个捷径。最后结果是殊路同归,但缺少愚公移山的过程。
所以,通用搬运过程,可以展示具体的搬运过程,可以从过程得出结果。这就是算法,也就是计算机科学与数学的区别。
通用搬运过程:
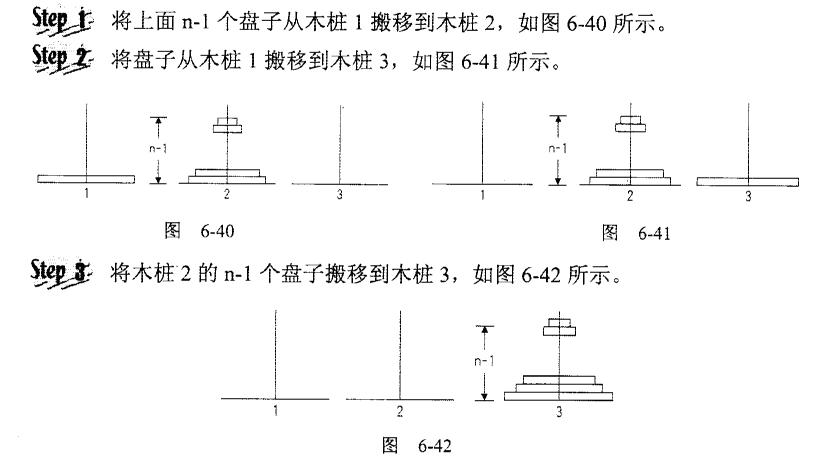
Step1.将上面n-1个盘子从木桩1搬移到木桩2.
Step2.将盘子从木桩1搬移到木桩3.
Step3将木桩2的n-1个盘子搬移到木桩3.
是不是有点如何把大象塞进冰箱的味道呢?
代码是不是有点迷惑呢?
第15行是第一步骤,也就是将上面n-1个盘子从木桩1搬移到木桩2.
hanoi(dishs - 1,peg1,peg3,peg2);/* 第一步骤 */
第17行是第三步骤,也就是将木桩2的n-1个盘子搬移到木桩3.
hanoi(dishs - 1,peg2,peg1,peg3);/* 第三步骤 */
这样不去理解代码,而去记住代码,是不是方便些?
如果汉诺塔的问题变异了:
如果再变异成有n个盘子和n根柱子,求出最少移动次数,最多移动次数,指定移动次数的移动过程。你能写吗?
能。从汉诺塔的本质出发。汉诺塔的本质就是一个过程:首先算固定盘子和固定柱子的移动次数,从中推导出n个盘子和固定柱子的移动次数,从中推导出n个柱子和固定盘子的移动次数。继而推导出n个盘子和n跟柱子的移动次数。至于指定移动次数的移动过程,就有点九阴真经的味道了。
我们可以看到,汉诺塔的本质有点宏观上的数学归纳法。
以上纯属我扯淡,大家娱乐下就行。