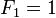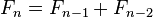斐波拉契数列

写一个函数，输入n，其斐波那契数列的第n项。

  斐波那契数列的定义如下：

• 
• 
• 

#include "stdafx.h"
#include<iostream>
using namespace std;


//方法1 递归  缺点：效率低 
long long Fibonacci_Solution1(unsigned int n )
 {
     if(n <= 0)
         return 0;

     if( n == 1)
         return 1;

     return Fibonacci_Solution1(n-1) + Fibonacci_Solution1(n-2);
 }

//方法2 循环 
 long long Fibonacci_Solution2(unsigned int n)
 {
     int result[2] = {0,1};
     if(n < 2)
         return result[n];

     long long fibNMinusOne = 1;
     long long fibNMinusTwo = 0;
     long long fibN = 0;

     for(unsigned int i = 2 ; i <= n ; ++i)
     {
         fibN = fibNMinusOne + fibNMinusTwo;

         fibNMinusTwo = fibNMinusOne;
         fibNMinusOne = fibN;
     }

     return fibN;
 }
 
 //方法3 循环 其实和方法2差不多 
 long long Fibonacci_Solution3(unsigned int n)
 {
     if(n <= 0)
         return 0;
     else if(n == 1)
         return 1;
     else
     {
         int *array = new int[n+1];
         array[0] = 0;
         array[1] = 1;
         for(int i = 2; i<= n; i++)
             array[i] = array[i-1] + array[i-2];

         int result = array[n];
         delete[] array;

         return result;
      }
 }

//方法4 数学归纳法 略

 
 int main()
 {
     int num1 = Fibonacci_Solution1(30);
     int num2 = Fibonacci_Solution2(30);
     int num3 = Fibonacci_Solution3(30);
     
     cout << num1 <<endl;
     cout << num2 <<endl;
     cout << num3 <<endl;
    
    return 0;
 }

 运行结果如下: