源于博客
GBRT(梯度提升回归树)有好多名字,标题全是它的别名。
它是一种迭代的回归树算法,由多棵回归树组成,所有树的结论累加起来得到最终结果。在被提出之初与SVM一起被认为是泛化能力较强的算法。
主要由三个概念组成:回归决策树Regression Decistion Tree(即DT),梯度提升Gradient Boosting(即GB),Shrinkage 。搞定这三个概念后就能明白GBDT是如何工作的,要继续理解它如何用于搜索排序则需要额外理解RankNet概念,之后便功德圆满。下文将逐个碎片介绍,最终把整张图拼出来。
1. DT:回归树Regression Decistion Tree
决策树分为两大类:回归树和分类树,前者用于预测实数值,如明天的温度,用户年龄,网页相关程度等,后者用于分类标签值,如用户性别、晴天/阴天/雨、网页是否是垃圾页面等。注意到前者的结果的加减是有意义的,后者则无意义。GBRT的核心在于累加所有树的结果作为最终结果,对于分类树的结果是无法累加的,从而,GBDT中的树都是回归树,不是分类树。
下面以性别判别/年龄预测(每个例子都是已知性别/年龄的人,而特征包括这个人上网的时长、上网的时间段、网购所花金额等)来说明回归树如何工作:
先说一下分类树,分类树在每次分枝时,是穷举每一个特征的每一个阈值,找到使得(阈值<特征)(特征<=阈值)分成的两个分枝的熵最大的特征和阈值(熵最大的概念可理解成尽可能每个分枝的男女比例都远离1:1),按照该标准分枝得到两个新节点,用同样的方法继续分枝直到所有人都被分入性别唯一的叶子节点,或达到预设的终止条件,若最终叶子结点中的性别不唯一,则已多数人的性别作为该叶子节点的性别。
回归树总体流程也是类似,不过在每个节点(不一定是叶子节点)都会得一个预测值,以年龄为例,该预测值等于属于这个节点的所有人年龄的平均值。分枝时,是穷举每一个特征的每一个阈值找到最好的分割点,衡量的标准改为最小化均方差(而不是最大熵),即(每个人的年龄-预测年龄)平方和除以n。分枝直到每个叶子节点上人的年龄都唯一(这太难了)或者达到预设的终止条件(如叶子个数上限)。若最终叶子结点上年龄不唯一,则以该节点上所有人平均年龄作为预测年龄。
2. GB:梯度提升Gradient Boosting
Boosting,迭代,即通过迭代多棵树来共同决策,每棵树的结论并不是年龄本身,而是年龄的一个累加量。GBRT的核心就在于,每一棵树学的是之前所有树的结论和的残差,这个残差就是一个加上预测值后能得真实值的累加量。比如,一个人的真实年龄是18岁,但是第一棵树预测年龄是12岁,差了6岁,残差为6;那么第二棵树我们把其年龄设为6岁去学习,如果第二棵树真的能把其分到6岁的叶子节点,那么累加两棵树的年龄就是真实值,如果第二棵树的结论是5岁,仍剩余1岁的残差,需要继续学习。
3. Boost与Gradient boost:提升与梯度提升
原始的Boost算法是在算法开始的时候,为每一个样本赋上一个权重值,初始的时候,大家都是一样重要的。在每一步训练中得到的模型,会使得数据点的估计有对有错,我们就在每一步结束后,增加分错的点的权重,减少分对的点的权重,这样使得某些点如果老是被分错,那么就会被“严重关注”,也就被赋上一个很高的权重。然后等进行了N次迭代(由用户指定),将会得到N个简单的分类器(basic learner),然后我们将它们组合起来(比如说可以对它们进行加权、或者让它们进行投票等),得到一个最终的模型。
而Gradient Boost与传统的Boost的区别是,每一次的计算是为了减少上一次的残差(residual),而为了消除残差,我们可以在残差减少的梯度(Gradient)方向上建立一个新的模型。所以说,在Gradient Boost中,每个新的模型的简历是为了使得之前模型的残差往梯度方向减少,与传统Boost对正确、错误的样本进行加权有着很大的区别
4. GBDT工作实例
还是年龄预测,简单起见训练集只有4个人A/B/C/D,他们的年龄分别是14,16,24,26。其中A和B分别是高一、高三学生;C和D分别是应届毕业生和工作两年的员工,如果用一棵传统的回归决策树来训练,会得到如下图1所示的结果:
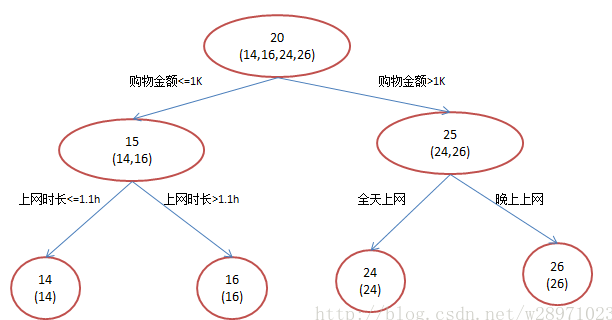
现在使用GBDT来做这件事,由于数据过少,限定的叶子结点最多有两个,即每棵树都只有一个分枝,并且限定只学两棵树,我们会得到以下结果:
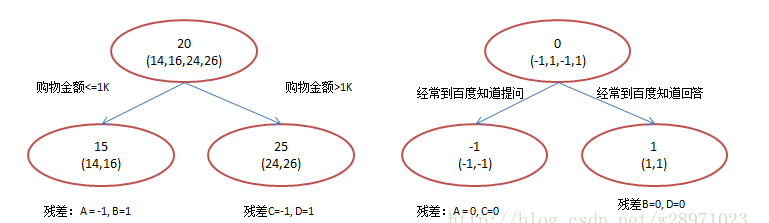
在第一棵树分枝和图1一样,由于A,B年龄较为相近,C,D年龄较为相近,他们被分为两拨,每拨用平均年龄作为预测值。此时计算残差(残差的意思就是: A的预测值 + A的残差 = A的实际值),所以A的残差就是16-15=1(注意,A的预测值是指前面所有树累加的和,这里前面只有一棵树所以直接是15,如果还有树则需要都累加起来作为A的预测值)。进而得到A,B,C,D的残差分别为-1,1,-1,1。然后我们拿残差替代A,B,C,D的原值,到第二棵树去学习,如果我们的预测值和它们的残差相等,则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的,第二棵树只有两个值1和-1,直接分成两个节点。此时所有人的残差都是0,即每个人都得到了真实的预测值。
很容易发现几个问题:
1)既然上面两个方法最终效果相同,为何还需要GBDT呢?
过拟合。过拟合是指为了让训练集精度更高,学到了很多“仅在训练集上成立的规律”,导致换一个数据集当前规律就不适应了。其实只要允许一棵树的叶子结点足够多,训练集总是能够训练到100%准确率的。
我们发现方法1为了达到100%精度使用了3个feature(上网时长、时段、网购金额),其中分枝“上网时长>1.1h” 很显然已经过拟合了,这个数据集上A,B也许恰好A每天上网1.09h, B上网1.05小时,但用上网时间是不是>1.1小时来判断所有人的年龄很显然是有悖常识的;
相对来说方法2的boosting虽然用了两棵树 ,但其实只用了2个feature就搞定了,后一个feature是问答比例,显然图2的依据更靠谱。Boosting的最大好处在于,每一步的残差计算其实变相地增大了分错instance的权重,而已经分对的instance则都趋向于0。这样后面的树就能越来越专注那些前面被分错的instance。
2)这个不是boosting吧,Adaboost不是这么定义的
这是boosting不是Adaboost。Adaboost是另一种提升方法,它按分类对错,分配不同的权重,使用这些权重计算cost function,从而让错分的样本权重越来越大,使他们更被重视。Bootstrap也有类似思想,它在每一步迭代时不改变模型本身,也不计算残差,而是从n个例子训练集中按照一定的概率重新抽取n个例子出来,对这n个新的例子再训练一轮。GBDT也可以在使用残差的同时引入Bootstrap re-sampling,GBDT多数实现版本中也增加的这个选项,但是否一定使用则有不同看法。re-sampling一个缺点是它的随机性,即同样的数据集合训练两遍结果是不一样的,也就是模型不可稳定复现,这对评估是很大挑战,比如很难说一个模型变好是因为你选用了更好的feature,还是由于这次sample的随机因素。