树状数组入门乱讲

树状数组入门乱讲

rt

不同于传统数组每个元素单独存放，求和时遍历相加，树状数组每个元素不单独维护，而是被维护在一个包含其他元素的前缀和里。宜先仔细揣摩后再行。

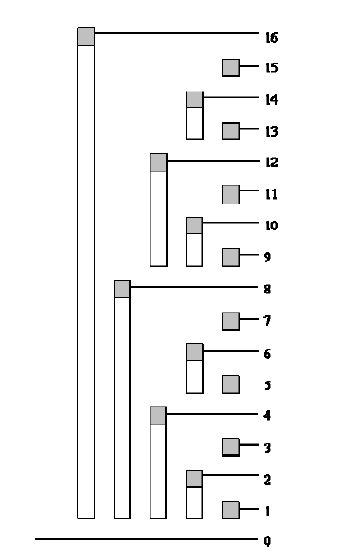
上图便体现了树状数组储存数据的原理

相当于以下等式

说明：C[]是树状数组，A[]是实际元素

C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

如此存储，便可以体现出上面所说每个元素不单独维护，而是被维护在一个包含其他元素的前缀和里的维护原则，比如元素1（即(A[1])）便包含在C[1],C[2],C[4],C[8]中，而如今有一个神器lowbit(x)=x&(-x)可以依次推出所有包含元素i的(C[k])们，我们先看看1至8的lowbit值

lowbit(1)=1

lowbit(2)=2

lowbit(3)=1

lowbit(4)=4

lowbit(5)=1

lowbit(6)=2

lowbit(7)=1

lowbit(8)=8

这时你会发现一个规律：每次当前下标再加上当前下标的lowbit值便会得到下一个包含元素i的(C[k])的下标，比如第一个包含元素1的(C[k])为(C[1])，那么下一个（第二个）包含元素1的(C[k])为(C[1+lowbit(1)])，如此按照此规律循环便可访问到所有包含元素i的(C[k])们

于是下面遍历所有包含元素i的(C[k])的程序成立

void spot(int x)
{
    for(int i=x;i<=n;i+=lowbit(i))
    	//do something
}

于是你又可以在遍历的同时顺便修改一下值（又于是下面修改元素i的值的程序成立）

void add(int x, int v)
{
    for(int i=x;i<=n;i+=lowbit(i))
    	tree[i]+=v;
}

同理，你又会发现其实查询前缀和的规律也是如此，读者可以动手模拟一下

于是查询前缀和的程序又成立

int getsum(int x)
{
    int ans=0;
    for(int i=x;i>0;i-=lowbit(i))
        ans+=tree[i];
    return ans;
}

完整的树状数组板子

int lowbit(int x){return x&(-x);}
void add(int x, int v)
{
    for(int i=x;i<=n;i+=lowbit(i))
    	tree[i]+=v;
}
int getsum(int x)
{
    int ans=0;
    for(int i=x;i>0;i-=lowbit(i))
        ans+=tree[i];
    return ans;
}

以上。

本文采用 知识共享 署名-非商业性使用-相同方式共享 3.0 中国大陆 许可协议进行许可。欢迎转载，请注明出处： 转载自：Santiego的博客