位置控制原理
最近一段时间一直在忙着写官方的C型板教程,这个教程咕了两个多月没写了,现在回来把坑填完。
C型板教程的写作思路是首先介绍板子上各个外设的基本原理,讲一下cube的配置和HAL库的API,然后讲解示例工程,论详细度和专业度比我这边这个教程要强多了,语言上也比我这边写的要严谨多了哈哈哈,链接如下,希望各位关注关注。
https://github.com/RoboMaster/Development-Board-C-Examples
回归正题,RM机器人上最复杂的控制计构就是双轴云台了,赛场上的情况对双轴云台的控制稳定度与响应灵敏度双方面都提出了很高的要求,云台控制的好坏在一定程度上就能够代表一支队伍的实力。
双轴云台采用的控制算法依然是PID控制算法,关于PID控制算法的原理与实现可以看之前的博客https://www.cnblogs.com/sasasatori/p/11672918.html
但双轴云台的控制与底盘控制存在直接的区别在于,底盘是一个单环控制系统,用户对底盘的输入值为底盘的速度期望,底盘的输出也同样是速度。而云台则是一个双环控制系统,用户对云台的输入值为云台的转动角度期望,而云台电机能够直接输出的是转速。
输入是角度的期望,输出的是电机的速度。就是由于这个原因,必须多引入一级控制器,实现将角度控制转换成速度期望,然后再通过第二级控制器完成速度的闭环控制,这就是为什么云台一定要使用双环控制系统。
针对云台的控制系统的结构,我们可以画出简化的系统框图如下:
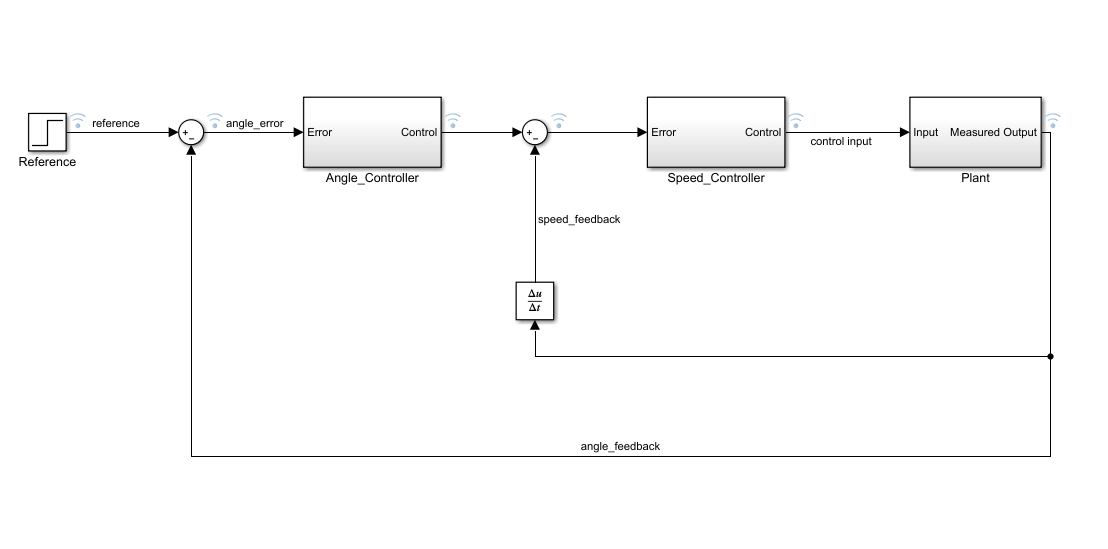
第一环控制器被称为角度控制器(Angle_Controller),因为它的输入为期望角度和实际角度之间的差值。第二环控制器被称为速度控制器(Speed_Controller),因为它的输入为期望速度和实际速度之间的差值。
我们给整个系统的输入值reference就是整个云台的角度期望,将其与实际的输出角度angle_feedback(这个值一般是云台电机编码器的反馈角度值或者IMU反馈的角度值)做差,将差值作为角度控制器(Angle_controller)的输入,计算第一环的PID,角度控制器的输出值直接作为速度控制器(Speed_Controller)的输入,输入与角速度的反馈值(一般是IMU反馈的角速度值或者将云台编码器的反馈角度值进行差分,在上面的系统图中公式(frac{△u}{△t})表示对角度值求导获得角速度)做差,得到速度控制器的输出,该输出值直接给电机。
一般第一次接触双环控制者的疑问是,为什么可以直接将角度控制器的输出作为速度控制器的输入?角度控制器的输出似乎没有什么物理含义,为什么就可以被看成是速度的期望?
从定性的角度来解释这个问题,这是因为角度控制器的输出确实在一定程度上反映了速度的期望,角度控制器的输出值越大,说明总体上角度的误差是比较大的,也就是目前的云台位置和期望的云台位置差的越远,我们就会越希望云台以更快的速度达到期望的位置,速度期望较大;而当云台的实际位置和期望位置接近时,角度控制器的输出较小,同样我们会希望云台尽可能细微的调节自身的位置,因此云台的速度期望就会小。
由此可见位置控制器的输出实际上和速度期望之间是存在正相关关系的,如果将其直接视作简单的线性关系,我们就可以直接将位置控制器的结果作为速度控制器的输入值。
当然,正相关的函数表达形式有很多,并不一定要采用线性的形式,采用线性的原因更多是因为线性的系统会更加的容易分析,如果引入非线性则系统在数学上的复杂度会增加很多。在部分工程中,我也见过使用位置控制器输出的平方或者高次幂作为速度控制器的输入的情况,这样做的好处是系统在偏差较大的位置时响应更加灵敏,而偏差较小时响应变得不灵敏,但是参数调节方面也会变得困难一些,具体使用何种方案要根据实际情况来斟酌。
在simulink中搭建仿真系统,查看系统的输出结果——输入期望为黄线reference,输出为橙线angle_feedback,可以看到系统的输出是趋于期望的,总体来说是一个稳定的系统。

这个系统同样可以信号与系统和自动控制理论的知识进行分析,实际上单环和双环的系统在分析上不会有很大的差别,不过双环控制系统不是简单将两个单环的系统函数直接相乘,速度环与位置环相互之间还是有影响的,在这里就不进行具体的数学推导了,感兴趣的同学可以仿照我在第四章中所进行的数学推导过程,假设一个电机的传递函数,然后自己建立整个系统的闭环传递函数,分析两级PID控制器各自的P,I,D参数的作用。
依然是推荐一下官方的相关教程
https://bbs.robomaster.com/thread-4941-1-1.html
https://bbs.robomaster.com/thread-5059-1-1.html
下面是一个位置随动系统的课程设计报告,其中就对这个系统做了比较详细的理论分析,对数学原理感兴趣的同学可以重点阅读。
https://wenku.baidu.com/view/0736ede9856a561252d36f14.html
可以看到报告中给出的系统结构框图实际上和我们上面给出的框图是一致的,①是位置环的PID控制器,②是速度环的PID控制器,③是电机的传递函数,④是对电机输出的位置值求微分(拉普拉斯变换后,乘一阶s因子相当于做一阶微分,除以一阶s因子相当于做一重积分)

上面这个系统的闭环传递函数如下:
有了闭环传递函数之后,这个系统的后续分析以及调节的方法就可以看报告了,系统一样的情况下,报告中所使用的分析方法同样是适用于云台的双环控制系统的。
代码示例
这里依然是采用官方代码来说明双环PID控制的代码实现,新开源的代码结构和之前的不太一样了,可读性也变强了不少,链接如下。
https://github.com/RoboMaster/RoboRTS-Firmware
云台控制的代码和底盘控制非常相似,熟悉了底盘控制代码的话应该会很容易理解。这段代码里还加了一些和模式处理相关的东西,主要还是看我用注释强调的部分的代码
void gimbal_task(void const *argu)
{
gimbal_time_ms = HAL_GetTick() - gimbal_time_last;
gimbal_time_last = HAL_GetTick();
//---------------------------------------------------
archive_index++;
if (archive_index > 99) //system delay ms
archive_index = 0;
gimbal_attitude_archive[archive_index][0] = gim.sensor.yaw_gyro_angle;//gim.pid.yaw_angle_fdb;
gimbal_attitude_archive[archive_index][1] = gim.pid.pit_angle_fdb;
gimbal_attitude_archive[archive_index][2] = gim.pid.yaw_spd_fdb;
gimbal_attitude_archive[archive_index][3] = gim.pid.pit_spd_fdb;
get_index = archive_index + 50;
if( get_index > 99)
get_index -= 100;
//----------------------------------------------------
mat_init(&yaw_kalman_filter.Q,2,2, yaw_kalman_filter_para.Q_data);
mat_init(&yaw_kalman_filter.R,2,2, yaw_kalman_filter_para.R_data);
//satori:下面这段代码是根据云台的模式进行初始化,云台的模式不同会影响角度反馈值的输入来源,pid角度的反馈值就是在下面的几个模式处理函数之一中获取的
switch (gim.ctrl_mode)
{
case GIMBAL_INIT:
init_mode_handler();
break;
case GIMBAL_NO_ARTI_INPUT:
no_action_handler();
break;
case GIMBAL_FOLLOW_ZGYRO:
closed_loop_handler();
break;
case GIMBAL_PATROL_MODE:
shoot.c_shoot_cmd = 0;
gimbal_patrol_handler();
break;
case GIMBAL_POSITION_MODE:
pc_position_ctrl_handler();
break;
case GIMBAL_RELATIVE_MODE:
pc_relative_ctrl_handler();
break;
default:
break;
}
//satori:这里是第一级PID控制器,计算yaw轴和pitch轴的角度控制输出,pid_calc的具体实现可以看第四章,其中对pid_calculate函数的详细分析
pid_calc(&pid_yaw, gim.pid.yaw_angle_fdb, gim.pid.yaw_angle_ref);
pid_calc(&pid_pit, gim.pid.pit_angle_fdb, gim.pid.pit_angle_ref);
//satori:直接将yaw轴和pitch轴第一级控制器的输出结果作为第二级速度控制器的输入
gim.pid.yaw_spd_ref = pid_yaw.out;
gim.pid.pit_spd_ref = pid_pit.out;
//satori:从传感器获取yaw轴和pitch轴的角速度反馈值
gim.pid.yaw_spd_fdb = gim.sensor.yaw_palstance;
gim.pid.pit_spd_fdb = gim.sensor.pit_palstance;
//satori:第二级PID控制器,计算yaw轴和pitch轴的角速度控制输出
pid_calc(&pid_yaw_spd, gim.pid.yaw_spd_fdb, gim.pid.yaw_spd_ref);
pid_calc(&pid_pit_spd, gim.pid.pit_spd_fdb, gim.pid.pit_spd_ref);
//satori:下面这段代码将yaw轴和pitch轴的输出结果装入控制电流的数组
/* safe protect */
if (gimbal_is_controllable())
{
glb_cur.gimbal_cur[0] = YAW_MOTO_POSITIVE_DIR*pid_yaw_spd.out;
glb_cur.gimbal_cur[1] = PIT_MOTO_POSITIVE_DIR*pid_pit_spd.out;
glb_cur.gimbal_cur[2] = pid_trigger_spd.out;
}
else
{
memset(glb_cur.gimbal_cur, 0, sizeof(glb_cur.gimbal_cur));
gim.ctrl_mode = GIMBAL_RELAX;
//pid_trigger.iout = 0;
}
yaw_angle_ref_js = gim.pid.yaw_angle_ref*1000;
yaw_angle_fdb_js = gim.pid.yaw_angle_fdb*1000;
yaw_speed_ref_js = pid_yaw.out*1000;
yaw_speed_fdb_js = gim.sensor.yaw_palstance*1000;
pit_angle_ref_js = gim.pid.pit_angle_ref*1000;
pit_angle_fdb_js = gim.pid.pit_angle_fdb*1000;
pit_speed_ref_js = pid_pit.out*1000;
pit_speed_fdb_js = gim.sensor.pit_palstance*1000;
//satori:触发can发送任务,将yaw轴和pitch轴的速度控制输出通过can总线发送给电调
osSignalSet(can_msg_send_task_t, GIMBAL_MOTOR_MSG_SEND);
osSignalSet(shoot_task_t, SHOT_TASK_EXE_SIGNAL);
gimbal_stack_surplus = uxTaskGetStackHighWaterMark(NULL);
}
调参技巧
本来不太计划写调参技巧的,在第四章的教程中也说过,PID调参如果不采用系统辨析,或者是对系统建模然后做理论分析的话,更多就是靠经验来做的事情,各人有各人的一套调参习惯,对于各个参数的认知也不太习惯(哪怕是我和我一个队的队友也经常在调参时产生一些分期),所以我这里说的也只是我自己调参时的一些个人经验,拿出来和大家分享分享。
- 调参顺序,可以先角度后速度,也可以先速度后角度,但不管是哪种顺序,都一定要保证速度环的系数不全为0,否则相当于速度环没有在工作,始终没有任何输出提供给电机,电机一点都不会动的。
- 如果是先速度后角度的话,角度环所有系数设置为0时,相当于速度环的期望一直为0,把这个翻译成人话就是调试时,云台的角度应该用手掰到任何一个位置都能自然的停住不动,如果用手缓慢的掰动云台,应该能感受到明显有反抗的力,但是这个力的大小不会随着角度的变化而变化,而且云台的位置也是被推动着改变的。如果手掰动云台的力度变化,则用力越大,反抗的力就也越大。
- 如果是先角度后速度的话,速度环可以只给比例项赋值为1,另外两项设成0。这样做的主要目的是为了在调角度环时尽量闭环速度环内参数带来的影响。这个时候如果用手掰云台的话,除了感受到反抗的力之外,松手后云台角度应该是可以回到原来的位置的,而且手把云台掰的角度越大,反抗的力就也应该越大。
- 尽量不要来回修改两个环的参数,基本的控制变量思想还是得有,控制其他参数不变的情况下针对某一个参数进行调节,调到可能的最好情况之后再更换下一个参数调节。每次调节出的最好参数记得做下记录。
- 整个系统的最终测试一般用给角度环阶跃信号作为期望,或者冲激信号作为期望来进行测试。注意,只能给角度环阶跃输入,如果把阶跃输入给速度环的话,电机就会开始360°旋转了。
我个人的习惯一般还是先位置后速度。云台的参数调节除了和PID参数有关之外,还和控制周期,传感器反馈频率,器件热噪声大小等因素有关,有的时候其实不需要复杂的参数就能有很好的控制效果(我们上个赛季的车子云台双环都只用了比例项系数就调出了不错的控制效果),如果始终调不好的话需要去考虑一下有没有可能是其他因素导致的原因。
结语
这次主要是聊了聊双轴云台控制有关的一些东西,这个做起来其实真的不是很难,很多人容易被云台两个字给吓到,但是实际上上手了就会发现,虽然想要调的很好非常难(不然那些相机云台也不会随随便便就大几百上千的卖了),但是调到能够适应比赛的程度不会非常困难的,重点还是多调,多积累经验。