第九章(1)、异常检测
1.正态高斯分布


μ代表均值(曲线的对称轴)、σ代表标准差(曲线的宽度)
根据数据集估计:

2.密度估计
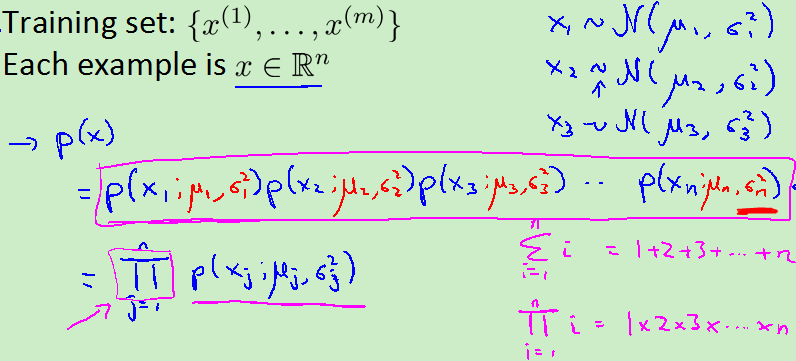

3.数据集分类
训练集使用正常产品的数据,验证集测试集使用正常和异常产品的数据。验证集和测试集的数据不能一样。

4.使用交叉验证集去求 ,因为数据是高倾斜的y=1的数据很少,所以不使用正确率来评价,而是用:
,因为数据是高倾斜的y=1的数据很少,所以不使用正确率来评价,而是用:

5.异常检测和逻辑回归的区别
异常检测:
- 正样本很少时;
- 特征很多,未来可能出现以前没有见过的正样本组合情况,数据集不能概括这些情况。
- 正态分布

异常检测和逻辑回归的不同应用:
异常检测:
- 网站欺诈检测(不正当用户,盗号):当存在经常性的非法用户时(很多),可能就要用到逻辑回归
- 产品检测
- 数据中心监控机器运行Monitoring machines
逻辑回归:
- 垃圾邮件
- 天气预测
- 癌症分类

6.数据分布
如果使用数据形成的曲线不像正态分布,可以重选数据,即使不选也可以运行很好。一般要使用log函数转换(也可以用其他的):


7.特征选择
交叉验证集的方法来选择。
另外,对于一个预测,如果异常的和正常的产品得到的p(X)值差不多,比如下图左边的情况,很可能是少了特征,比如下图右边,当加入一个新的特征后,就可以将两者区分开来:

方法:选择在异常情况下,值会变得非常大或非常小的特征。
比如数据中心监控机器运行的算法,出现了一种在本地机器死循环的的程序,然后只有CPU,带宽特征,你可以加一个(CPU/带宽)的特征,这个特征对于这个异常的值会很大。
8.多变量的高斯分布
处理情况:

密度函数:



图像:



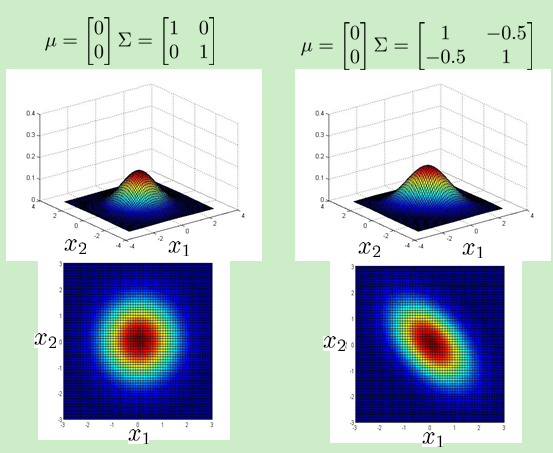
计算步骤:

9.多变量的高斯分布和原来的高斯分布区别
原高斯分布是多变量的高斯分布的一种情况:将Σ的对角线变成σi的平方,其他位置变为0,就成了原高斯分布。
原来的高斯分布:
- 用得比较多
- 效率高,比较快
- 当m较小时,仍然可用
多变量的高斯分布
- 特征之间相互有关系(原来的通过增加变量解决)
- 当m<n时,Σ的逆,可能不存在,不能用这种方法。一般m>=10*n时!确保每一个特征都能有足够的数据保证正态分布
- 求矩阵逆元,较慢,n不能太大
矩阵的逆不存在的原因:m<n;冗余特征,特征线性相关;
代码:
1.求均值和方差
function [mu sigma2] = estimateGaussian(X) [m, n] = size(X); mu = zeros(n, 1); sigma2 = zeros(n, 1); mu=mean(X); sigma2=var(X)*(m-1)/m; end
2.多变量的高斯分布
function p = multivariateGaussian(X, mu, Sigma2) k = length(mu); if (size(Sigma2, 2) == 1) || (size(Sigma2, 1) == 1)%不考虑变量之间的关系 Sigma2 = diag(Sigma2); end X = bsxfun(@minus, X, mu(:)'); p = (2 * pi) ^ (- k / 2) * det(Sigma2) ^ (-0.5) * ... exp(-0.5 * sum(bsxfun(@times, X * pinv(Sigma2), X), 2)); end
3.根据概率画等高线
function visualizeFit(X, mu, sigma2) [X1,X2] = meshgrid(0:.5:35); %二维格子 Z = multivariateGaussian([X1(:) X2(:)],mu,sigma2); %每个格子求值 Z = reshape(Z,size(X1)); plot(X(:, 1), X(:, 2),'bx'); hold on; % Do not plot if there are infinities if (sum(isinf(Z)) == 0) contour(X1, X2, Z, 10.^(-20:3:0)'); %画等高线 end hold off; end
4.选择epsilon
function [bestEpsilon bestF1] = selectThreshold(yval, pval) bestEpsilon = 0; bestF1 = 0; F1 = 0; stepsize = (max(pval) - min(pval)) / 1000; for epsilon = min(pval):stepsize:max(pval) y=(pval<=epsilon); %根据epsilon预测的y tp=sum( (y==1)&(yval==1) ); fp=sum( (y==1)&(yval==0) ); fn=sum( (y==0)&(yval==1) ); prec=tp/(tp+fp); rec=tp/(tp+fn); F1=2*prec*rec/(prec+rec); if F1 > bestF1 bestF1 = F1; bestEpsilon = epsilon; end end end
5.整体代码
clear ; close all; clc load('ex8data1.mat');%包括训练集和验证集 plot(X(:, 1), X(:, 2), 'bx'); %axis([0 30 0 30]); %xlabel('Latency (ms)'); %ylabel('Throughput (mb/s)'); [mu sigma2] = estimateGaussian(X); p = multivariateGaussian(X, mu, sigma2); %visualizeFit(X, mu, sigma2); %xlabel('Latency (ms)'); %ylabel('Throughput (mb/s)'); pval = multivariateGaussian(Xval, mu, sigma2); [epsilon F1] = selectThreshold(yval, pval); fprintf('Best epsilon found using cross-validation: %e ', epsilon); fprintf('Best F1 on Cross Validation Set: %f ', F1); outliers = find(p < epsilon); hold on plot(X(outliers, 1), X(outliers, 2), 'ro', 'LineWidth', 2, 'MarkerSize', 10); hold off