Codeforces Round #431 (Div. 2)
A 长度为偶数的一定NO，因为奇数个奇数相加不可能是偶数。
#include<bits/stdc++.h> using namespace std; #pragma comment(linker, "/STACK:102400000,102400000") #define rep(i,a,b) for (int i=a; i<=b; ++i) #define per(i,b,a) for (int i=b; i>=a; --i) #define mes(a,b) memset(a,b,sizeof(a)) #define INF 0x3f3f3f3f #define MP make_pair #define PB push_back #define fi first #define se second typedef long long ll; const int N = 200005; int n, a[N]; int main() { scanf("%d", &n); rep(i,1,n) scanf("%d", &a[i]); if((n&1) && (a[1]&1) && (a[n]&1)) puts("Yes"); else puts("No"); return 0; }
B 枚举三个点，如果有三个点在一条直线上，那这条直线一定要取，然后在这基础上再判断。
#include<bits/stdc++.h> using namespace std; #pragma comment(linker, "/STACK:102400000,102400000") #define rep(i,a,b) for (int i=a; i<=b; ++i) #define per(i,b,a) for (int i=b; i>=a; --i) #define mes(a,b) memset(a,b,sizeof(a)) #define INF 0x3f3f3f3f #define MP make_pair #define PB push_back #define fi first #define se second typedef long long ll; const int N = 1005; const double eps = 1e-6; int n; double y[N]; bool vis[N]; bool check(int a1, int a2, int a3, int a4) { double k1=(y[a1]-y[a2])/(a1-a2), k2=(y[a3]-y[a4])/(a3-a4); return fabs(k1-k2)<eps; } int main() { scanf("%d", &n); rep(i,1,n) scanf("%lf", &y[i]); if(n<=3) { double k1=(y[2]-y[1]), k2=(y[3]-y[2]); if(fabs(k1-k2)>eps) return 0*printf("Yes "); else return 0*printf("No "); } rep(l,1,3) rep(i,1,n) rep(j,1,n) { if(l==i || l==j || i==j) continue; double k1=(y[i]-y[l])/(i-l), k2=(y[j]-y[i])/(j-i); if(fabs(k1-k2)<eps) { int mi=-1; rep(j1, 1,n) if(j1!=l) { double kk=(y[j1]-y[l])/(j1-l); if(fabs(kk-k1)>eps) { vis[j1]=1; if(mi==-1) mi=j1; } } if(mi==-1) { return 0*printf("No "); } rep(j1, 1,n) if(vis[j1] && j1!=mi) { double kk=(y[j1]-y[mi])/(j1-mi); if(fabs(kk-k1)>eps) { return 0*printf("No "); } } return 0*printf("Yes "); } } if(n>=5) return 0*printf("No "); else { if(check(1,2,3,4) || check(1,3,2,4) || check(1,4,2,3)) puts("Yes"); else puts("No"); } return 0; }
C
题意：原本有一个字符串集合，初始时这个集合中的字符串都是单个字符。 操作：选出两个字符串s、t，合并为一个字符串，花费为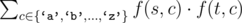 
，其中 f(s, c) 表示在字符串 s 中字符 c 的数量。 执行 n-1 次操作后变为一个字符串，这 n-1 次操作总的最小花费设为 sum。 现在给出一个数 k，要使 sum 恰好为 k，求原本的字符串集合。
tags：
考虑把不同的字符分开算。 首先如有 s 个 'a' ，最小花费是多少呢？ 稍微模拟算一下会发现就是 1+2+.....+(s-1)，即 s*(s-1)/2 。
把相同的字符都合并之后，再合并不同的字符，这时的花费都是 0 。
所以最小花费恰好为 k，那我们只要先给 'a' 字符 s 个， k剩下 k - s*(s-1)/2 ，再依次分配给 'b', 'c' ......
#include<bits/stdc++.h> using namespace std; #pragma comment(linker, "/STACK:102400000,102400000") #define rep(i,a,b) for (int i=a; i<=b; ++i) #define per(i,b,a) for (int i=b; i>=a; --i) #define mes(a,b) memset(a,b,sizeof(a)) #define INF 0x3f3f3f3f #define MP make_pair #define PB push_back #define fi first #define se second typedef long long ll; const int N = 200005; int s[N], k; int main() { int num=0; rep(i,1,1000) { s[i] = i*(i-1)/2; if(s[i]>100000) { num=i; break; } } scanf("%d", &k); if(k==0) return 0*printf("ab "); int cnt=0; while(k) { int mi = upper_bound(s+1, s+1+num, k) - s; --mi; k -= s[mi]; rep(i,1,mi) putchar('a'+cnt); ++cnt; } puts(""); return 0; }