题目我就不多说什么了,橡皮泥,一串橡皮泥哦。
非黑即白。
小明可以采取以下方法0或多次:
从某一处切割,让切割处左右队列内两条橡皮泥整个发生反转,再拼接到一起。
输入:
橡皮泥队列
输出:
最长的黑白相间的橡皮泥长度
样例输入:
bwbwb
样例输出:
5
分析:
从某一处截断之后,两边同时反转,相当于如果把每个橡皮泥比作一个球,放在一个环里,从某一处截断后,倒置环,球又滚到一起拼接起来,我还特意画了个图演示。

不知道读者看懂了没,反正我是看懂了,那我们接着往下讲。
就图上这个圆圈来说,我们来推导一个极端的情况,就是圈内所有的球球都填满了。这时候会发生什么呢?我觉得玩过这种玩具的熊孩子都应该知道,那就是——
无论你怎么插,怎么动,她都不会有一点反应。这就对了。
这是极端情况,代表的是,如果这个bw串首尾相接,那么就算小明插∞次,整个队列情况不会有丝毫改变,问题就变成了:
已知一个环形由b或w组成的串,求其中最长的bw相间的子串长。问题简单了不?
好,可能字符串首尾相接在计算机中不太好表示,其实我数据结构是真的渣,所以我还得继续简化:
对一个已知的环形队列,进行上述的“分割并反转”操作,能够包括所有分割可能的线性队列是什么样的?我们再来看图。
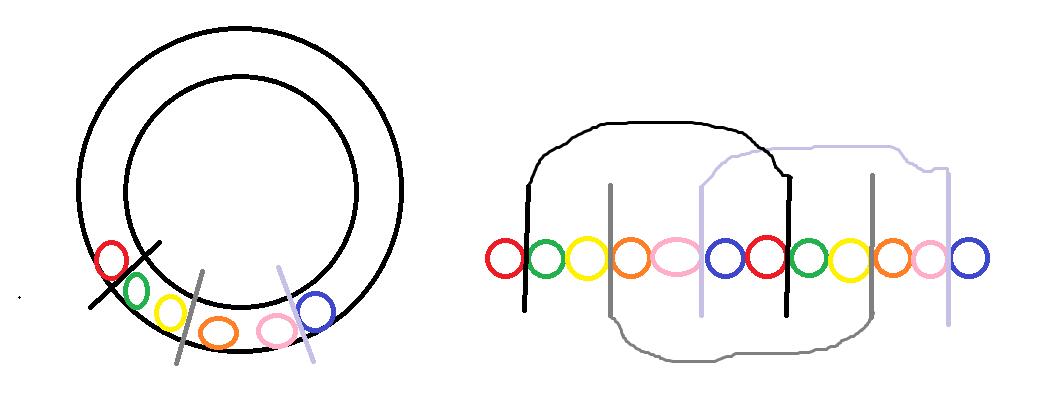
图上分别列出了三种分割后进行倒转产生的新队列。以此类推,所有的分割情况产生的新队列,无非是上图右侧队列的【一个子队列】
而上图右侧这个队列,刚好是原始队列的X2!
这样,原问题便转换为:
已知一个长为X的队列,由b或w拼接成。现求相同的两个X队列顺序拼接后,其中长为X的顺序子序列内,能出现的最长bw相间的序列长度。
源代码:
1 #include <iostream> 2 #include <string> 3 4 using namespace std; 5 6 int max(int a,int b) { 7 if (a >= b) return a; 8 else return b; 9 } 10 int main() { 11 string s; 12 cin >> s; 13 s += s; 14 int ans = 1; 15 for (int i = 0; i < s.size(); i++) { 16 int j = 1; 17 while (i != s.size() - 1 && s[i] != s[i + 1]) { 18 i++; 19 j++; 20 } 21 ans = max(ans, j); 22 } 23 if (s.size() / 2 < ans) { 24 ans = s.size() / 2; 25 } 26 printf("%d ", ans); 27 return 0; 28 }
时间复杂度:其中一个主要循环,受制参数为s.size(),所以时间复杂度为o(|S|),|S|为串长。