二叉搜索树的简单介绍

前言

本人是算法小白，java写得比较多，所以不说算法具体实现和列代码，也没那个实力，所以本文的出发点是，对算法不非常感冒的小白做个简易了解。

参考：算法导论

关于二叉搜索树

便于查找特定数据，按关键字大小构造的一棵二叉树，红黑树和B-Tree都是二叉搜索树的变形，所以二叉搜索树很关键又很容易掌握。多说无益，直接给demo

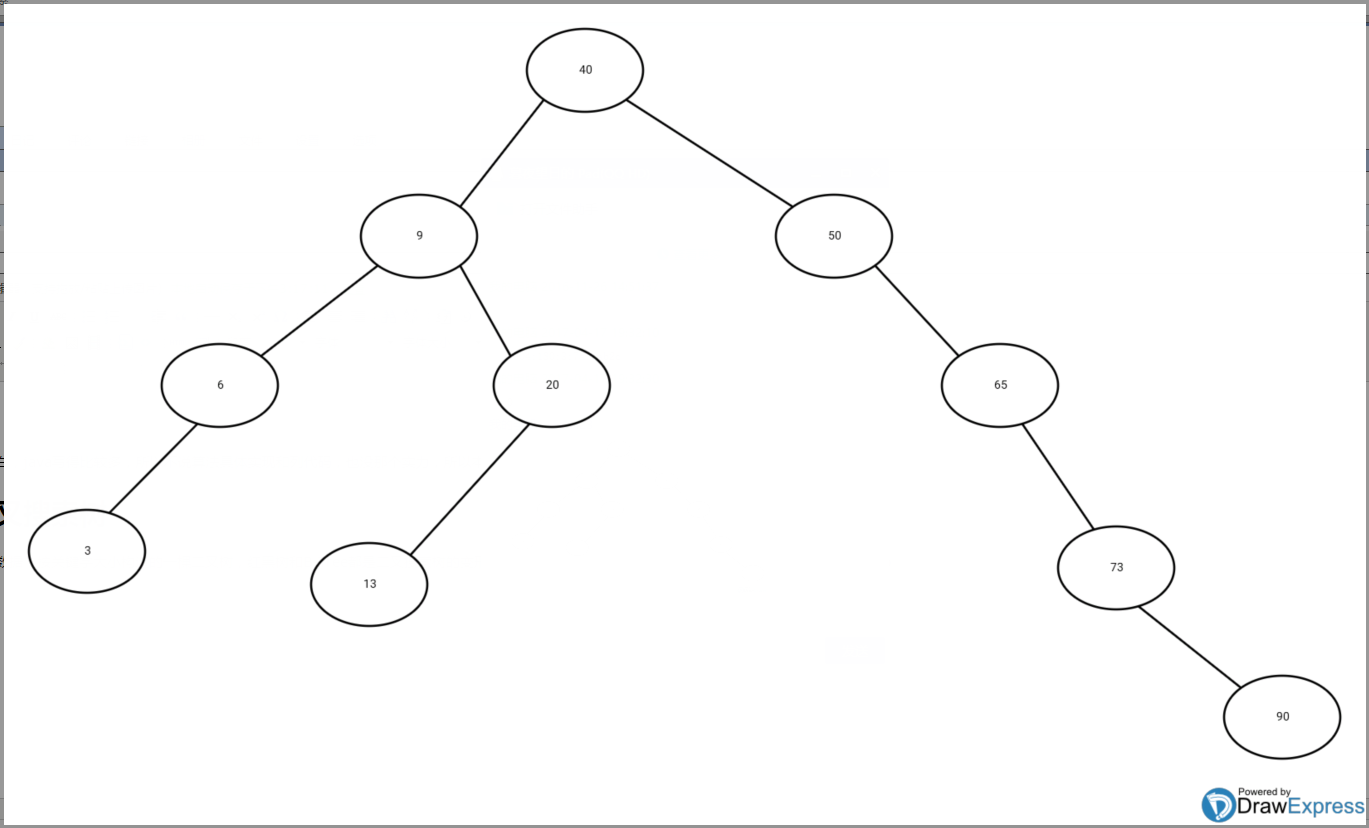
这是用一个手机软件画的（看水印就知道了），很好用，在这里给它打个小广告。

本文规约：

一个结点x，x.key代表x的关键字，x.left代表x的左孩子，x.right代表x的右孩子，x.p代表x的双亲（parent，或者叫父亲） 

特点（结构）：

这是一棵二叉搜索树，它的特点就是对于任意一个结点，其左子树中最大关键字都不超过x.key，其右子树中最小关键字都不小于x.key。这样结构很容易联想到二分法，二分法在一个有序序列找一个数效率是挺可观的。

这个特点的好处：

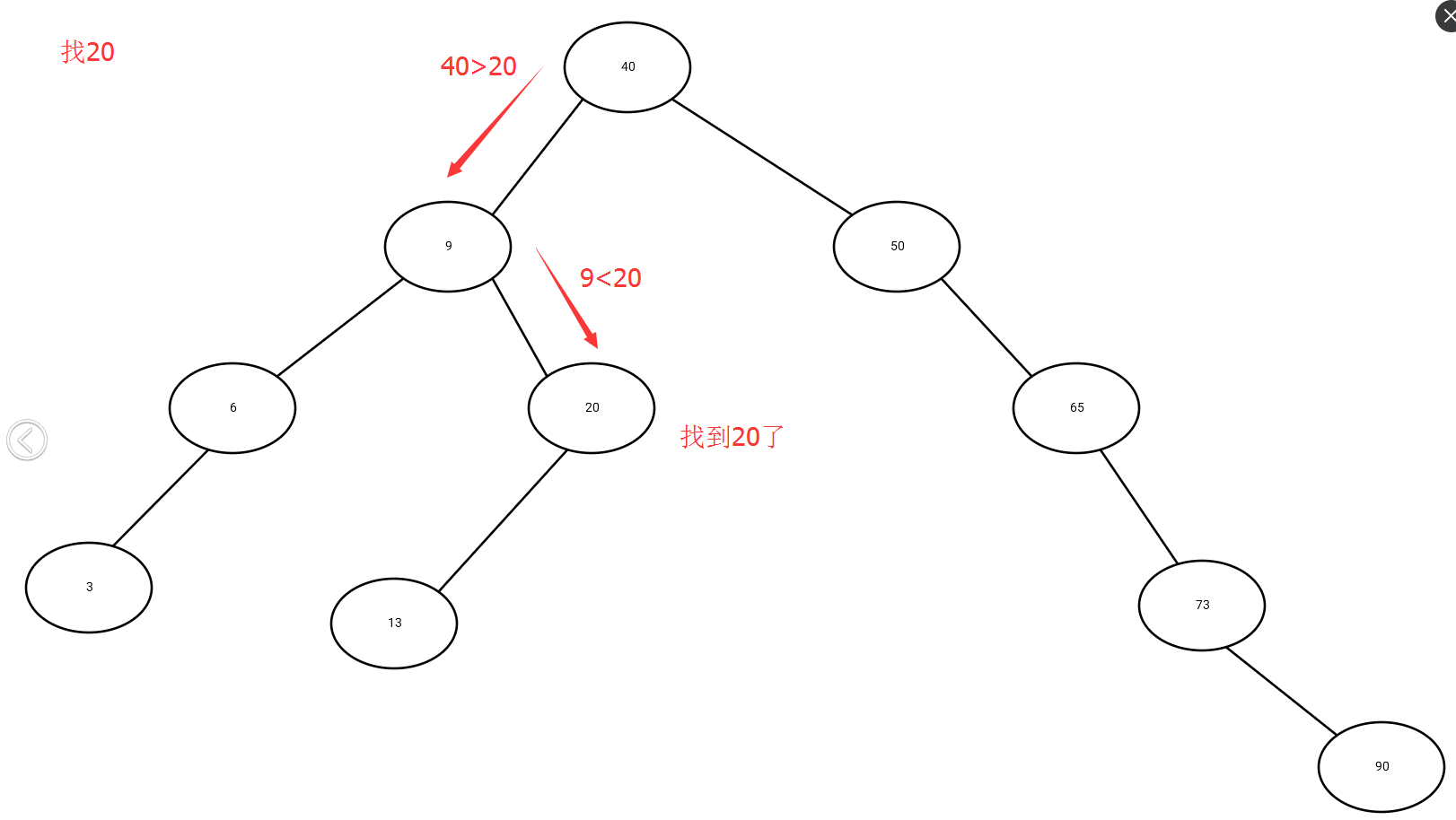
在demo中，我们要找20，就从根结点40开始，40>20，所以我们去40的左孩子9，9<20，所以去9的右孩子，20==20，找到了。当然如果找不到就返回NULL或者NIL（算法书里面用来说明该结点是空的一个特殊结点），于是乎，很容易想象到二叉搜索树的查找代码就是一个简单的递归。

缺点：

demo中如果细心就会发现这棵书的右边很臃肿，二叉搜索树的缺点便是在这里，这棵树非常不平衡，或者说数据非常极端，偏向于某一边，那么这个树的查找效率就跟遍历一个序列没什么差别，所以红黑树的目的就是让二叉搜索树近似于平衡。

有序：

因为二叉搜索树的特点，如果中序遍历这棵树，输出的序列就是所有关键字的正向排序。可以试下中序遍历demo，输出就是3，6，9，13，20，40，50，65，73，90

插入和删除：

插入：

插入比较简单，跟查找类似，一直往下，比新结点z小就往左，比z大就往右，知道遇到NULL或者NIL，就挂在那个叶子结点上。插入一直是在后面树的底插，所以二叉搜索树的根结点就是第一个插入的结点，而且不能保证这棵树是不是平衡

删除：

删除分三种情况：

1. 删除结点z没有孩子结点，直接把z从父节点断开，并用NULL或者NIL替换z
2. 如果z只有一个孩子结点，把这个孩子结点代替z就可以了
3. 如果z有两个孩子，这时候略微麻烦，先说一下什么是后继

后继：一个结点x的后继，就是关键字大于x.key的结点中最小的那个，注意这里有两种情况，如果x是有右子树，那就是x的右子树中最小那个，也就是x的右子树的最左那个结点；如果x是没有右子树，那就需要往上找，从x的父结点开始，一直往左上走（对的是左上方向），一直没有路了，那终点的父节点就是x的后继了。对于第二种情况我给个图：

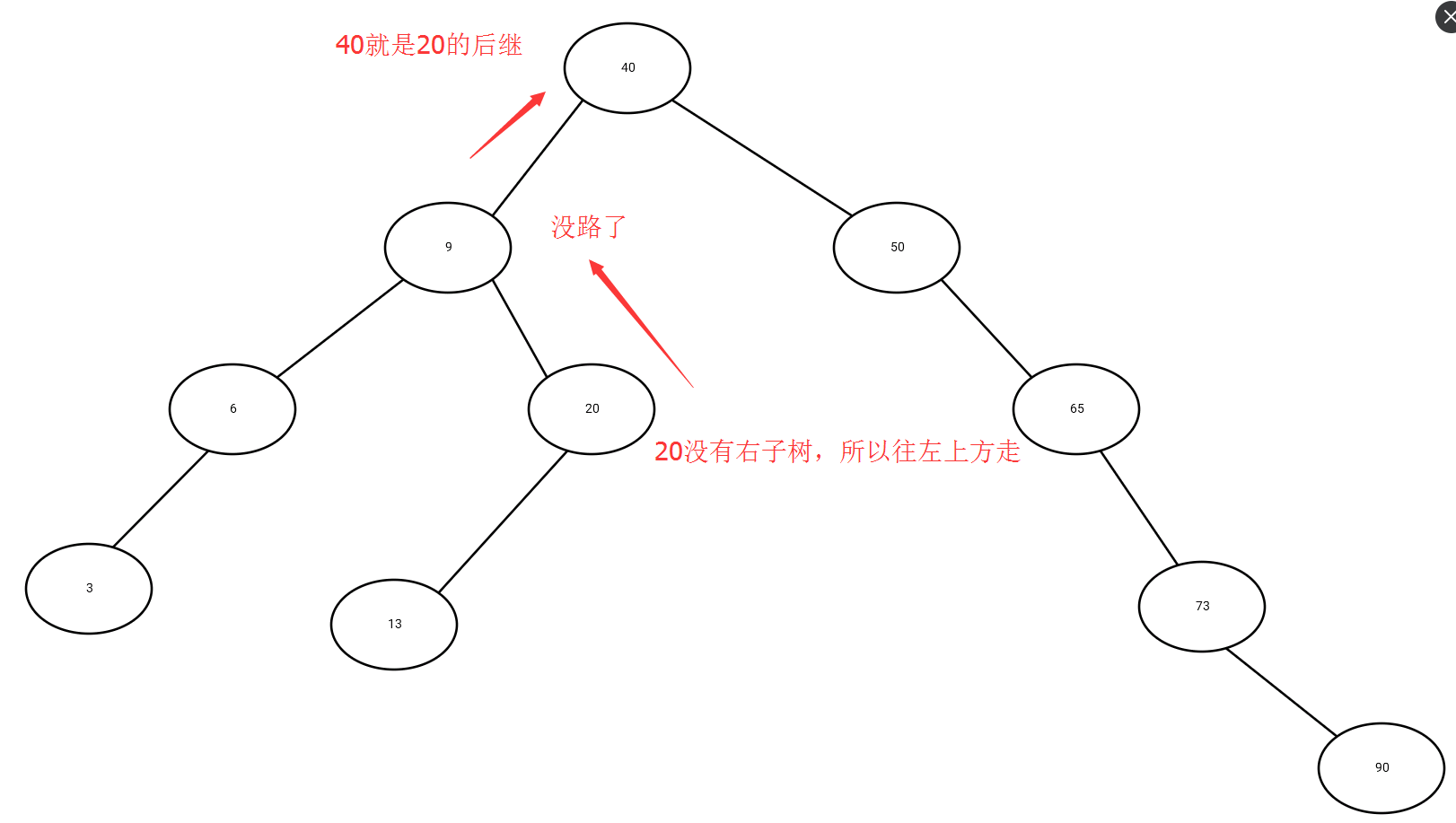
 回到刚刚删除的第三种情况，删除结点z有两个孩子，我们需要找到z的后继y（一定会在z的右子树(￣▽￣) ，额好像上面白讲了），用z的后继y代替z，z的右子树成为y的新的右子树，z的左子树称为y的新的左子树。这里直接上算法导论的图