线段树求矩形面积并
经典题目,poj 1151 是相同的题目。终于学了求矩形面积并,详细说一下。
首先是看小hh的线段树专题,因为找不到什么论文来看所以只好啃他的代码,啃了一个晚上,有感觉,但是不确定,只能轻轻体会到扫描线的意义。后来啃不下去了,就自己想,给想了出来,但是想出来居然是跟原始的方法不同的。所以下面说的是原始的方法(或者说是小hh代码中的方法),以及我自己想出来的一种方法,两种虽然不同,但是个人感觉本质还是差不多的,不过从效率上看,小hh的那种代码应该效率更高。另外下面给出的代码都是用线段树来模拟扫描法,其实还有更好的方法就是用DP的思想去优化,据说效率提高不是一点两点而是很多,但是还没学,学完会继续更新
分析:
1.矩形比较多,坐标也很大,所以横坐标需要离散化(纵坐标不需要),熟悉离散化后这个步骤不难,所以这里不详细讲解了,不明白的还请百度
2.重点:扫描线法:假想有一条扫描线,从左往右(从右往左),或者从下往上(从上往下)扫描过整个多边形(或者说畸形。。多个矩形叠加后的那个图形)。如果是竖直方向上扫描,则是离散化横坐标,如果是水平方向上扫描,则是离散化纵坐标。下面的分析都是离散化横坐标的,并且从下往上扫描的。
扫描之前还需要做一个工作,就是保存好所有矩形的上下边,并且按照它们所处的高度进行排序,另外如果是上边我们给他一个值-1,下边给他一个值1,我们用一个结构体来保存所有的上下边
struct segment
{
double l,r,h; //l,r表示这条上下边的左右坐标,h是这条边所处的高度
int f; //所赋的值,1或-1
}
接着扫描线从下往上扫描,每遇到一条上下边就停下来,将这条线段投影到总区间上(总区间就是整个多边形横跨的长度),这个投影对应的其实是个插入和删除线段操作。还记得给他们赋的值1或-1吗,下边是1,扫描到下边的话相当于往总区间插入一条线段,上边-1,扫描到上边相当于在总区间删除一条线段(如果说插入删除比较抽象,那么就直白说,扫描到下边,投影到总区间,对应的那一段的值都要增1,扫描到上边对应的那一段的值都要减1,如果总区间某一段的值为0,说明其实没有线段覆盖到它,为正数则有,那会不会为负数呢?是不可能的,可以自己思考一下)。
每扫描到一条上下边后并投影到总区间后,就判断总区间现在被覆盖的总长度,然后用下一条边的高度减去当前这条边的高度,乘上总区间被覆盖的长度,就能得到一块面积,并依此做下去,就能得到最后的面积
(这个过程其实一点都不难,只是看文字较难体会,建议纸上画图,一画即可明白,下面献上一图希望有帮组)
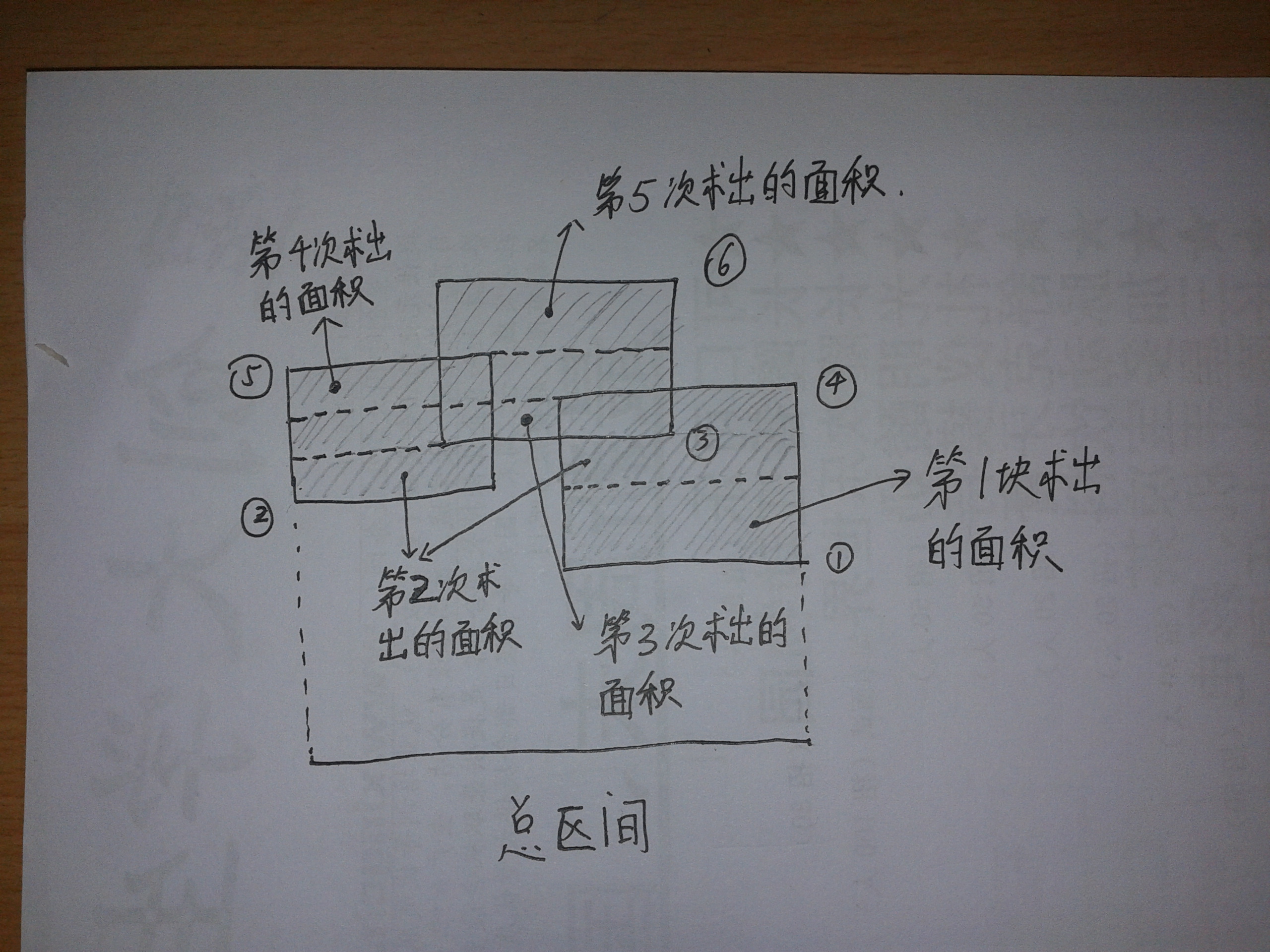
从这个图,也可以感受到,就好比一个畸形的容器,往里面倒水,从最下面往上面涨,被水淹过的部分其实就是我们要求的面积
下面给出代码
/* 1.保存矩形的上下边界,并且重要的,记录他们是属于上还是下,然后按高度升序排序 2.保存竖线坐标,并且去重,是为了离散化 3.以保存的上下边界数组去更新 */ #include <cstdio> #include <cstring> #include <algorithm> using namespace std; #define INF 0x3f3f3f3 #define MAX 110 #define LCH(i) ((i)<<1) #define RCH(i) ((i)<<1 | 1) struct segment //保存矩形上下边界 { double l,r,h; //左右横坐标,纵坐标 int f; //-1为下边界,1为上边界 }ss[2*MAX]; struct node //线段树节点 { int l,r; int cnt; //该节点被覆盖的情况 double len; //该区间被覆盖的总长度 int mid() { return (l+r)>>1; } }tt[2*MAX*4]; double pos[2*MAX]; int nums; int cmp(struct segment a ,struct segment b) { return a.h<b.h; } void build(int a, int b ,int rt) { tt[rt].l=a; tt[rt].r=b; tt[rt].cnt=0; tt[rt].len=0; if(a==b) return ; int mid=tt[rt].mid(); build(a,mid,LCH(rt)); build(mid+1,b,RCH(rt)); } int binary(double key ,int low, int high) { while(low<=high) { int mid=(low+high)>>1; if(pos[mid] == key) return mid; else if(key < pos[mid]) high=mid-1; else low=mid+1; } return -1; } void get_len(int rt) { if(tt[rt].cnt) //非0,已经被整段覆盖 tt[rt].len = pos[tt[rt].r+1] - pos[tt[rt].l]; else if(tt[rt].l == tt[rt].r) //已经不是一条线段 tt[rt].len = 0; else //是一条线段但是又没有整段覆盖,那么只能从左右孩子的信息中获取 tt[rt].len = tt[LCH(rt)].len + tt[RCH(rt)].len ; } void updata(int a, int b ,int val ,int rt) { if(tt[rt].l==a && tt[rt].r==b) //目标区间 { tt[rt].cnt += val; //更新这个区间被覆盖的情况 get_len(rt); //更新这个区间被覆盖的总长度 return ; } int mid=tt[rt].mid(); if(b<=mid) //只访问左孩子 updata(a,b,val,LCH(rt)); else if(a>mid) //只访问有孩子 updata(a,b,val,RCH(rt)); else //左右都要访问 { updata(a,mid,val,LCH(rt)); updata(mid+1,b,val,RCH(rt)); } get_len(rt); //计算该区间被覆盖的总长度 } int main() { int Case=0; int n; while(scanf("%d",&n)!=EOF && n) { nums=0; for(int i=0; i<n; i++) { double x1,y1,x2,y2; scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); ss[nums].l=x1; ss[nums].r=x2; ss[nums].h=y1; ss[nums].f=1; //记录上边界的信息 ss[nums+1].l=x1; ss[nums+1].r=x2; ss[nums+1].h=y2; ss[nums+1].f=-1; //记录下边界的信息 pos[nums]=x1; pos[nums+1]=x2; //记录横坐标 nums += 2; } sort(ss,ss+nums,cmp); //横线按纵坐标升序排序 sort(pos,pos+nums); //横坐标升序排序 //for(int i=0; i<nums; i++) printf("%.2lf %.2lf %.2lf\n",ss[i].l,ss[i].r,ss[i].h); int m=1; for(int i=1; i<nums; i++) if(pos[i]!=pos[i-1]) //去重 pos[m++]=pos[i]; build(0,m-1,1); //离散化后的区间就是[0,m-1],以此建树 double ans=0; for(int i=0; i<nums; i++) //拿出每条横线并且更新 { int l=binary(ss[i].l,0,m-1); int r=binary(ss[i].r,0,m-1)-1; updata(l,r,ss[i].f,1); //用这条线段去更新 ans += (ss[i+1].h-ss[i].h)*tt[1].len; //printf("%.2lf\n",ans); } printf("Test case #%d\n",++Case); printf("Total explored area: %.2f\n\n",ans); } return 0; }
————————————————————————————————————————————————————————————————————————————
下面说一下我自己理解出来的一个方法,当时是还没有明白上面的代码及其思想的时候想出来的
1.离散化横坐标,从下往上扫描上下边,一样要排序,一样给下边赋值1,上边赋值-1
2.没扫描到一条上下边,把它投影到总区间,但不是算总区间被覆盖的总长度。而是这条边界投影后,看这条边界对应的区间内,哪些部分对应的值变为了0(那个1和-1叠加后会变回0),变为0的部分就可以乘上高度差得到一小块的面积
这种方法还要记录一个值,就是总区间上每一段对应的最低高度,当某一段没有被线段覆盖时,它的最低高度是0,如果一旦被一个边界覆盖了,它的最低高度就是这条边界的高度(而且可以知道这个边界一定是下边界,不会是上边界首先覆盖的,这个道理和上面的一样),而已经被覆盖的线段,如果再给其他边界覆盖,无论是增加还是消除,其最低高度都不变。除非是完全消掉,那么它的最低高度又变回0
这个过程其实也不难理解的,但是文字真心难理解,建议自己画图,很容易明白,下面再献上一图,希望有帮助
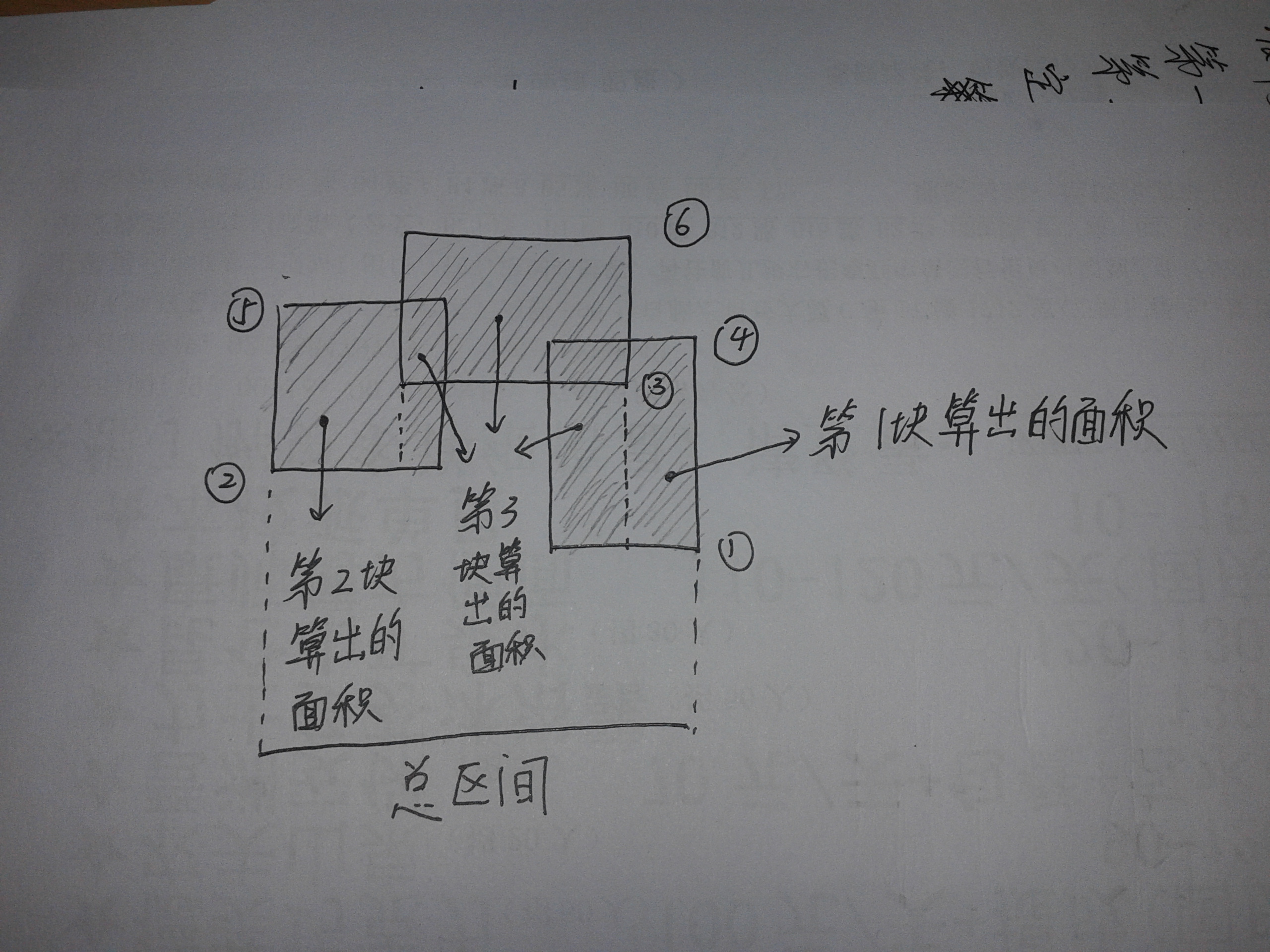
下面给出两个代码,都是实现上面的思想的,第一种用了LAZY思想,效率比第二个高,第二个是不加思索地深入到每一片叶子再求面积。但是在oj都跑出了0ms,只能说数据水了。。。
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; #define INF 0x3f3f3f3f #define MAX 110 #define LCH(i) ((i)<<1) #define RCH(i) ((i)<<1|1) struct segment { double l,r,h; int f; }ss[2*MAX]; struct node { int l,r; double h; int cnt; int mid() { return (l+r)>>1; } }tt[2*MAX*4]; double pos[2*MAX]; double ans; int nums; int cmp(struct segment a ,struct segment b) { return a.h<b.h; } void build(int a ,int b ,int rt) { tt[rt].l=a; tt[rt].r=b; tt[rt].h=0; tt[rt].cnt=INF; if(a==b) return ; int mid=tt[rt].mid(); build(a,mid,LCH(rt)); build(mid+1,b,RCH(rt)); } int binary(double key ,int low, int high) { while(low<=high) { int mid=(low+high)>>1; if(pos[mid] == key) return mid; else if(key < pos[mid]) high=mid-1; else low=mid+1; } return -1; } /* 一个线段进来,是将该线段对应的党员的值都增加val,而不是变为val 所以并不是找到目标区间就停止了,而在找到了目标区间的基础上,还要保证该区间各单元的值都相等 那么才可以成段更新,因此找到了目标区间还要继续深入(而且可知深入进去都必定是目标区间的子区间) 在最后找到了可改变值的区间时,就进去求面积函数 */ void cal(int val ,int rt ,int n) { if(tt[rt].cnt + val == 0) //可以计算面积 { ans += (pos[tt[rt].r+1]-pos[tt[rt].l])*(ss[n].h-tt[rt].h); tt[rt].cnt=0; } else if(tt[rt].cnt == 0 && val==-1) //加入底线 { tt[rt].h=ss[n].h; tt[rt].cnt=-1; } else if(tt[rt].cnt==INF) { tt[rt].cnt = val; tt[rt].h=ss[n].h; } else tt[rt].cnt+=val; return ; } void updata(int a ,int b ,int val ,int rt , int n) { int mid; if(tt[rt].l==a && tt[rt].r==b) //找到了目标区间但是还不能改变区间值 { if(tt[rt].cnt!=INF || tt[rt].l==tt[rt].r) //整段的值都是一样的,可以更新了 { cal(val,rt,n); //先进入求面积函数 } else //整段的值不同,那么还要继续深入 { mid=tt[rt].mid(); updata(a,mid,val,LCH(rt),n); updata(mid+1,b,val,RCH(rt),n); } return ; } mid=tt[rt].mid(); if(tt[rt].cnt!=INF) //当前区间的数值是统一的,要传递给左右孩子 { tt[LCH(rt)].cnt=tt[RCH(rt)].cnt=tt[rt].cnt; tt[rt].cnt=INF; } if(b<=mid) //左孩子 updata(a,b,val,LCH(rt),n); else if(a>mid) updata(a,b,val,RCH(rt),n); else { updata(a,mid,val,LCH(rt),n); updata(mid+1,b,val,RCH(rt),n); } } int main() { int Case=0; int n; while(scanf("%d",&n)!=EOF && n) { double x1,x2,y1,y2; nums=0; for(int i=0; i<n; i++) { scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); ss[nums].l=x1; ss[nums].r=x2; ss[nums].h=y1; ss[nums].f=-1; ss[nums+1].l=x1; ss[nums+1].r=x2; ss[nums+1].h=y2; ss[nums+1].f=1; pos[nums]=x1; pos[nums+1]=x2; nums += 2; } sort(ss,ss+nums,cmp); sort(pos,pos+nums); int m=1; for(int i=1; i<nums; i++) if(pos[i]!=pos[i-1]) pos[m++]=pos[i]; build(0,m-1,1); ans=0; for(int i=0; i<nums; i++) //拿出每条横线并且更新 { int l=binary(ss[i].l,0,m-1); int r=binary(ss[i].r,0,m-1)-1; updata(l,r,ss[i].f,1,i); //用这条线段去更新 //printf("%.2lf\n",ans); } printf("Test case #%d\n",++Case); printf("Total explored area: %.2lf\n\n",ans); } return 0; }
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; #define INF 0x3f3f3f3f #define MAX 110 int LCH(int n) { return n<<1; } int RCH(int n) { return n<<1|1; } struct segment { double l,r,h; int f; }ss[2*MAX]; struct node { int l,r; double h; int cnt; int mid() { return (l+r)>>1; } }tt[2*MAX*4]; double pos[2*MAX]; double ans; int nums; int cmp(struct segment a ,struct segment b) { return a.h<b.h; } void build(int a ,int b ,int rt) { tt[rt].l=a; tt[rt].r=b; tt[rt].h=0; tt[rt].cnt=0; if(a==b) return ; int mid=tt[rt].mid(); build(a,mid,LCH(rt)); build(mid+1,b,RCH(rt)); } int binary(double key ,int low, int high) { while(low<=high) { int mid=(low+high)>>1; if(pos[mid] == key) return mid; else if(key < pos[mid]) high=mid-1; else low=mid+1; } return -1; } void cal(int val ,int rt ,int n) { if(tt[rt].cnt==0 && val==-1) { tt[rt].cnt = val; tt[rt].h=ss[n].h; return ; } if(tt[rt].cnt + val == 0) { ans += (pos[tt[rt].r+1]-pos[tt[rt].l])*(ss[n].h-tt[rt].h); tt[rt].cnt=0; tt[rt].h=0; return ; } tt[rt].cnt += val; return ; } void updata(int a ,int b ,int val ,int rt ,int n) //一直更新到叶子 { if(tt[rt].l == tt[rt].r) //到达叶子 { cal(val,rt,n); return ; } int mid=tt[rt].mid(); if(b<=mid) //左孩子 updata(a,b,val,LCH(rt),n); else if(a>mid) //右孩子 updata(a,b,val,RCH(rt),n); else { updata(a,mid,val,LCH(rt),n); updata(mid+1,b,val,RCH(rt),n); } } int main() { int Case=0; int n; while(scanf("%d",&n)!=EOF && n) { double x1,x2,y1,y2; nums=0; for(int i=0; i<n; i++) { scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); ss[nums].l=x1; ss[nums].r=x2; ss[nums].h=y1; ss[nums].f=-1; ss[nums+1].l=x1; ss[nums+1].r=x2; ss[nums+1].h=y2; ss[nums+1].f=1; pos[nums]=x1; pos[nums+1]=x2; nums += 2; } sort(ss,ss+nums,cmp); sort(pos,pos+nums); int m=1; for(int i=1; i<nums; i++) if(pos[i]!=pos[i-1]) pos[m++]=pos[i]; build(0,m-1,1); ans=0; for(int i=0; i<nums; i++) //拿出每条横线并且更新 { int l=binary(ss[i].l,0,m-1); int r=binary(ss[i].r,0,m-1)-1; updata(l,r,ss[i].f,1,i); //用这条线段去更新 //printf("%.2lf\n",ans); } printf("Test case #%d\n",++Case); printf("Total explored area: %.2f\n\n",ans); } return 0; }