推荐技术公众号:不爱睡觉的大猪

本来想详细写写LCA和RMQ的东西的,但是觉得积累得还不够而且比较懒就不写了。鉴于都是超经典问题,网上和大量书籍都是很好的学习材料,所以就不想说了
这里只简单说说原理,说说代码实现上面的一些细节和注意问题,并且给出模板
下面写提供几个学习LCA和RMQ的博客,都很通熟易懂,向博主致敬
http://dongxicheng.org/structure/lca-rmq/
这个应该是讲得最好的,且博主还有很多其他文章,可以读读,感觉认真读了这篇,都不太需要看别的资料了,百度和谷歌搜索的第一位都是他,好东西大家一起学习
http://scturtle.is-programmer.com/posts/30055
这个博客讲LCA的Tarjan算法个人觉得是比较好的,我看这篇文章,看了1个小时就搞懂了LCA的Tarjan,谢谢博主。可以认真阅读,并且看懂里面附带的那个图
其余的博客,就请百度和谷歌了,能找到很多,都很好
一:LCA和RMQ是可以相互转化的
往往都只是提到了LCA可以转化为RMQ去求解,其实RMQ也能转化为LCA去求解,RMQ怎么转LCA,可以看2007年的国家队论文,里面有介绍,非常好懂。不过个人觉得,RMQ转LCA,可以学习这个思想,但是实际应用中最好不要,多此一举的感觉,求解RMQ的算法很多,不必要用LCA去求解
所以下面讲讲LCA转RMQ的实现方法(只讲实现方法,具体的原理不讲,可以看书百度,不过看了实现过程,原理大概也懂了)
LCA转RMQ算法是一个在线算法:先用时间去做预处理,然后每读入一个询问,就用很短的时间去回答它,即”问一个答一个,回答时间很短“
预备知识:LCA转为RMQ后,几乎是裸的RMQ问题,RMQ问题,这里推荐ST算法求解,如果不懂ST算法,先学习一下
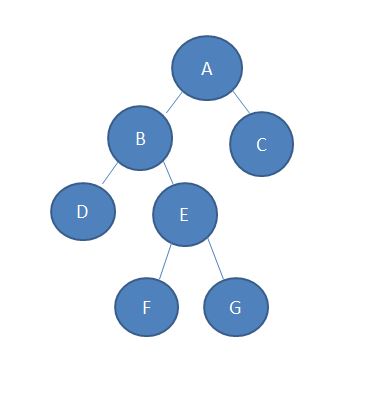
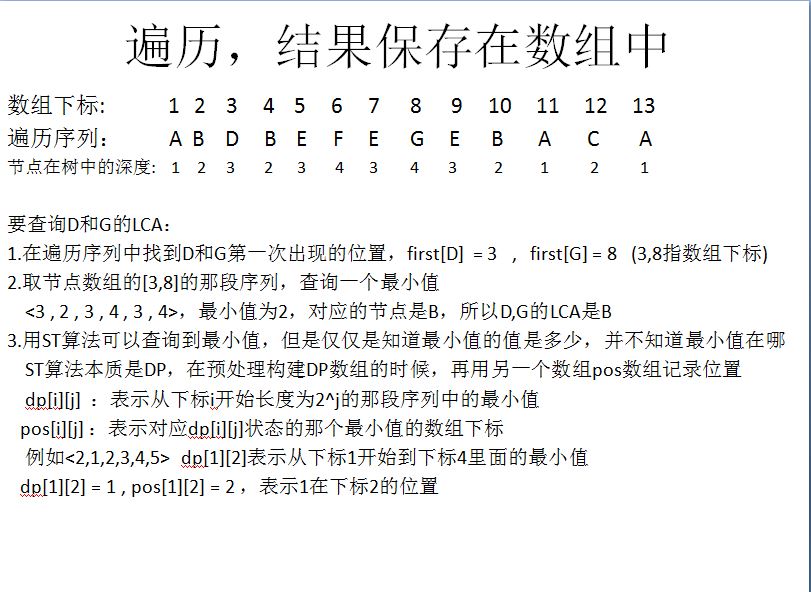


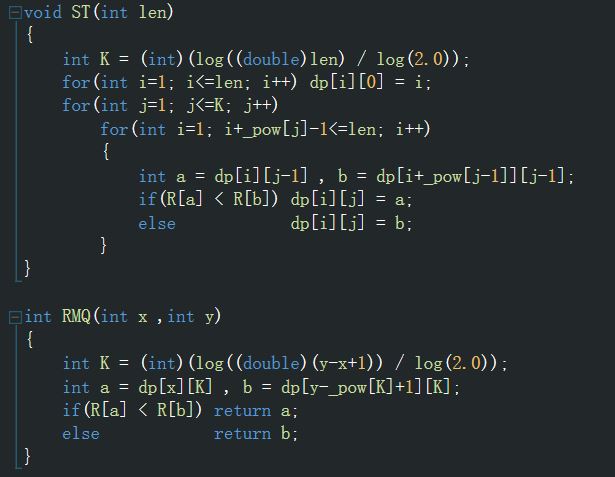
————————————————————————————————————————————————————————————
二:LCA的Tarjan算法
Tarjan算法是个离线算法:即先把所有询问保存下来,但是不回答(也回答不了),重新组织这些询问,然后再回答,但是回答的顺序,不一定是询问的顺序,即”一口气问完,处理完,再一口气回答“。如果一定要你按照询问的顺序得出答案,那么还要稍微处理一下
说说感悟:很多人说Tarjan算法强调递推的性质,我个人感觉说递推不够直接,应该说是强调时间,先后顺序。学了Tarjan几个算法,都有时间戳这个概念,这个算法里没强调这个,但是有这个意思。它定义了一个概念,什么叫处理完的节点,就是这个节点被访问了且它下面的所有子树的所有节点都被访问了,就认为这个节点是处理完了,由于是前序遍历这棵树,所以节点被处理,是有个先后顺序的,我们知道Tarjan在处理完一个节点后,就看看这个节点涉及了哪些询问,看看呗询问的另一个点是否也是被处理完的,如果另一个点也是被处理完的,那么这个询问可以被回答,否则,现在还不能回答,要等下再回答,什么时候回答,就是等到那个节点也被处理完的时候。
说说代码实现上的问题
如果理解了Tarjan,写出那个核心的dfs遍历反而不难,有时候纠结的是怎么保存询问的答案,并且按照询问的顺序,还原出答案
首先,我们是先把询问拆成两份,例如询问x和y的lca,拆成x和y的lca , y和x的lca,两者是完全相同的,等价的
对于一系列询问
1 2
1 3
2 3
3 4
变为
1 2
2 1
1 3
3 1
2 3
3 2
3 4
4 3
然后保存,保存方式是用邻接表(个人感觉这种方法比较好,可以用上位运算,记录的东西也比较少)。保存在一个表中,表的下标从0开始标号
对已表中的第k项,例如 2 3 , 那么k^1项和k项的LCA是相同的,所以就可以保存 a[k].lca = a[k^1].lca = ans
最后注意一点,Tarjan的伪代码可以很好帮助理解算法本质,注意里面一个并查集合并的操作Union(x,y)。这个Union(x,y)有好多写法,其中最简单的就是一个语句(个人推荐这种),这个Union的写法会稍微影响到dfs函数里面的写法(不影响算法本质,只是影响写法)
具体看模板
LCA转RMQ的模板
const int N = 40010; const int M = 25; int _pow[M]; //事先保存2^x,不必重复计算 int head[N]; //邻接表表头 int ver[2*N]; //保存遍历的节点序列,长度为2n-1,从下标1开始保存 int R[2*N]; //和遍历序列对应的节点深度数组,长度为2n-1,从下标1开始保存 int first[N]; //每个节点在遍历序列中第一次出现的位置 int dir[N]; //保存每个点到树根的距离,很多问题中树边都有权值,会询问两点间的距离,如果树边没权值,相当于权值为1 int dp[2*N][M]; //这个数组记得开到2*N,因为遍历后序列长度为2*n-1 bool vis[N]; //遍历时的标记数组 int tot; struct edge //保存边,数组大小至少为2*n { int u,v,w,next; }e[2*N]; void dfs(int u ,int dep) //遍历树,过程中顺便做了好多事情 { vis[u] = true; ver[++tot] = u; first[u] = tot; R[tot] = dep; for(int k=head[u]; k!=-1; k=e[k].next) if( !vis[e[k].v] ) { int v = e[k].v , w = e[k].w; dir[v] = dir[u] + w; dfs(v,dep+1); ver[++tot] = u; R[tot] = dep; } } int RMQ(int x ,int y) //这个询问仅仅是返回一个位置,即LCA所在序列数组的位置,ver[res]才是LCA的标号 { int K = (int)(log((double)(y-x+1)) / log(2.0)); int a = dp[x][K] , b = dp[y-_pow[K]+1][K]; if(R[a] < R[b]) return a; else return b; } int LCA(int u ,int v) //返回点u和点v的LCA { int x = first[u] , y = first[v]; if(x > y) swap(x,y); int res = RMQ(x,y); return ver[res]; } // lcaxy = LCA(x,y); // lcaab = LCA(a,b);
Tarjand的伪代码
void Tarjan(int u) { vis[u] = true; Make-Set(u); //以点u自己为代表元素建立一个集合,此时集合也只有它自己一个元素 ance[Find(u)] = u; //记录点u所在的那个集合的祖先是u自己,其实此时还是只有它自己 for(u的所有儿子v) if(该儿子v没有被访问) { Tarjan(v); Union(u,v); //将儿子v所在集合并在点u所在的集合,点u已经是集合的代表元素 ance[Find(u)] = u; //确保点u所在的集合的祖先是u自己 } colour[u] = true; //这个点u认为已经处理完 for(u的所有儿子v) if( colour[v] ) //儿子v也被处理完 LCA(u,v) = LCA(v,u) = ance[Find(v)]; //两者的LCA此时可以回答了,就是儿子v所在的集合的祖先 }
Tarjan模板
using namespace std; const int N = 40010; const int M = 410; int head[N]; //树边邻接表的表头 int __head[N]; //保存询问的邻接表的表头 struct edge{ //保存边 int u,v,w,next; }e[2*N]; struct ask{ //保存询问 int u,v,lca,next; }ea[M]; int dir[N]; //保存点到树根的距离 int fa[N]; //并查集,保存集合的代表元素 int ance[N]; //保存集合的组合,注意对象是集合而不是元素 bool vis[N]; //遍历时的标记数组 inline void add_edge(int u,int v,int w,int &k) //保存边 { e[k].u = u; e[k].v = v; e[k].w = w; e[k].next = head[u]; head[u] = k++; u = u^v; v = u^v; u = u^v; e[k].u = u; e[k].v = v; e[k].w = w; e[k].next = head[u]; head[u] = k++; } inline void add_ask(int u ,int v ,int &k) //保存询问 { ea[k].u = u; ea[k].v = v; ea[k].lca = -1; ea[k].next = __head[u]; __head[u] = k++; u = u^v; v = u^v; u = u^v; ea[k].u = u; ea[k].v = v; ea[k].lca = -1; ea[k].next = __head[u]; __head[u] = k++; } int Find(int x) { return x == fa[x] ? x : fa[x] = Find(fa[x]); } void Union(int u ,int v) { fa[v] = fa[u]; //可写为 fa[Find(v)] = fa[u]; } void Tarjan(int u) { vis[u] = true; ance[u] = fa[u] = u; //可写为 ance[Find(u)] = fa[u] = u; for(int k=head[u]; k!=-1; k=e[k].next) if( !vis[e[k].v] ) { int v = e[k].v , w = e[k].w; dir[v] = dir[u] + w; Tarjan(v); Union(u,v); ance[Find(u)] = u; //可写为ance[u] = u; //甚至不要这个语句都行 } for(int k=__head[u]; k!=-1; k=ea[k].next) if( vis[ea[k].v] ) { int v = ea[k].v; ea[k].lca = ea[k^1].lca = ance[Find(v)]; } } int main() { //.............省略.............. memset(head,-1,sizeof(head)); memset(__head,-1,sizeof(__head)); tot = 0; for(int i=1; i<n; i++) //建树 { int u,v,w; scanf("%d%d%d",&u,&v,&w); add_edge(u,v,w,tot); } tot = 0; for(int i=0; i<q; i++) //拆开保存询问 { int u,v; scanf("%d%d",&u,&v); add_ask(u,v,tot); } memset(vis,0,sizeof(vis)); dir[1] = 0; Tarjan(1); for(int i=0; i<q; i++) { int s = i * 2 , u = ea[s].u , v = ea[s].v , lca = ea[s].lca; //已经按顺序取出了询问和答案,lca = LCA(u,v) } return 0; }