二叉排序树(Binary Sort Tree),又称为二叉查找树(Binary Search Tree) ,即BSTree。
构造一棵二叉排序树的目的,其实并不是为了排序,而是为了提高查找和插入删除的效率。
什么是二叉排序树呢?二叉排序树具有以下几个特点。
(1)若根节点有左子树,则左子树的所有节点都比根节点小。
(2)若根节点有右子树,则右子树的所有节点都比根节点大。
(3)根节点的左,右子树也分别是二叉排序树。
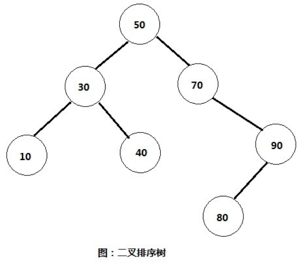
1、二叉排序树的图示
下面是二叉排序树的图示,通过它可以加深对二叉排序树的理解。
2、二叉排序树常见的操作及思路
下面是二叉排序树常见的操作及思路。
2-1、插入节点
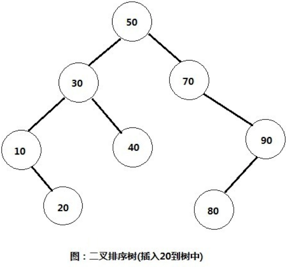
思路:比如我们要插入数字20到这棵二叉排序树中。那么步骤如下:
(1)首先将20与根节点进行比较,发现比根节点小,所以继续与根节点的左子树30比较。
(2)发现20比30也要小,所以继续与30的左子树10进行比较。
(3)发现20比10要大,所以就将20插入到10的右子树中。
此时的二叉排序树如下图:
2-2、查找节点
比如我们要查找节点10,那么思路如下:
(1)还是一样,首先将10与根节点50进行比较,发现比根节点要小,所以继续与根节点的左子树30进行比较。
(2)发现10比左子树30要小,所以继续与30的左子树10进行比较。
(3)发现两值相等,即查找成功,返回10的位置。
2-3、删除节点
删除节点的情况相对复杂,主要分为以下三种情形:
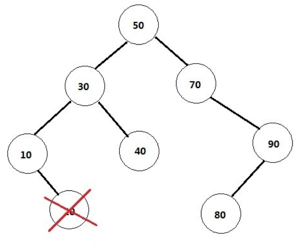
(1)删除的是叶节点(即没有孩子节点的)。比如20,删除它不会破坏原来树的结构,最简单。如图所示。
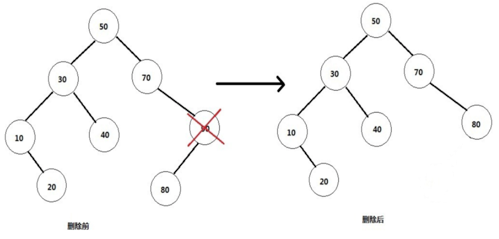
(2)删除的是单孩子节点。比如90,删除它后需要将它的孩子节点与自己的父节点相连。情形比第一种复杂一些。
(3)删除的是有左右孩子的节点。比如根节点50
这里有一个问题就是删除它后,谁将作为根节点?利用二叉树的中序遍历,就是右节点的左子树的最左孩子。

3、代码
有了思路之后,下面就开始写代码来实现这些功能。
BSTreeNode.java
public class BSTreeNode {
public int data;
public BSTreeNode left;
public BSTreeNode right;
public BSTreeNode(int data) {
this.data = data;
}
}
BSTreeOperate.java
/**
* 二叉排序树的常见操作
*/
public class BSTreeOperate {
// 树的根节点
public BSTreeNode root;
// 记录树的节点个数
public int size;
/**
* 创建二叉排序树
*
* @param list
* @return
*/
public BSTreeNode create(int[] list) {
for (int i = 0; i < list.length; i++) {
insert(list[i]);
}
return root;
}
/**
* 插入一个值为data的节点
*
* @param data
*/
public void insert(int data) {
insert(new BSTreeNode(data));
}
/**
* 插入一个节点
*
* @param bsTreeNode
*/
public void insert(BSTreeNode bsTreeNode) {
if (root == null) {
root = bsTreeNode;
size++;
return;
}
BSTreeNode current = root;
while (true) {
if (bsTreeNode.data <= current.data) {
// 如果插入节点的值小于当前节点的值,说明应该插入到当前节点左子树,而此时如果左子树为空,就直接设置当前节点的左子树为插入节点。
if (current.left == null) {
current.left = bsTreeNode;
size++;
return;
}
current = current.left;
} else {
// 如果插入节点的值大于当前节点的值,说明应该插入到当前节点右子树,而此时如果右子树为空,就直接设置当前节点的右子树为插入节点。
if (current.right == null) {
current.right = bsTreeNode;
size++;
return;
}
current = current.right;
}
}
}
/**
* 中序遍历
*
* @param bsTreeNode
*/
public void LDR(BSTreeNode bsTreeNode) {
if (bsTreeNode != null) {
// 遍历左子树
LDR(bsTreeNode.left);
// 输出节点数据
System.out.print(bsTreeNode.data + " ");
// 遍历右子树
LDR(bsTreeNode.right);
}
}
/**
* 查找节点
*/
public boolean search(BSTreeNode bsTreeNode, int key) {
// 遍历完没有找到,查找失败
if (bsTreeNode == null) {
return false;
}
// 要查找的元素为当前节点,查找成功
if (key == bsTreeNode.data) {
return true;
}
// 继续去当前节点的左子树中查找,否则去当前节点的右子树中查找
if (key < bsTreeNode.data) {
return search(bsTreeNode.left, key);
} else {
return search(bsTreeNode.right, key);
}
}
}
BSTreeOperateTest.java
public class BSTreeOperateTest {
public static void main(String[] args) {
BSTreeOperate bsTreeOperate = new BSTreeOperate();
int[] list = new int[]{50, 30, 70, 10, 40, 90, 80};
System.out.println("*********创建二叉排序树*********");
BSTreeNode bsTreeNode = bsTreeOperate.create(list);
System.out.println("中序遍历原始的数据:");
bsTreeOperate.LDR(bsTreeNode);
System.out.println("");
System.out.println("");
System.out.println("********查找节点*******");
System.out.println("元素20是否在树中:" + bsTreeOperate.search(bsTreeNode, 20));
System.out.println("");
System.out.println("********插入节点*******");
System.out.println("将元素20插入到树中");
bsTreeOperate.insert(20);
System.out.println("中序遍历:");
bsTreeOperate.LDR(bsTreeNode);
System.out.println("");
System.out.println("");
System.out.println("********查找节点*******");
System.out.println("元素20是否在树中:" + bsTreeOperate.search(bsTreeNode, 20));
System.out.println("");
}
}
运行结果:
欢迎转载,但请保留文章原始出处