基于小波分解的网格序列水印
这篇笔记是对之前的一篇论文理解的补充，论文题目为“A Blind Watermarking for 3-D Dynamic Mesh Model Using Distribution of Temporal Wavelet Coefficients”。
序列水印
这篇论文选取了序列中的一个量来进行小波分解，分解完后得到高频和低频部分（高频部分称为高频系数，低频部分称为低频系数）。作者使用低频部分来将顶点进行分组，然后修改每个分组中的高频部分，使高频部分的系数的方差满足一定能够的条件，从而嵌入水印。
对什么量进行小波分解
原始水印序列Sn，（0 <= n < N, N是总帧数）,对于原始的3D序列Sn，每一帧的重心都平移到坐标原点
序列中的每个点的坐标沿着时间轴做小波变换，即将顶点的运动轨迹看作一个信号，对这个信号做小波分解，这样Sn分解为低频部分Cn（0 <= n <= N/2 ），和高频部分Dn（0 <= n <= N/2）。
小波选取
首先需要明确的是，在小波分解中，根据选取的小波的形式不同，小波分解的结果自然也不同。我们以最简单的Haar小波分解为例，对本文中的小波分解进行阐述。下图为Haar小波的波形。
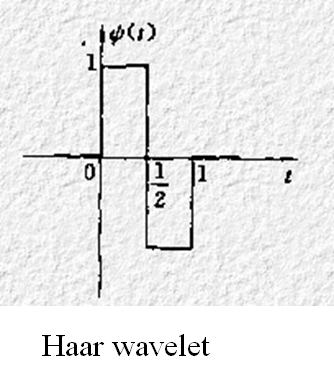
Haar小波分解
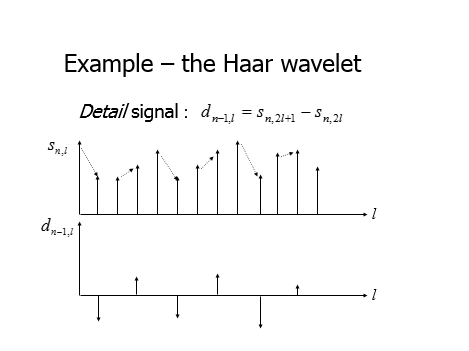
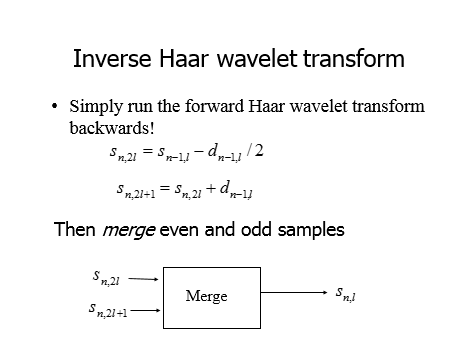
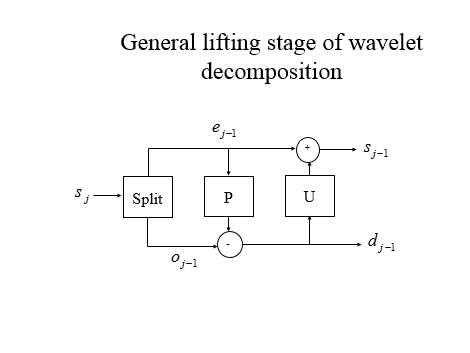
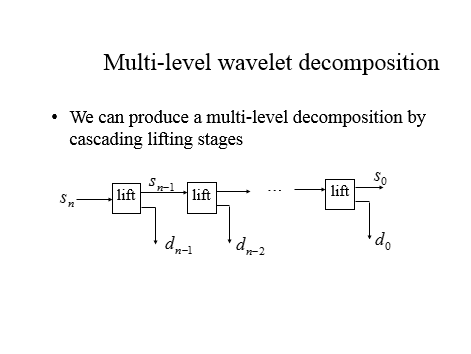
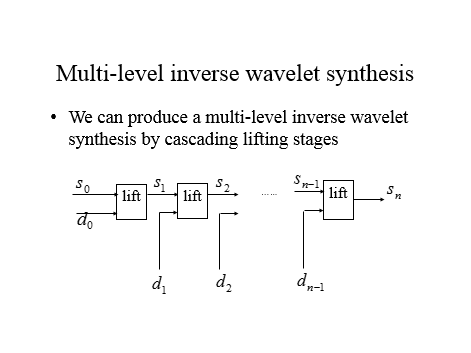
上面的英文图片来自一个ppt，不知道ppt如何加入到这个编辑器中，所以只有截图了。根据上面的描述，我们可以知道小波分解后的低频和高频分别是什么了。
对网格序列中顶点轨迹进行小波分解后，低频部分就是偶数帧的顶点坐标，而高频部分就是奇数帧的顶点坐标减去它的前一帧（偶数帧）的顶点坐标之差。
Bin的划分
得到低频部分后，求出低频部分平均帧，然后将笛卡尔坐标转换到球面坐标，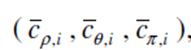
，根据p分量的大小，将顶点分到不同的bin中。例如，p的取值为[1,20],假定要嵌入的水印位数为10，那么bin的个数为10，每个bin的长度为20/10 = 2。然后按照要求修改每个bin中的高频系数，使bin中的高频系数的方差满足一定的要求，具体的做法可以参看之前的笔记，这里不再赘述。