Description
给你一棵带边权的树,有 (Q) 次修改单边边权,第一次修改前和每次修改后你需要回答树上有多少条路径 满足路径上所有边权的 gcd 为 (1)。
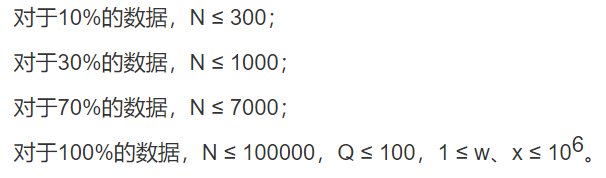
Solution
10~70pts
边分治,将重心边权分解质因数,最多只会分解出 (7) 个质因子。将这 (7) 个质因子状压,先扫左子树,设状态为每个点到重心的 gcd 是否包含这 (7) 个质因子,将每个点存入对应状态的桶中。然后扫右子树,枚举 (2^7) 种状态,累加可以配对的状态的答案。
一个菊花图就可以把这种裸边分治卡成 (10) 分,通过转二叉树+对新建的 (0) 边一通特判可以做到理论 (30) 分(我调得心态崩了然后就删了这段……)。
但数据真的是出题人拿脚造的,没转二叉树都跑 800ms 多卡过了 (70) 分范围,可惜我太傻逼,导致有一个小数据 WA 了,只得了 (60) ……
100pts
这种 gcd 题一般都和莫比乌斯反演有关。